Với giải Luyện tập 3 trang 54 Toán 8 Tập 1 Kết nối tri thức chi tiết trong Bài 11: Hình thang cân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 11: Hình thang cân
Luyện tập 3 trang 54 Toán 8 Tập 1: Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
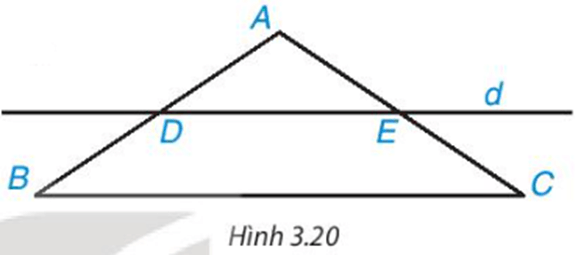
a) Tứ giác DECB là hình gì?
b) Chứng minh BE = CD.
Lời giải:
a) Theo đề bài: d // BC nên DE // BC
Suy ra DECB là hình thang.
Vì tam giác ABC cân tại A nên .
Hình thang DECB có nên là hình thang cân.
b) Hình thang cân DECB có BE và CD là hai đường chéo.
Do đó BE = CD (đpcm).
Lý thuyết Tính chất của hình thang cân
+ Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.
Ví dụ 2: Cho tứ giác EFGH như hình dưới, biết
Chứng minh EF = HG.
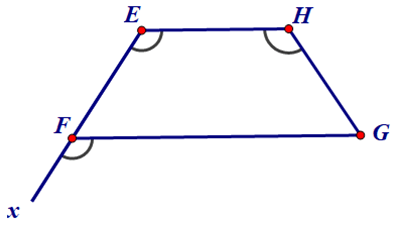
Hướng dẫn giải
Ta có: mà hai góc này ở vị trí đồng vị nên EH // FG suy ra EFGH là hình thang.
Hình thang EFGH có (hai góc kề đáy EH bằng nhau) nên EFGH là hình thang cân
EF = GH (hai cạnh bên bằng nhau).
+ Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.
Ví dụ 3: (Chứng minh Định Lí 2) Cho hình thang cân MNEF (MN // EF), chứng minh ME = NF.
Hướng dẫn giải
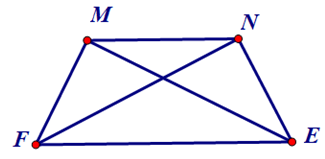
Vì MNEF (MN // EF) là hình thang cân nên và MF = NE.
Xét và có:
MF = NE
MN chung
Do đó (cạnh - góc - cạnh)
Suy ra ME = NF (cạnh tương ứng bằng nhau).
Video bài giảng Toán 8 Bài 11: Hình thang cân - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 53 Toán 8 Tập 1: Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).....
HĐ1 trang 53 Toán 8 Tập 1: Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).....
Thực hành trang 55 Toán 8 Tập 1: (H.3.22)...
Vận dụng trang 55 Toán 8 Tập 1: Hãy giải bài toán mở đầu....
Bài 3.4 trang 55 Toán 8 Tập 1: Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?...
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
