Với giải sách bài tập Toán 8 Bài 11: Hình thang cân sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán lớp 8 Bài 11: Hình thang cân

Giải SBT Toán 8 trang 34

Bài 3.7 trang 34 sách bài tập Toán 8 Tập 1: Tính các góc của hình thang ABCD (AB, CD là hai đáy) biết $\widehat{A}=2\widehat{D}$, $\widehat{B}=\widehat{C}+40°.$

Lời giải:

Trong hình thang ABCD có:

$\widehat{A}$ và $\widehat{D}$ là 2 góc bù nhau, $\widehat{B}$ và $\widehat{C}$ là 2 góc bù nhau.

Do đó $\widehat{A}+\widehat{D}=180°$, $\widehat{B}+\widehat{C}=180°$

Mà $\widehat{A}=2\widehat{D}$ nên $2\widehat{D}+\widehat{D}=180°$, suy ra $\widehat{D}=60°$. Do đó $\widehat{A}=2\widehat{D}=2\cdot 60°=120°.$

       $\widehat{B}=\widehat{C}+40°$ nên $\widehat{C}+40°+\widehat{C}=180°$, hay $2\widehat{C}=140°$, suy ra $\widehat{C}=70°$

Do đó $\widehat{B}=\widehat{C}+40°=70°+40°=110°$

Vậy hình thang ABCD có $\widehat{A}=120°;\widehat{B}=110°;\widehat{C}=70°;\widehat{D}=60°.$

Bài 3.8 trang 34 sách bài tập Toán 8 Tập 1: Chứng minh rằng trong hình thang có nhiều nhất hai góc tù.

Lời giải:

Xét hình thang ABCD có AB // CD

Ta có:

• $\widehat{A}$ và $\widehat{D}$ là hai góc kề với cạnh bên AD

Suy ra $\widehat{A}+\widehat{D}=180°$ nên trong hai góc đó có có quá 1 góc tù

• $\widehat{B}$ và $\widehat{C}$ là hai góc kề với cạnh bên BC

Suy ra $\widehat{B}+\widehat{C}=180°$ nên trong hai góc đó có có quá 1 góc tù

Do đó, trong bốn góc $\widehat{A};\widehat{B;}\widehat{C};\widehat{D}$ có nhiều nhất 2 góc là góc tù.

Bài 3.9 trang 34 sách bài tập Toán 8 Tập 1: Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B. Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với hai đáy).

Lời giải:

Do ∆ABC vuông cân tại đỉnh A nên $\widehat{ABC}=\widehat{ACB};$ $\widehat{A}=90°$

Xét trong ∆ABC ta có: $\widehat{ABC}+\widehat{ACB}+\widehat{A}=180°$

Nên $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{A}}{2}=\frac{180°-90°}{2}=45°.$

Do ∆BCD vuông cân tại đỉnh B nên $\widehat{BCD}=\widehat{BDC};$ $\widehat{CBD}=90°$

Xét trong ∆BCD ta có: $\widehat{BCD}+\widehat{BDC}+\widehat{CBD}=180°$

Nên $\widehat{BCD}=\widehat{BDC}=\frac{180°-\widehat{CBD}}{2}=\frac{180°-90°}{2}=45°.$

Ta có $\widehat{ABC}=45°=\widehat{BCD}$ nên AB // CD (hai góc so le trong bằng nhau).

Vậy ABCD là một hình thang với AB, CD là hai đáy; cạnh bên của hình thang đó là AC vuông góc với đáy AB nên hình thang đó là hình thang vuông.

Bài 3.10 trang 34 sách bài tập Toán 8 Tập 1: Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh đường thẳng SO đi qua trung điểm của AB, đi qua trung điểm của CD.

Lời giải:

Do ABCD là hình thang cân nên AD = BC, AC = BD, $\widehat{ADC}=\widehat{BCD}$

Xét ∆ABC và ∆BAD có

BC = AD, AC = BD, cạnh AB chung

Do đó ∆ABC = ∆BAD (c.c.c)

Suy ra $\widehat{BAC}=\widehat{ABD}$.

Từ đó OAB là tam giác cân tại O, nên OA = OB.

Ta có: OA + OC = AC; OB + OD = BD, mà OA = OB, AC = BD

Suy ra OC = OD.

Do đó O cách đều A và B; O cách đều C và D;

Do AB // CD nên $\widehat{SAB}=\widehat{SDC}$;$\widehat{SBA}=\widehat{SCD}$ (các cặp góc ở vị trí đồng vị)

Mà $\widehat{ADC}=\widehat{BCD}$ hay $\widehat{SDC}=\widehat{SCD}$ suy ra $\widehat{SAB}=\widehat{SDC}=\widehat{SBA}=\widehat{SCD}$

Suy ra SAB, SCD là các tam giác cân tại đỉnh S nên SA = SB, SC = SD

Do đó S cũng cách đều A và B, cách đều C và D.

Vậy S và O cùng nằm trên đường trung trực của AB, của CD nên đường thẳng SO đi qua trung điểm của AB, CD.

Bài 3.11 trang 34 sách bài tập Toán 8 Tập 1: Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C. Tính chu vi của hình thang đó biết rằng AD = 2 cm.

Lời giải:

Do CA là tia phân giác của $\widehat{C}$ nên $\widehat{BCA}=\widehat{ACD}$

Mà ABCD là hình thang cân nên AB // CD, suy ra $\widehat{BCA}=\widehat{ACD}$(hai góc so le trong)

Do đó, $\widehat{BAC}=\widehat{BCA}$, suy ra ∆ABC cân tại B.

Đặt $\widehat{BAC}=\alpha$ thì $\widehat{C}=2\alpha$.

Vì ABCD là hình thang cân nên $\widehat{D}=\widehat{C}=2\alpha .$

Tam giác ADC vuông tại A nên $\widehat{ADC}+\widehat{ACD}=2\alpha +\alpha =90°,$ suy ra $\alpha =30°,\widehat{D}=60°.$

Lấy điểm M thuộc cạnh huyền DC sao cho DM = AD, mà $\widehat{D}=60°$ thì AMD là tam giác đều, nên $\widehat{MAD}=60°$

Khi đó $\widehat{MAC}=\widehat{CAD}-\widehat{MAD}=90°-60°=30°$

Suy ra $\widehat{ACM}=\widehat{CAM}=30°$ nên tam giác MAC cân tại M

Do đó AM = MC, mà AM = DM = AD

Nên AM = DM = AD = MC hay DC = 2AD.

Vậy AB = BC = AD, DC = 2AD nên chu vi hình thang bằng

AB + BC + CD + AD = 5AD = 5.2 = 10 cm.

Xem thêm giải sách bài tập Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Bài 10: Tứ giác

Bài 11: Hình thang cân

Bài 12: Hình bình hành

Bài 13: Hình chữ nhật

Bài 14: Hình thoi và hình vuông

Lý thuyết Hình thang cân

1. Khái niệm hình thang

Hình thang là tứ giác có hai cạnh đối song song.

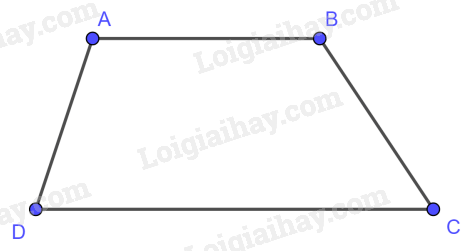
2. Khái niệm hình thang cân

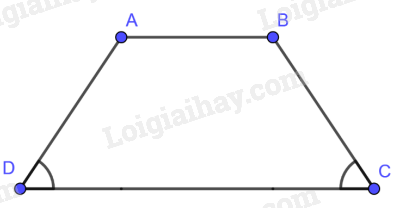
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

\

3. Tính chất của hình thang cân

Trong hình thang cân,

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau.

4. Dấu hiệu nhận biết hình thang cân

- Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.

Ví dụ:

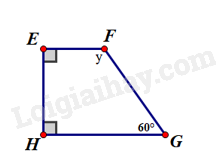
Theo định lí về tổng các góc của một tứ giác, ta có $\hat{E}+\hat{F}+\hat{G}+\hat{H}={360}^0$.

Do đó $\hat{F}=y={360}^0-{90}^0-{90}^0-{60}^0={120}^0$

Vậy $\hat{F}={120}^0$