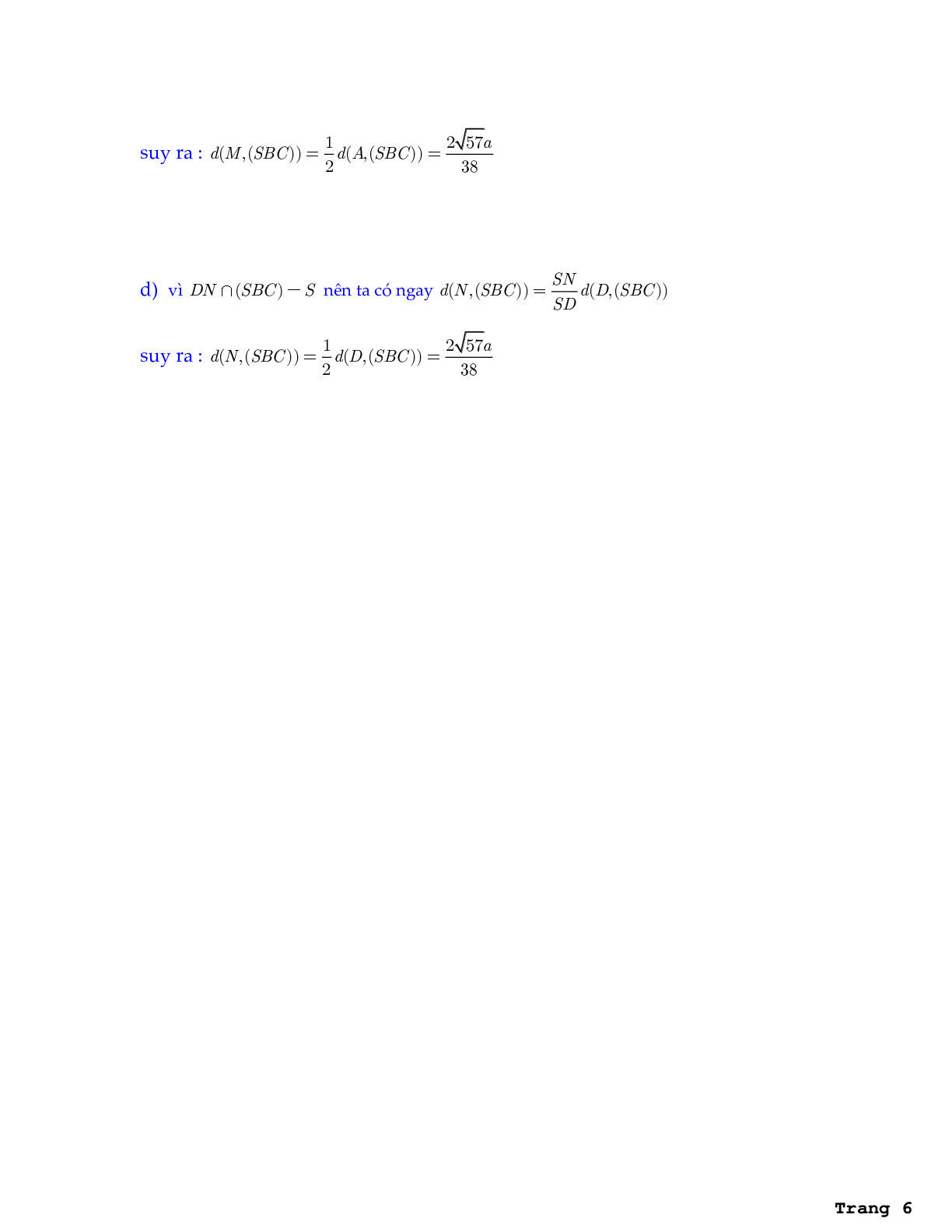Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương pháp tính nhanh khoảng cách từ điểm đến mặt phẳng, tài liệu bao gồm 6 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Phương pháp tính nhanh khoảng cách từ điểm đến mặt phẳng
A.Khoảng cách từ chân đường cao tới mặt bên của tứ diện
Xét bài toán : Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC) , tìm khoảng cách từ A tới mặt phẳng (SBC).
Giải
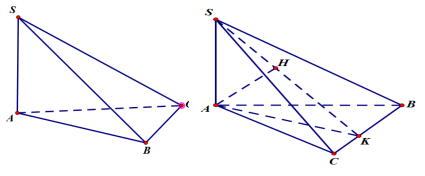
Kẻ AK vuông góc BC tại K Kẻ AH vuông góc SK tại H Thì d(A,(SBC)) = AH Tính AH
TH1 : Nếu tam giác ABC vuông tại A thì ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\]
TH2 : Nếu tam giác ABC vuông tại B ( hoặc C ) thì lúc này AK trùng với AB ( hoặc AC ):
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}}\] hoặc (\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}}\])
TH3 : Nếu tam giác ABC không vuông thì ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{d{{(A,BC)}^2}}}\]
mà d(A, BC) bằng với độ dài đường cao kẻ từ A của tam giác ABC nên ta có thể dùng diện tích hoặc các công thức lượng giác để tính độ dài đường cao
Ví dụ: Cho tam giác ABC như hình vẽ, hãy tính độ dài đường cao tam giác ABC biết độ dài các cạnh tam giác: AB = a, AC = \[a\sqrt 3 \], BC = \[a\sqrt 5 \].
Áp dụng công thức diện tích ta có:
SABC = \[\frac{1}{2}AH.BC \Rightarrow AH = \frac{{2{S_{ABC}}}}{{BC}}\]
Tính diện tích: B1: bấm
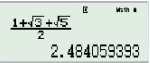
B2: bấm
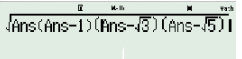
KQ: là \[\frac{{\sqrt {11} }}{4}\]vậy diện tích là \[\frac{{\sqrt {11} }}{4}\]a2.
Suy ra AH =
B.Khoảng cách từ điểm không phải là chân đường cao tới mặt bên
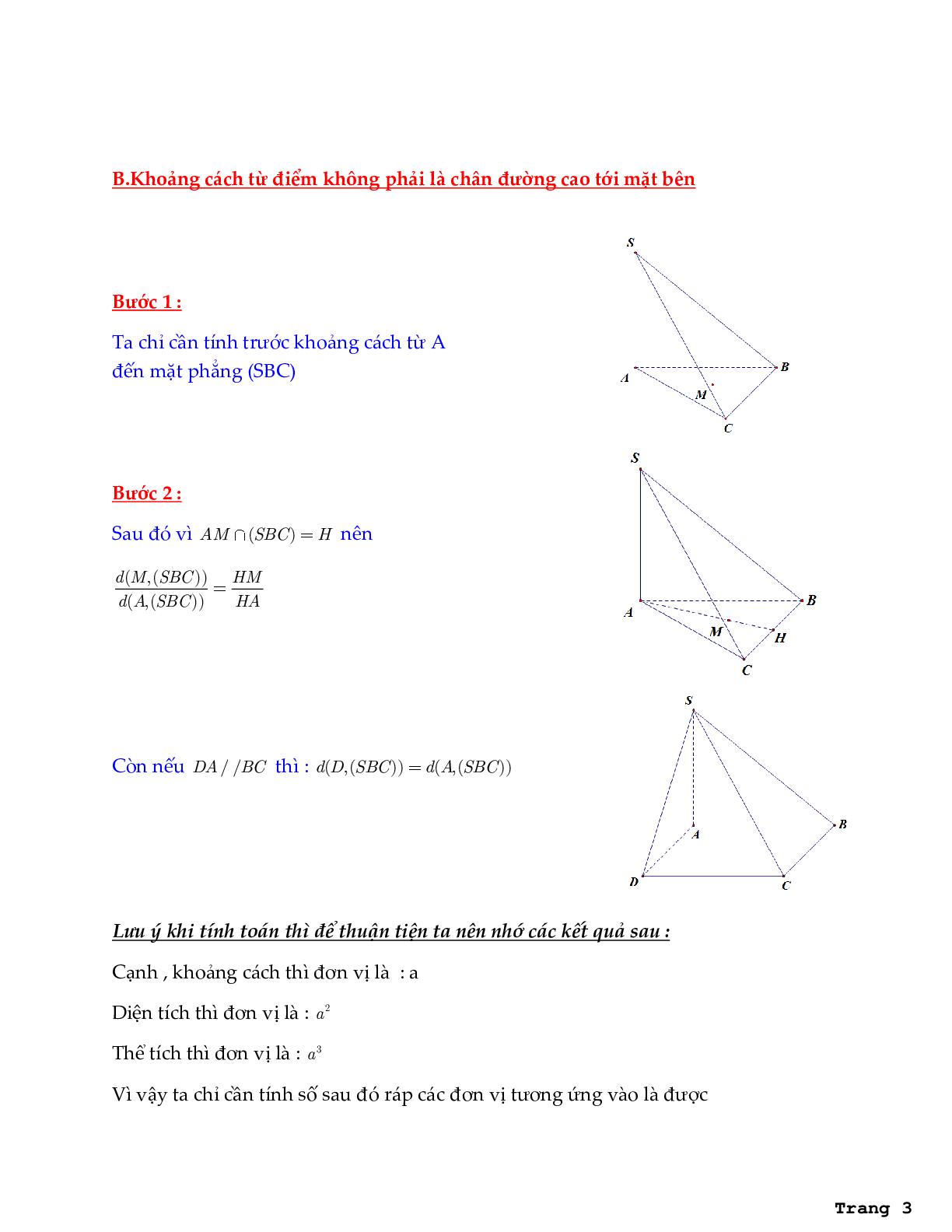
Bước 1 : Ta chỉ cần tính trước khoảng cách từ A đến mặt phẳng (SBC)
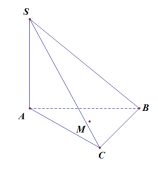
Bước 2 : Sau đó vì AM \[ \cap \](SBC) = H nên
\[\frac{{d(M,(SBC))}}{{d(A,(SBC))}} = \frac{{HM}}{{HA}}\]
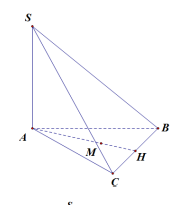
Còn nếu DA / / BC thì : d(D,(SBC)) = d(A,(SBC))
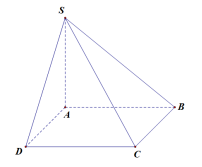
Lưu ý khi tính toán thì để thuận tiện ta nên nhớ các kết quả sau :
Cạnh , khoảng cách thì đơn vị là : a
Diện tích thì đơn vị là : a2
Thể tích thì đơn vị là : a3
Vì vậy ta chỉ cần tính số sau đó ráp các đơn vị tương ứng vào là được.
Bài Tập
Bài 1 : Cho tứ diện SABC có đáy ABC là tam giác vuông tại A , có AB = a AC =\[a\sqrt 3 \], và cạnh SA = 2a, cạnh bên SA vuông góc với đáy . Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
Giải : dễ thấy bài toán này thỏa mãn công thức 1 vì vậy ta có ngay
\[\frac{1}{{{d^2}(A,(SBC))}} = \]\[\frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\] thay (SA, AB, AC) bởi (2;1; \[\sqrt 3 \]) thì ta có ngay d(A,(SBC)) = \[\frac{{2\sqrt {57} a}}{{19}}\]
Bài 2 : Cho tứ diện SABC có đáy ABC là tam giác vuông tại B , có AB a và cạnh SA = 2a, cạnh bên SA vuông góc với đáy . Tính khoảng cách từ điểm A đến mặt phẳng (SBC) .
Giải : dễ thấy bài toán này thỏa mãn công thức 2 vì vậy ta có ngay
\[\frac{1}{{d{{(A,(SBC))}^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}}\] thay (SA, AB) bởi (2,1) thì ta có ngay \[d(A,(SBC)) = \frac{{2\sqrt 5 a}}{5}\]
Bài 3 : Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc đáy và SA=2a . Hãy tính các khoảng cách sau :
a) d(A, (SBC))
b) d(A, (SBD))
c) d(O, (SBC))
Giải : a) Dễ thấy khoảng cách này ứng với công thức 2 vì vậy ta có ngay
\[\frac{1}{{d{{(A,(SBC))}^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}}\] thay (SA, AB) bởi (2,1) thì ta có ngay \[d(A,(SBC)) = \frac{{2\sqrt 5 a}}{5}\]
b) Dễ thấy khoảng cách này ứng với công thức 1 vì vậy ra có ngay
\[\frac{1}{{d{{(A,(SBD))}^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}}\] thay (SA, AB,AC) bởi (2,1,1) thì ta có ngay \[d(A,(SBD)) = \frac{{2a}}{3}\]
c) Ta có : AO \[ \cap \] BC = C nên suy ra d(O;(SBC)) = \[\frac{1}{2}.\frac{{2\sqrt 5 a}}{5} = \frac{{\sqrt 5 a}}{5}\]
Bài 4 : Cho hình chóp SABC có đáy ABCD là hình thoi cạnh a và góc ABC = 600 , cạnh bên SA vuông góc với đáy và SA=2a , hãy tính các khoảng cách sau
a) d(A, (SBC))
b) d(D,(SBC))
c) d(M,(SBC)) với M là trung điểm của cạnh SA
d) d(N,(SBC)) với M là trung điểm của cạnh SD
Giải : Tam giác ABC cân tại B và có góc B bằng 60 độ suy ra tam giác ABC đều cạnh a
a) áp dụng công thức ở trường hợp 3 ta có ngay
\[\frac{1}{{d{{(A,(SBC))}^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{{d^2}(A,BC)}}\]
Mà: d(A,BC) = \[\frac{{\sqrt 3 a}}{2}\] ( đường cao tam giác đều )
Vậy thay (SA, d(A,BC)) bởi \[\left( {2a,\frac{{\sqrt 3 a}}{2}} \right)\] ta có ngay d(A,(SBC)) = \[\frac{{2\sqrt {57} a}}{{19}}\]
b) vì DA song song BC nên : d(A,(SBC)) = d(D,(SBC)) = \[\frac{{2\sqrt {57} a}}{{19}}\]
c) vì MA \[ \cap \](SBC) = S nên ta có ngay d(M,(SBC)) = \[\frac{{SM}}{{SA}}\]d(A,(SBC))
Suy ra: d(M,(SBC)) = \[\frac{1}{2}\]d(A,(SBC)) = \[\frac{{2\sqrt {57} a}}{{38}}\].
d) vì DN \[ \cap \](SBC) = S nên ta có ngay d(N,(SBC)) = \[\frac{{SN}}{{SD}}\] d(D,(SBC))
Suy ra d(N,(SBC)) = \[\frac{1}{2}\]d(D,(SBC)) = \[\frac{{2\sqrt {57} a}}{{38}}\]
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
