Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 20 bài tập về khoảng cách từ điểm đến mặt phẳng (dạng 1), tài liệu bao gồm 7 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

20 bài tập về khoảng cách từ điểm đến mặt phẳng (dạng 1)

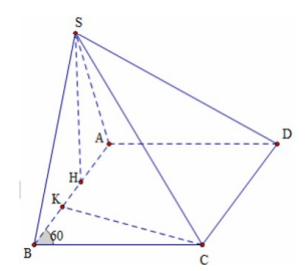
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC = 60. Mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy. Trên cạnh SC lấy điểm M sao cho MC = 2MS. Khoảng cách từ điểm M đến mặt phẳng (SAB) bằng:

A. \[\frac{a}{3}\]

B. \[\frac{{a\sqrt 3 }}{6}\]

C. \[\frac{{a\sqrt 2 }}{3}\]

D. \[\frac{{a\sqrt 3 }}{3}\]

Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với BC = \[a\sqrt 2 \], ABC = 60. Cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng:

A. \[\frac{{a\sqrt 6 }}{2}\]

B. \[\frac{{a\sqrt 2 }}{2}\]

C. \[a\sqrt 2 \]

D. \[\frac{{2a\sqrt 6 }}{3}\]

Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC = 60. Cạnh SA vuông góc với mặt phẳng đáy. Trên cạnh BC và CD lần lượt lấy hai diểm M và N sao cho MB = MC và NC = 2ND. Gọi P là giao điểm của AC và MN. Khoảng cách từ điểm P đến mặt phẳng (SAB) bằng:

A. \[\frac{{a\sqrt 3 }}{8}\]

B. \[\frac{{5a\sqrt 3 }}{{12}}\]

C. \[\frac{{5a\sqrt 3 }}{{14}}\]

D. \[\frac{{3a\sqrt 3 }}{{10}}\]

Câu 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = \[a\sqrt 3 \]. Hình chiếu vuông góc của S trên mặt đáy là trung điểm H của cạnh AC. Biết SB = \[a\sqrt 2 \]. Tính theo a khoảng cách từ điểm H đến mặt phẳng (SAB).

A. \[\frac{{a\sqrt {21} }}{3}\]

B. \[\frac{{a\sqrt {21} }}{7}\]

C. \[\frac{{3a\sqrt {21} }}{7}\]

D. \[\frac{{7a\sqrt {21} }}{3}\]

Câu 5. Cho hình chóp S.ABCD có đáy là hình chữ nhật, diện tích tứ giác ABCD bằng \[6{a^2}\sqrt 6 \]. Cạnh SA = \[a\sqrt {\frac{{110}}{3}} \]và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng 30⁰. Khoảng cách từ điểm B đến mặt phẳng (SAC) gần nhất với giá trị nào sau đây:

A. \[\frac{{13a}}{{10}}\]

B. \[\frac{{7a}}{5}\]

C. \[\frac{{3a}}{2}\]

D. \[\frac{{8a}}{5}\]

Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD = 2AB = 2BC, CD = \[2a\sqrt 2 \]. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng

A. \[\frac{{3a\sqrt {10} }}{{10}}\]

B. \[\frac{{3a\sqrt {10} }}{5}\]

C. \[\frac{{3a\sqrt {10} }}{2}\]

D. \[\frac{{a\sqrt {10} }}{3}\]

Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD = 2AB = 2BC, CD = \[2a\sqrt 2 \]. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ trọng tâm G của tam giác SAD đến mặt phẳng (SBM) bằng

A. \[\frac{{4a\sqrt {10} }}{{15}}\]

B. \[\frac{{3a\sqrt {10} }}{5}\]

C. \[\frac{{a\sqrt {10} }}{5}\]

D. \[\frac{{3a\sqrt {10} }}{{15}}\]

Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2a², AB = \[a\sqrt 2 \], BC = 2a. Gọi M là trung điểm CD. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng

A. \[\frac{{4a\sqrt {10} }}{{15}}\]

B. \[\frac{{3a\sqrt {10} }}{5}\]

C. \[\frac{{2a\sqrt {10} }}{5}\]

D. \[\frac{{3a\sqrt {10} }}{5}\]

Câu 9. Cho hình chóp S.ABCD có đáy là hình vuông, hình chiếu vuông góc của đỉnh S lên mặt đáy trùng với trọng tâm G của tam giác ABD. Biết khoảng cách từ C đến mặt phẳng (SDG) bằng \[\sqrt 5 \] và SG = 1. Thể tích khối chóp đã cho là

A. \[\frac{{25}}{{12}}\]

B. \[\frac{4}{3}\]

C. 4

D. \[\frac{{12}}{{25}}\]

Câu 10. Cho hình chóp S. ABC có đáy ABC là tam giác đều có cạnh bằng a. Gọi M là trung điểm của AC. Hình chiếu của S trên mặt đáy là điểm H thuộc đoạn BM sao cho HM = 2HB. Khoảng cách từ điểm A đến mặt phẳng (SHC) bằng

A. \[\frac{{2a\sqrt 7 }}{{14}}\]

B. \[\frac{{a\sqrt 7 }}{{14}}\]

C. \[\frac{{3a\sqrt 7 }}{{14}}\]

D. \[\frac{{2a\sqrt 7 }}{7}\]

Câu 11. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân có AC = BC = 3a. Đường thẳng A’C tạo với đáy một góc 60⁰. Trên cạnh A’C lấy điểm M sao cho A’M = 2MC. Biết rằng A’B = \[a\sqrt {31} \]. Khoảng cách từ M đến mặt phẳng (ABB’A’) là:

A. \[\frac{{3a\sqrt 2 }}{4}\]

B. \[\frac{{4a\sqrt 2 }}{3}\]

C. \[3a\sqrt 2 \]

D. \[2a\sqrt 2 \]

Câu 12. Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD với AB = a. Hình chiếu vuông góc của đỉnh S lên mặt đáy trùng với trọng tâm của tam giác ABD. Biết SC = \[2a\sqrt 2 \] và tạo với đáy một góc 45⁰. Khoảng cách từ trung điểm của SD đến mặt phẳng (SAC) là

A. \[\frac{{a\sqrt 2 }}{3}\]

B. \[\frac{{a\sqrt 3 }}{3}\]

C. \[\frac{{2a}}{3}\]

D. \[\frac{{4\sqrt 2 a}}{3}\]

Câu 13. Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD có AD = \[a\sqrt 3 \]. Tam giác SAB là tam giác đều và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của AD, H là trung điểm của AB. Biết rằng SD = 2a. Khoảng cách từ A đến mặt phẳng (SHM) là

A. \[\frac{{a\sqrt 2 }}{4}\]

B. \[\frac{{a\sqrt 3 }}{4}\]

C. \[\frac{{a\sqrt 2 }}{2}\]

D. \[\frac{{\sqrt 3 a}}{2}\]

Câu 14. Cho khối chóp S.ABC có đáy là tam giác vuông tại A có AC = a. Tam giác SAB vuông tại S và hình chiếu vuông góc của đỉnh S trên mặt đáy là điểm H thuộc cạnh AB sao cho HB = 2HA. Biết SH = \[2a\sqrt 2 \], khoảng cách từ B đến mặt phẳng (SHC) là:

A. \[\frac{{2a}}{{\sqrt 5 }}\]

B. \[\frac{a}{{\sqrt 5 }}\]

C. \[\frac{{4a}}{{\sqrt 5 }}\]

D. \[\frac{{3a}}{{\sqrt 5 }}\]

Câu 15. Cho hình lăng trụ ABCDA’B’C’D’ có đáy là hình chữ nhật với AD = \[a\sqrt 3 \]. Tam giác A’AC vuông tại A’ và thuộc mặt phẳng vuông góc với đáy. Biết rằng A’A = \[a\sqrt 2 \]. Khoảng cách từ D’ đến mặt phẳng (A’ACC’) là

A. \[\frac{{a\sqrt 3 }}{4}\]

B. \[\frac{{a\sqrt 2 }}{2}\]

C. \[\frac{{a\sqrt 2 }}{4}\]

D. \[\frac{{\sqrt 3 a}}{2}\]

Câu 16. Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = \[a\sqrt 3 \]. Hình chiếu vuông góc của S trên mặt đáy là trung điểm H của cạnh AC. Biết SB = \[a\sqrt 2 \]. Tính theo a khoảng cách từ điểm H đến mặt phẳng (SBC).

A. \[\frac{{a\sqrt 3 }}{5}\]

B. \[\frac{{2a\sqrt 3 }}{5}\]

C. \[\frac{{a\sqrt 5 }}{5}\]

D. \[\frac{{2a\sqrt 5 }}{5}\]

Câu 17. Cho hình chóp S. ABCD có đáy ABCD là hình bình hành, cạnh AB = 2a, BC = \[2a\sqrt 2 \], OD = \[a\sqrt 3 \]. Tam giác SAB nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Gọi O là giao điểm của AC và BD. Tính khoảng cách d từ điểm O đến mặt phẳng (SAB).

A. d = a

B. d = \[a\sqrt 2 \]

C. d = \[a\sqrt 3 \]

D. d = 2a

Câu 18. Cho hình chóp S. ABCD có đáy là hình chữ nhật ABCD có AD = k.AB. Hình chiếu vuông góc của đỉnh S xuống mặt đáy H thỏa mãn HB = - 2HA. Tỷ số khoảng cách từ A đến mặt phẳng (SDh) và khoảng cách từ B đến mặt phẳng (SHC) là:

A. \[\sqrt {\frac{{4 + 9{k^2}}}{{1 + 9{k^2}}}} \]

B. \[\frac{1}{2}.\sqrt {\frac{{4 + 9{k^2}}}{{1 + 9{k^2}}}} \]

C. \[\frac{1}{2}\]

D. \[\frac{1}{{2k}}\]

Câu 19. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác ABC vuông cân tại B, điểm E thuộc BC sao cho BC = 3EC. Biết hình chiếu vuông góc của A’ lên mặt đáy trùng với trung điểm H của AB. Cạnh bên AA’ = 2a và tạo với đáy một góc 60⁰. Khoảng cách từ B đến mặt phẳng (A’HE) là

A. \[\frac{{a\sqrt {39} }}{3}\]

B. \[\frac{{3a}}{5}\]

C. \[\frac{{3a}}{4}\]

D. \[\frac{{4a}}{5}\]

Câu 20. Cho hình chóp S.ABCD có đáy là hình chữ nhạt tâm O. Tam giác SAC đều và thuộc mặt phẳng vuông góc với đáy. Biết rằng SA = 2AB = 2a, khoảng cách từ D đến mặt phẳng (Sac) là

A. \[\frac{{a\sqrt 5 }}{2}\]

B. \[\frac{{a\sqrt 3 }}{2}\]

C. \[\frac{{a\sqrt 2 }}{2}\]

D. \[\frac{a}{2}\]

Hướng dẫn giải

Câu 1: Chọn đáp án B

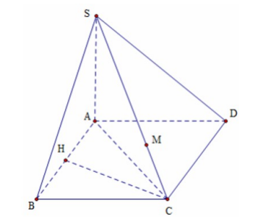
Ta có: \[\left. {\begin{array}{*{20}{c}}{(SAB) \bot (ABC)}\\{(SA{\rm{D}}) \bot (ABC)}\end{array}} \right\} \Rightarrow SA \bot (ABC{\rm{D}})\]

Dựng CH ⊥ AB \[ \Rightarrow CH \bot (SAB)\]

Do \[\frac{{d(C,(SAB))}}{{d(M,(SAB))}} = \frac{{CS}}{{MS}} = \frac{3}{2}\]

\[ \Rightarrow d(M,(SAB)) = \frac{2}{3}d(C,(SAB)) = \frac{2}{3}CH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\]

Câu 2.

Chọn đáp án A

Dựng SH ⊥ AB, do (SAB) ⊥ (ABCD) \[ \Rightarrow \]SH ⊥ (ABCD)

Dựng CK ⊥ AB, có CK ⊥ SH \[ \Rightarrow \]CK ⊥(SAB)

Do CD // AB \[ \Rightarrow \]d(D,(SAB)) = d(C,(SAB)) = CK

= BC sin60 = \[a\sqrt 2 .\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\]

Câu 3. Chọn đáp án C 

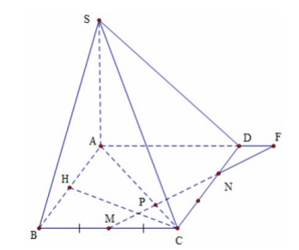
Dựng CH ⊥ AB \[ \Rightarrow \]CH ⊥ (SAB)

Giả sử MN cắt AD tại F. Theo định lý Talet ta có:

\[\frac{{DF}}{{MC}} = \frac{{ND}}{{NC}} = \frac{1}{2} \Rightarrow DF = \frac{{MC}}{2} = \frac{a}{4}\]

Khi đó \[\frac{{PA}}{{PC}} = \frac{{{\rm{AF}}}}{{MC}} = \frac{5}{2} \Rightarrow \frac{{{\rm{CA}}}}{{PA}} = \frac{7}{5}\]

Do đó d(P,(SAB)) = \[\frac{5}{7}\]d(C,(SAB)) = \[\frac{5}{7}\]CH =\[\frac{5}{7}.\frac{{a\sqrt 3 }}{2} = \frac{{5a\sqrt 3 }}{{14}}\]

Câu 4. Chọn đáp án B

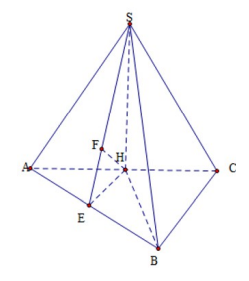
AC = \[\sqrt {A{B^2} + BC{}^2}  = 2a;BH = \frac{{AC}}{2} = a\]

Do vậy SH = \[\sqrt {S{B^2} + BH{}^2}  = a;\]dựng HE ⊥ AB; HF ⊥ SE

Ta có HE = \[\frac{{BC}}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow d(H,(SAB)) = \frac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \frac{{a\sqrt {21} }}{7}\]