Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập trắc nghiệm đường thẳng vuông góc với mặt phẳng có đáp án và lời giải, tài liệu bao gồm 67 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Dạng 1. Câu hỏi lý thuyết.

Dạng 2. Xác định quan hệ vuông góc giữa đường thẳng và mặt phẳng, đường thẳng và đường thẳng

Dạng 3. Xác định góc của đường thẳng và mặt phå̉ng .

Dạng 4. Một số bài toán liên quan khác.

Bài tập trắc nghiệm đường thẳng vuông góc với mặt phẳng có đáp án và lời giải

Đường thẳng vuông góc với mặt phẳng

A. Câu hỏi

Câu 1. Cho hai đưởng thẳng phân biệt a, b và mặt phẳng (P) , trong đó \(a \bot (P)\). Chọn mệnh đề sai.

A. Nếu \(b//a\) thì \(b//(P)\).

B. Nếu \(b//a\) thì \(b \bot (P)\).

C. Nếu \(b \bot (P)\) thì \(b//a\).

D. Nếu \(b//(P)\) thì \(b \bot a\).

Câu 2. Qua điểm O cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng \(\Delta \) cho trước?

A. Vô số.

B. 2 .

C. 3 .

D. 1 .

Câu 3. (THPT QUẢNG YÊN - QUẢNG NINH - 2018) Khẳng định nào sau đây sai?

A. Nếu đường thẳng d vuông góc với mặt phẳng \((\alpha )\) thì d vuông góc với hai đường thẳng trong mặt phẳng \((\alpha )\).

B. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong mặt phẳng \((\alpha )\) thì d vuông góc với mặt phẳng \((\alpha )\).

C. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng \((\alpha )\) thì d vuông góc với bất kỳ đường thẳng nào nằm trong mặt phẳng \((\alpha )\).

D. Nếu \(d \bot (\alpha )\) và đường thẳng \(a//(\alpha )\) thì \(d \bot a\).

Câu 4. (SỞ GD&ĐT BÌNH THUẬN - 2018) Trong không gian, khẳng định nào sau đây sai?

A. Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

D. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Câu 5. (SGD&ĐT BẮC NINH - 2018) Mệnh đề nào đúng trong các mệnh đề sau đây?

A. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì mặt phẳng (P) song song hoặc trùng với mặt phẳng (Q).

B. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì đường thẳng a song song với đường thẳng b.

C. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì đường thẳng a song song hoặc trùng với đường thẳng b.

D. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.

Câu 6. (THPT TRẦN NHÂN TÔNG - QN - LẦN 1 - 2018) Chọn mệnh đề đúng trong các mệnh đề sau đây:

A. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.

B. Cho hai đường thẳng chéo nhau a và b đồng thời \(a \bot b\). Luôn có mặt phẳng \((\alpha )\) chứa a và \((\alpha ) \bot b\).

C. Cho hai đường thẳng a và b vuông góc với nhau. Nếu mặt phẳng \((\alpha )\) chứa a và mặt phẳng \((\beta )\) chứa b thì \((\alpha ) \bot (\beta )\).

D. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.

Câu 7. (THPT BINH GIANG - HẢI DƯƠNG - 2018) Cho hai đường thẳng phân biệt a, b và mặt phẳng (P). Chọn khẳng định đúng?

A. Nếu  và \(b \bot a\) thì \(b \bot (P)\).

B. Nếu  và \(b \bot (P)\) thì \(b \bot a\).

C. Nếu \(a \bot (P)\) và \(b \bot a\) thì .

D. Nếu  và  thì .

Dạng 2. Xác định quan hệ vuông góc giữa đừơng thẳng và mặt phẳng, đường thẳng và đường thẳng

Dạng 2.1 Đường thẳng vuông góc với mặt phẳng

Câu 8. Cho tứ diện M N P Q có hai tam giác M N P và Q N P là hai tam giác cân lần lượt tại M và Q. Góc giữa hai đường thẳng MQ và NP bằng

A. ${45}^{°}$

B. ${30}^{°}$

C.${60}^{°}$

D. ${90}^{°}$

Câu 9. (TRƯỜNG THPT THANH THỦY 2018 -2019) Cho hình chóp S.ABCD có đáy là hình bình hành tâm O,SA=SC, SB=SD. Trong các khẳng định sau khẳng định nào đúng?

A. \(SA \bot (ABCD)\).

B. \(SO \bot (ABCD)\).

C. \(SC \bot (ABCD)\).

D. \(SB \bot (ABCD)\).

Câu 10. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SAvuông góc với đáy (ABCD).

Khẳng định nào sau đây sai?

A. \(CD \bot (SBC)\).

B. \(SA \bot (ABC)\).

C. \(BC \bot (SAB)\).

D. \(BD \bot (SAC)\).

Câu 11. (THPT NGUYỄN TẤT THÀNH - YÊN BÁI - 2018) Cho tứ diện ABCD có hai mặt ABC và ABD là hai tam giác đều. Gọi M là trung điểm của AB. Khẳng định nào sau đây đúng?

A. \(CM \bot (ABD)\).

B. \(AB \bot (MCD)\).

C. \(AB \bot (BCD)\).

D. \(DM \bot (ABC)\).

Câu 12. (SGD&ĐT HÀ NỘI - 2018) Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai?

A. \(BC \bot (SAB)\).

B. \(AC \bot (SBD)\).

C. \(BD \bot (SAC)\).

D. \(CD \bot (SAD)\).

Câu 13. (THPT XUÂN HÒA - VP - LẦN 1 - 2018) Cho hình chóp S,ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. Gọi H, K lần lượt là hình chiếu của A lên SC, SD. Khẳng định nào sau đây đúng?

A. \(AH \bot (SCD)\).

B. \(BD \bot (SAC)\).

C. \(AK \bot (SCD)\).

D. \(BC \bot (SAC)\).

Câu 14. (THPT NGUYẼ̃N TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Cho hình chóp S,ABCD có đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Gọi M là hình chiếu của A trên SB. Khẳng định nào sau đây là đúng?

A. \(AM \bot SD\).

B. \(AM \bot (SCD)\).

C. \(AM \bot CD\).

D. \(AM \bot (SBC)\).

Câu 15. (ĐỀ THI THỬ ĐỒNG ĐÂU-VĨNH PHÚC LẦN 01 - 2018-2019) Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với mặt phẳng đáy. Mệnh đề nào sau đây đúng?

A. \(BA \bot (SAD)\).

B. \(BA \bot (SAC)\).

C. \(BA \bot (SBC)\).

D. \(BA \bot (SCD)\).

Câu 16. Cho hình chóp S,ABCD có đáy ABCD  vuông tâm O cạnh bằng 2 , cạnh bên SA bằng 3 và vuông góc với mặt phẳng đáy. Gọi  lMà trung điểm của cạnh bên SB và N là hình chiếu vuông góc của A trên SO. Mệnh đề nào sau đây đúng?

A. \(AC \bot (SDO)\).

B. \(AM \bot (SDO)\).

C. \(SA \bot (SDO)\).

D. \(AN \bot (SDO)\).

Câu 17. (THPT HÀ HUY TẬP - HÀ TĨNH - LẦN 1 - 2018) Cho hình chóp SABC có \(SA \bot (ABC)\). Gọi H, K lần lượt là trực tâm các tam giác SBC và ABC. Mệnh đề nào sai trong các mệnh đề sau?

A. \(BC \bot (SAH)\).

B. \(HK \bot (SBC)\).

C. \(BC \bot (SAB)\).

D. S H, A K và BC đồng quy.

Dạng 2.2 Đường thẳng vuông góc với đường thẳng

Câu 18. Cho tứ diện ABCD có \(AB = AC = 2\), \(DB = DC = 3\). Khẳng định nào sau đây đúng?

A. \(BC \bot AD\).

B. \(AC \bot BD\).

C. \(AB \bot (BCD)\).

D. \(DC \bot (ABC)\).

Câu 19. (THPT CHUYÊN BẮC NINH - LẦN 1 - 2018) Cho hình chóp S.ABC đáy ABC là tam giác đều, cạnh bên SA vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AB và SB. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. \(CM \bot SB\).

B. \(CM \bot AN\).

C. \(MN \bot MC\).

D. \(AN \bot BC\).

Câu 20. (CHUYÊN LONG AN - LẦN 1 - 2018) Cho hình chóp S.ABC có \(SA \bot (ABC)\) và H là hình chiếu vuông góc của S lên BC. Hãy chọn khẳng định đúng.

A. \(BC \bot SC\).

B. \(BC \bot AH\).

C. \(BC \bot AB\).

D. \(BC \bot AC\).

Câu 21. (THPT TRẦN PHÚ - ĐÀ NẴNG - 2018) Cho tứ diện S . ABC có đáy ABC là tam giác vuông tại B và SA vuông góc với mặt phẳng (ABC). Gọi M, N lần lượt là hình chiếu vuông góc của A trên cạnh SB và SC. Khẳng định nào sau đây saii?

A. \(AM \bot SC\).

B.\(\begin{array}{*{20}{l}}{{\rm{ }}AM \bot MN}&{\rm{ }}\end{array}\)

C. \(AN \bot SB\)

D. \(SA \bot BC\).

Câu 22. (SGD&ĐT HÀ NỌI - 2018) Cho tứ diện đều ABCD có M, N lần lượt là trung điểm của các cạnh AB và CD. Mệnh đề nào sau đây sai?

A. \(MN \bot AB\).

B. \(MN \bot BD\).

C. \(MN \bot CD\).

D. \(AB \bot CD\).

Dạng 3. Xác định góc của đường thẳng và mặt phẳng

Dạng 3.1 Góc của cạnh bên với mặt phẳng

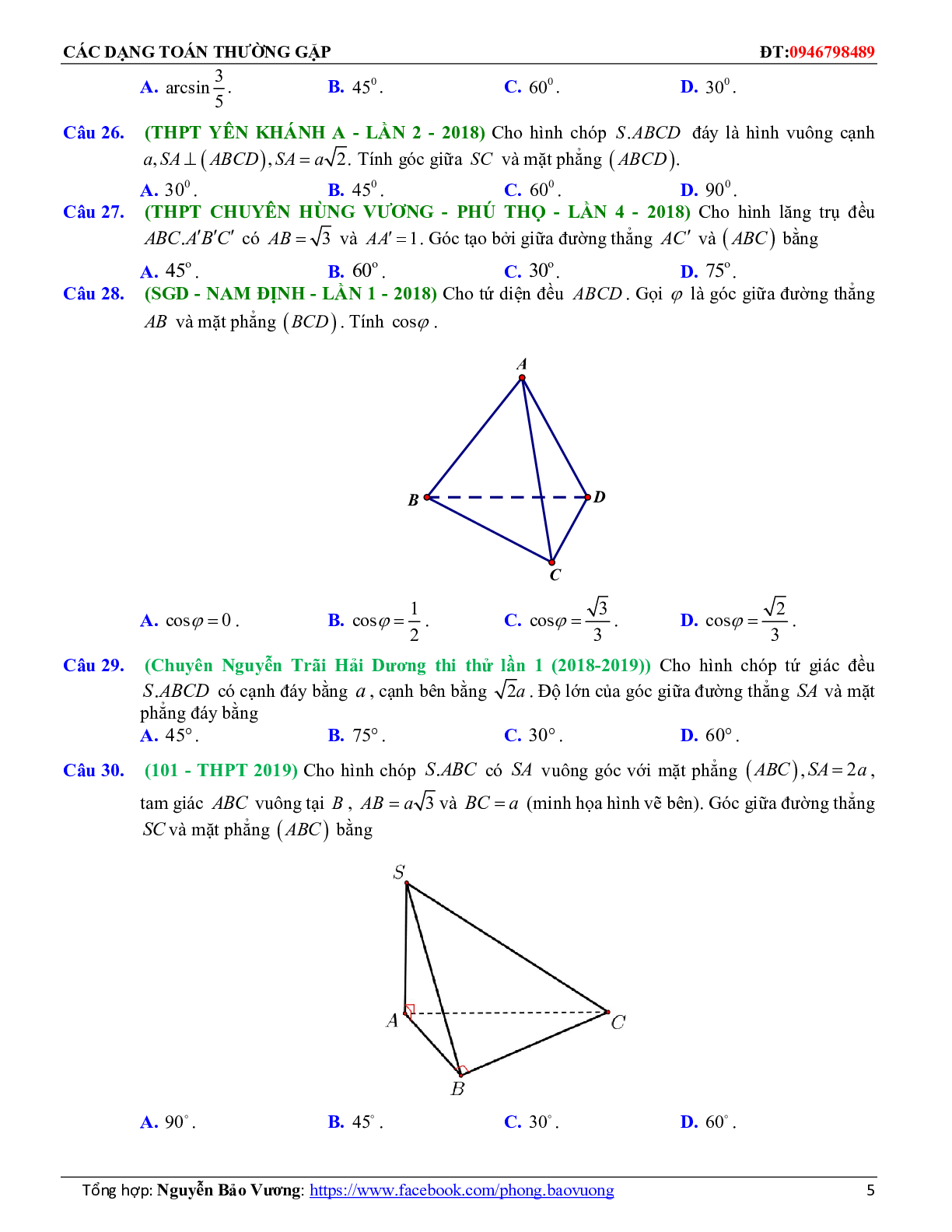
Câu 23. Cho hình chóp S.ABC có \(SA \bot (ABC);\) tam giác ABC đều cạnh a và SA=a (tham khảo hình vẽ bên). Tìm góc giữa đường thẳng SC và mặt phẳng (ABC).

A. ${60}^{°}$

B. ${45}^{°}$

C. ${135}^{°}$

D. ${90}^{°}$

Câu 24. (Trường THPT Thăng Long Lần 1 năm 2018-2019) Cho hình chóp S . A B C có cạnh SA vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng đáy là góc giữa hai đường thẳng nào dưới đây?

A. SB và AB.

B. SB và SC.

C. SA và SB.

D. SB và BC

Câu 25. Cho hình chóp S. A B C D có đáy ABCD cạnh a, SA vuông góc với đáy và \(SA = a\sqrt 3 \). Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:

A. \(\arcsin \frac{3}{5}\).

B. \({45^0}\).

C. 60⁰

D. \({30^0}\).

Câu 26. (THPT YÊN KHÁNH A - LẦN 2 - 2018) Cho hình chóp S.ABCD đáy là hình vuông cạnh \(a,SA \bot (ABCD),SA = a\sqrt 2 \). Tính góc giữa SC và mặt phẳng (ABCD).

A. ${30}^{°}$

B. ${45}^{°}$

C. ${60}^{°}$.

D. ${90}^{°}$.

Câu 27. (THPT CHUYÊN HÙNG VƯƠNG - PHÚ THỌ - LẦN 4 - 2018) Cho hình lăng trụ đều \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có \(AB = \sqrt 3 \) và \(A{A^\prime } = 1\). Góc tạo bởi giữa đường thẳng \(A{C^\prime }\) và (ABC) bằng

A. ${45}^{°}$

B. ${60}^{°}$

C. ${30}^{°}$

D. ${75}^{°}$

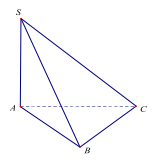
Câu 28. (SGD - NAM ĐINH - LẦN 1 - 2018) Cho tứ diện đều ABCD. Gọi \(\varphi \) là góc giữa đường thẳng AB và mặt phẳng (BCD). Tính \(\cos \varphi \).

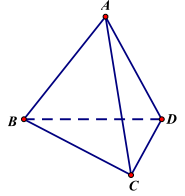
A. \(\cos \varphi  = 0\).

B. \(\cos \varphi  = \frac{1}{2}\).

C. \(\cos \varphi  = \frac{{\sqrt 3 }}{3}\).

D. \(\cos \varphi  = \frac{{\sqrt 2 }}{3}\).

Câu 29. (Chuyên Nguyễn Trãi Hải Dương thi thử lần 1 (2018-2019)) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(\sqrt 2 a\). Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng

A. ${45}^{°}$

B.$75°$

C. ${30}^{°}$

D. ${60}^{°}$

Câu 30. (101 - THPT 2019) Cho hình chóp S.ABC có SA vuông góc với mặt phẳng \((ABC),SA = 2a\), tam giác ABC vuông tại \(B,AB = a\sqrt 3 \) và \(BC = a\) (minh họa hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng

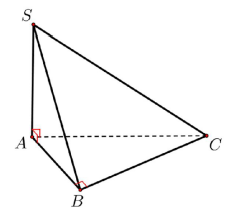
A. ${90}^{°}$

B.$45°$

C. ${30}^{°}$

D. ${60}^{°}$