Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương pháp Xác định khoảng cách từ 1 điểm đến 1 mặt phẳng toán 11 , tài liệu bao gồm 23 trang, đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Phần 1.  ĐẶT VẤN ĐỀ

       Hình học không gian là một phần quan trọng trong chương trình Toán THPT. Ở chương trình lớp 11, học sinh đã được trang bị đầy đủ các khái niệm về khoảng cách trong không gian: khoảng cách từ một điểm đến một đường thẳng, khoảng cách từ một điểm đến một mặt phẳng, khoảng cách giữa hai đường thẳng chéo nhau, khoảng cách từ một đường thẳng đến một mặt phẳng song song, khoảng cách giữa hai mặt phẳng song song. Tuy nhiên, học sinh chưa được học một cách đầy đủ các phương pháp giải các bài toán về khoảng cách nói chung và về khoảng cách từ một điểm đến một mặt phẳng nói riêng. Nhưng đây lại là một nội dung quan trọng trong các đề thi Đại học, Cao đẳng, TH chuyên nghiệp và đề thi học sinh giỏi từ trước đến nay.

Khi giải các bài toán về tính thể tích khối chóp, khối lăng trụ, chúng ta thường phải tính chiều cao của chúng, tức là phải tính khoảng cách từ một điểm đến một mặt phẳng. Một số bài toán tính khoảng cách giữa 2 mặt phẳng song song, khoảng cách từ một đường thẳng đến một mặt phẳng song song với nó, khoảng cách giữa hai đường thẳng chéo nhau cũng phải quy về khoảng cách từ một điểm đến một mặt phẳng.

Qua quá trình dạy hình học không gian lớp 11 và luyện thi Đại học, cao đẳng, tôi nhận thấy rằng, đa số các em học sinh rất lúng túng khi giải các bài toán về tính khoảng cách trong không gian và các em thường “bỏ qua” khi gặp. Nguyên nhân cơ bản là các em mới chỉ nắm được các khái niệm chứ chưa có phương pháp giải cụ thể. Vì vậy, việc trang bị đầy đủ cho học sinh các phương pháp xác định khoảng cách từ một điểm đến một mặt phẳng là điều cần thiết.

  Xuất phát từ tầm quan trọng của nội dung và từ thực trạng trên, nhằm hệ thống lại các phương pháp giải toán, tạo sự tự tin cho các em học sinh, giúp các em phát huy được khả năng phân tích, tổng hợp, khái quát hoá qua các bài tập cụ thể, với sự tích luỹ kinh nghiệm của bản thân qua những năm giảng dạy, tôi đưa ra sáng kiến kinh nghiệm “Các phương pháp xác định khoảng cách từ một điểm đến một mặt phẳng cho học sinh lớp 11". Sáng kiến kinh nghiệm này đã và đang phục vụ đắc lực cho tôi trong việc giảng dạy.

Phần 2:  GIẢI QUYẾT VẤN ĐỀ.

I. CƠ SỞ LÝ LUẬN CỦA VẤN ĐỀ.

Để giải được các bài toán về khoảng cách từ một điểm đến một mặt phẳng ta cần nắm vững các kiến thức sau:

1. Các khái niệm:

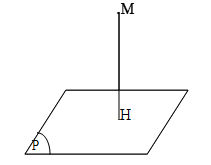
Định nghĩa 1.1: Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu vuông góc của M trên mặt phẳng (P).

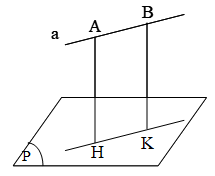
Định nghĩa 1.2: Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm nào đó của a đến (P).

2. Các tính chất:

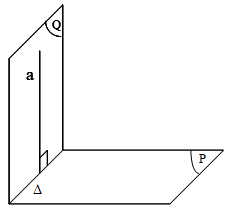
Định lý 2.1:

\[\left. \begin{array}{l}(P) \bot (Q) = \Delta \\a \subset (Q),a \bot \Delta \end{array} \right\} \Rightarrow a \bot (P)\]

Tính chất 2.2:

\[\left. \begin{array}{l}a//(P)\\A,B \in a\end{array} \right\} \Rightarrow d(A,(P)) = d(B,(P))\]

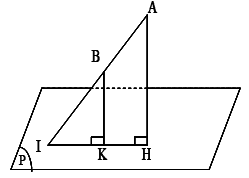
Tính chất 2.3:

\[AB \cap (P) = I \Rightarrow \frac{{d(A,(P))}}{{d(B,(P))}} = \frac{{IA}}{{IB}}\]

3. Các kiến thức của hình học phẳng:

- Các hệ thức lượng trong tam giác vuông.

- Định lý sin và định lý côsin trong tam giác.

 II. PHƯƠNG PHÁP NGHIÊN CỨU:

1. Nghiên cứu chương trình SGK THPT, nghiên cứu tài liệu về hình học không gian.

2. Thông qua hoạt động  dạy và học giáo viên hệ  thống lại tri thức cần thiết.

3. Theo dõi, đánh giá kết quả của học sinh, giáo viên đúc rút kinh nghiệm.

III. THỰC TRẠNG CỦA VẤN ĐỀ NGHIÊN CỨU. 

 - Trong chương trình THPT, do thời lượng chương trình có hạn mà phương pháp xác định khoảng cách từ một điểm đến một mặt phẳng chưa được trình bày rõ ràng, đầy đủ. Ngược lại còn rất sơ lược, chỉ mang tính chất giới thiệu qua một số bài tập đơn giản.

- Do chưa được hệ thống kiến thức và chưa được học đầy đủ các phương pháp để giải các bài toán về tính khoảng cách nên khi gặp, hầu hết học sinh thấy lúng túng và không có hướng giải.

 - Tuy nhiên, các dạng bài tập về khoảng cách thì rất phong phú, đa dạng, phức tạp và thường gặp trong các đề thi đại học, cao đẳng.

     Chính vì vậy, đa số học sinh chưa có phương pháp để giải các dạng bài tập về khoảng cách nên rất nhiều em thường "bỏ qua" khi gặp loại bài tập này.

IV. CÁC PHƯƠNG PHÁP XÁC ĐỊNH KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG.

CHƯƠNG 1

XÁC ĐỊNH KHOẢNG CÁCH TỪ ĐIỂM M ĐẾN MẶT PHẲNG (P) BẰNG CÁCH XÁC ĐỊNH HÌNH CHIẾU VUÔNG GÓC CỦA M  TRÊN (P) (PHƯƠNG PHÁP TRỰC TIẾP)

Trong không gian cho điểm M không thuộc mặt phẳng (P). Để tính khoảng cách \[d\left( {M,(P)} \right)\] từ M đến mặt phẳng (P), ta xác định hình chiếu vuông góc H của M trên mặt phẳng (P). Khi đó \[d\left( {M,(P)} \right)\]= MH

1.1    PHƯƠNG PHÁP 1: Xác định H thuộc (P) sao cho MH\[ \bot \](P)

Ví dụ 1:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, góc \[\widehat {SDA} = {30^0}\]. Các mặt bên (SAB) và (SAD) vuông góc với đáy. Tính khoảng cách từ S đến mp (ABCD).

Giải:

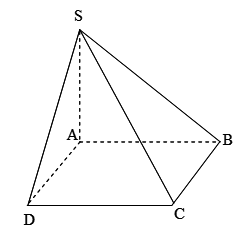
Vì (SAB) và (SAD)\[ \bot \](ABCD),

     (SAB)\[ \cap \](SAD) =SA

nên SA\[ \bot \](ABCD)

\[ \Rightarrow \]SA là khoảng cách từ S đến (ABCD)

Trong tam giác vuông SAB:

\[SA = AD.tan{30^0} = \frac{{a\sqrt 3 }}{3}\]

Nhận xét:  Hình chóp có 2 mặt kề nhau cùng vuông góc với đáy thì đường cao của hình chóp chính là giao tuyến của 2 mặt kề nhau đó.

Ví dụ 2:

Cho hình chóp S.ABC,  đáy là \[\Delta \]ABC đều cạnh a, mặt bên (SAB) vuông góc với đáy,  \[\Delta \]SAB là tam giác cân tại S, SA =2a. Tính khoảng cách từ S đến (ABC).

Giải:

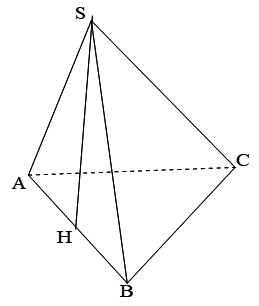
     Gọi H là trung điểm của AB.

Vì (SAB) \[ \bot \](ABC), (SAB) \[ \cap \](ABC)=AB,

SH \[ \bot \] AB ( do \[\Delta \]SAB cân, SH là trung tuyến)

nên SH\[ \bot \] (ABC).

Vậy khoảng cách từ S đến (ABC) là SH.

SH=\[\sqrt {S{A^2} - H{A^2}}  = \frac{{a\sqrt {15} }}{2}\]

Nhận xét:  Hình chóp có 1 mặt bên vuông góc với đáy thì đường cao chính là đường  vuông góc kẻ từ đỉnh xuống giao tuyến của mặt bên đó và đáy.

Ví dụ 3:

Cho hình chóp tứ giác S.ABCD, đáy ABCD là hình thoi cạnh a, tâm O; góc nhọn \[\widehat {BAD}\]=60⁰. Các cạnh bên SA=SC; SB=SD=\[a\sqrt 3 \]. Tính khoảng cách từ S đến mp (ABCD).

Giải:

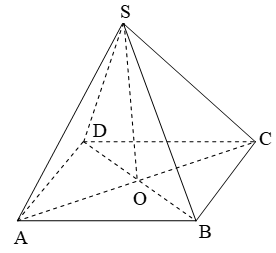
Vì SA=SC nên  cân tại S \[ \Rightarrow SO \bot AC\]

     SB=SD nên  cân tại S \[ \Rightarrow SO \bot BD\]

\[ \Rightarrow \] \[SO \bot (ABCD)\] nên SO là khoảng cách từ S

đến (ABCD)

Ta có  đều nên DB = a

          \[OB = \frac{1}{2}DB = \frac{a}{2}\]

          \[SO = \sqrt {S{B^2} - O{B^2}}  = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt {11} }}{2}\]

 Ví dụ 4:

Cho hình chóp S.ABC, BC= a, \[\widehat {BAC} = \alpha \]. Các cạnh bên SA, SB, SC cùng hợp với đáy góc \[\varphi \]. Tính  khoảng cách từ S đến mp(ABC)

Giải:

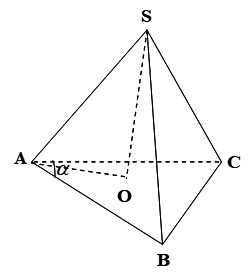
Gọi O là hình chiếu của S trên đáy ABC.

Ta có OA, OB, OC là hình chiếu của các cạnh

bên SA, SB, SC trên đáy

 \[\widehat {SAO} = \widehat {SBO} = \widehat {SCO} = \varphi \].

Các tam giác vuông SAO, SBO, SCO bằng nhau vì:

SO chung, các góc \[\widehat {SAO} = \widehat {SBO} = \widehat {SCO} = \varphi \]

\[ \Rightarrow \] OA= OB= OC.

\[ \Rightarrow \] O là tâm đường tròn ngoại tiếp \[\Delta \]ABC.

Ta có \[\frac{{BC}}{{\sin A}} = 2R \Leftrightarrow R = \frac{a}{{2\sin \alpha }}\].

Vậy d(S,(ABC)) = \[SO = OA.\tan \varphi  = \frac{{{\rm{a}}\tan \varphi }}{{2\sin \alpha }}\]

Nhận xét: Hình chóp có các cạnh bên bằng nhau hoặc các cạnh bên cùng tạo với đáy 1 góc bằng nhau thì chân đường cao chính là tâm đường tròn ngoại tiếp đáy.

Ví dụ 5:

Cho hình chóp S.ABC.  Đáy ABC là tam giác vuông tại A, BC=a, góc B=\[\alpha \]. Các mặt bên của hình chóp nghiêng đều trên đáy một góc \[\beta \]. Tính  khoảng cách từ S đến (ABC) biết hình chiếu O của S trên mp(ABC) thuộc miền trong của tam giác ABC.

Giải:  

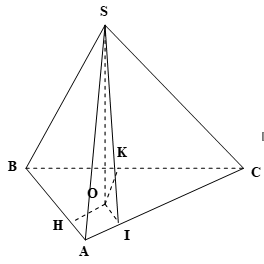
Từ O kẻ OH, OI, OK lần lượt vuông góc với

AB, AC, BC.

Do đó \[\widehat {SHO} = \widehat {SIO} = \widehat {SKO} = \beta \]

 (là góc của mặt bên và đáy)

Ta được các tam giác SOH; SOI; SOK là các tam

giác vuông tại O và bằng nhau.          

\[ \Rightarrow \]OH=OI=OK => O cách đều ba cạnh của \[\Delta ABC\],

O thuộc miền trong \[\Delta ABC\] nên O là tâm đường tròn

nội tiếp \[\Delta ABC\], bán kính r = OH = OI = OK

 với 2p=AB+CA+BC, \[AB = a\cos \alpha ,CA = {\rm{a}}\sin \alpha ,BC = a\]

\[r = \frac{{AB.AC}}{{AB + BC + CA}} = \frac{{{a^2}\sin \alpha c{\rm{os}}\alpha }}{{a(1 + \sin \alpha  + c{\rm{os}}\alpha )}}\]

Tam giác vuông SOI cho ta:

\[SO = OI\tan \beta  = r\tan \beta \]=\[\frac{{{a^2}\sin \alpha c{\rm{os}}\alpha \tan \beta }}{{a(1 + \sin \alpha  + c{\rm{os}}\alpha )}}\]

Nhận xét: Hình chóp có các mặt bên đều tạo với đáy 1 góc bằng nhau thì chân đường cao chính là tâm đường tròn nội tiếp đáy.

Chú ý:  Việc xác định hình chiếu H của M trên (P) không phải lúc nào cũng dễ dàng. Khi đó, ta có thể sử dụng định lý 2.1 (trang 2) để xác định H như sau:

1.2    PHƯƠNG PHÁP 2: Sử dụng định lý 2.1 (trang 2) để xác định hình chiếu H của M trên (P)

a)  Phương pháp:

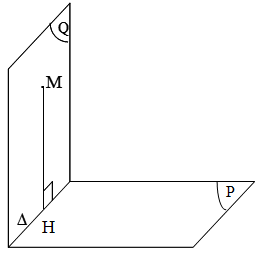
- Bước 1: Tìm mp(Q) chứa M và vuông góc với mặt phẳng (P).

- Bước 2: Xác định giao tuyến  của hai mặt phẳng (P) và (Q).

- Bước 3: Từ điểm M kẻ MH vuông góc với giao tuyến.Khi đó \(MH \bot \left( P \right)\) \[ \Rightarrow \]MH = d(M, (P)).

b) Các ví dụ:

Ví dụ 6: Cho hình chóp tứ giác S.ABCD, đáy ABCD là hình thoi cạnh a, tâm O; góc nhọn \[\widehat {BAD}\]=60⁰. Các cạnh bên SA=SC; SB=SD=\[a\sqrt 3 \]. Tính khoảng cách từ O đến mp (SBC).

Hướng dẫn:

Tìm mặt phẳng chứa O và vuông góc với (SBC)

Giải:

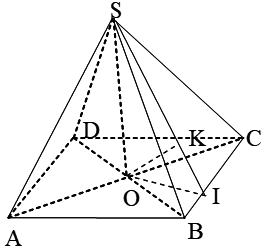
Trong mp(ABCD), kẻ OI \[ \bot \]BC (I thuộc BC).

Từ Ví dụ 3, ta có SO\[ \bot \](ABCD) nên SO\[ \bot \]BC.

\[ \Rightarrow \]BC\[ \bot \](SOI) \[ \Rightarrow \](SOI)\[ \bot \](SBC),

(SOI)\[ \cap \](SBC)=SI.

Kẻ OK \[ \bot \]SI ( K\[ \in \]SI)  thì OK\[ \bot \](SBC).

Vậy OK= d(O,(SBC)).

Từ ví dụ 3, ta có OS= \[\frac{{a\sqrt {11} }}{2}\], OB=\[\frac{a}{2}\], OI=OBsin 60⁰=\[\frac{{a\sqrt 3 }}{4}\]

Xét tam giác SOI vuông tại O có OK là đường cao:

  \[\frac{1}{{O{K^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{I^2}}}\]\[ \Leftrightarrow \]OK=\[\frac{{a\sqrt {33} }}{{2\sqrt {47} }}\]

Vậy \[d(O,(SBC)) = \frac{{a\sqrt {33} }}{{2\sqrt {47} }}\]

Ví dụ 7: (Trích: Đề thi tuyển sinh đại học khối D-2012)

Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông, tam giác A’AC vuông cân, A’C=a. Tính khoảng cách từ A đến mp(BCD’) theo a.

Hướng dẫn:

Tìm mặt phẳng chứa A và vuông góc với (BCD’)

Giải:

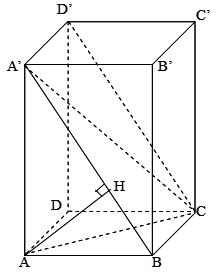
Ta có mp(BCD’) chính là mp(BCD’A’).

BC\[ \bot \]BA và BC\[ \bot \]BB’ nên BC\[ \bot \](ABB’A’)

\[ \Rightarrow \](BCD’)\[ \bot \](ABB’A’) theo giao tuyến A’B.

Kẻ AH\[ \bot \]A’B ( H\[ \in \]A’B) thì AH\[ \bot \](BCD’)

Vậy AH = d(A,(BCD’))

Tam giác A’AC vuông cân, A’C=a nên

AA’=AC=\[\frac{a}{{\sqrt 2 }}\].

Tam giác ABC vuông cân tại B nên AB=BC=\[\frac{a}{2}\].

Trong \[\Delta \]ABA’ ta có:

\[\frac{1}{{A{H^2}}} = \frac{1}{{AA{'^2}}} + \frac{1}{{A{B^2}}}\]\[ \Leftrightarrow AH = \frac{{a\sqrt 6 }}{6}\]

Vậy d(A,(BCD’)) = \[\frac{{a\sqrt 6 }}{6}\]

Ví dụ 8:

    Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a, SA vuông góc mp(ABCD), SA= \[a\sqrt 6 \].

a)    Tính khoảng cách từ A đến mp(SCD).

b)   Tính khoảng cách từ A đến mp(SBC).

 Giải:

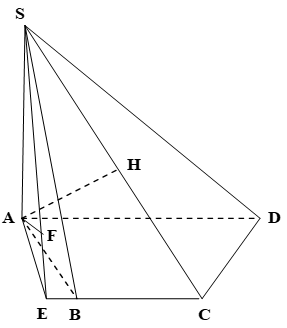
a)    Vì ABCD là nửa lục giác đều nội tiếp

trong  đường tròn đường kính AD= 2a nên

ta có AD//BC, AB= BC= CD= a

AC \[ \bot \] CD, AC= a\[\sqrt 3 \]

 Ta có:  \[\left. {\begin{array}{*{20}{c}}{CD \bot AC}\\{CD \bot SA}\end{array}} \right\}\] \[ \Rightarrow \]CD \[ \bot \] (SAC)

 \[ \Rightarrow \]  (SAC) \[ \bot \](SCD) , (SAC) \[ \cap \](SCD) = SC

Kẻ AH \[ \bot \]SC tại H thì AH \[ \bot \] (SCD).

Vậy AH= \[d\left( {A,(SCD)} \right)\]

Tam giác SAC vuông tại A có AH là đường cao nên:

\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{(a\sqrt 6 )}^2}}} + \frac{1}{{{{(a\sqrt 3 )}^2}}}\]\[ = \frac{1}{{2{a^2}}}\]

\[ \Leftrightarrow A{H^2} = 2{a^2} \Leftrightarrow AH = a\sqrt 2 \]

b)    Qua A kẻ AE \[ \bot \]BC (E thuộc BC) \[ \Rightarrow \](SAE)\[ \bot \]BC

      \[ \Rightarrow \](SAE)\[ \bot \](SBC)  mà (SAE) \[ \cap \](SBC) = AE

Qua A kẻ AF\[ \bot \]SE (F \[ \in \]SE) \[ \Rightarrow \] AF\[ \bot \](SBC).

Vậy AF =\[d\left( {A,(SBC)} \right)\].

AE = AB.sin60⁰ = \[\frac{{a\sqrt 3 }}{2}\]

Xét tam giác vuông SAE ta có:

  \[\frac{1}{{A{F^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{E^2}}} = \frac{1}{{{{(a\sqrt 6 )}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}\]=\[\frac{9}{{6{a^2}}}\]\[ \Rightarrow A{F^2} = \frac{{6{a^2}}}{9} \Rightarrow AF = \frac{{a\sqrt 6 }}{3}\]

  Vậy \[d\left( {A;(SBC)} \right)\]= \[\frac{{a\sqrt 6 }}{3}\]

Nhận xét: Trong nhiều trường hợp, việc xác định mặt phẳng (Q) chứa M và vuông góc với (P) trở nên phức tạp. Khi đó ta nên lựa chọn phương pháp gián tiếp được trình bày ở chương 2 sau đây.

CHƯƠNG 2

XÁC ĐỊNH KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG THÔNG QUA KHOẢNG CÁCH TỪ MỘT ĐIỂM KHÁC ĐẾN MẶT PHẲNG ĐÓ (PHƯƠNG PHÁP GIÁN TIẾP)

2.1     PHƯƠNG PHÁP 3: (Sử dụng tính chất 2.2 trang  2)

a) Phương pháp:

       Để tính khoảng cách từ điểm M đến mặt phẳng (P) ta làm như sau:

-        Tìm 1 đường thẳng a chứa M và song song với mặt phẳng (P). Khi đó:

     d(M, (P)) = d(a, (P)) = d(I, (P)), với mọi  I \[ \in \]a.

-        Chọn điểm I sao cho ta có thể tính khoảng cách từ I đến (P) một cách dễ dàng.

b) Các ví dụ:

Ví dụ 9: (Trích:  Đề thi tuyển sinh đại học D-2013)

Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, cạnh bên SA vuông góc với đáy, \[\widehat {BAD} = {120^0}\], M là trung điểm của BC và \[\widehat {SMA} = {45^0}\]. Tính khoảng cách từ điểm D đến mp(SBC).

Hướng dẫn:  Ở ví dụ này, việc xác định một mặt phẳng chứa D và vuông góc với (SBC) là khó khăn. Trong khi đó ta có thể dễ dàng thấy đường thẳng AD chứa D và song song với mp(SBC). Vậy ta chỉ cần chọn 1 điểm thuộc đường thẳng AD sao cho ta có thể xác định và tính được khoảng cách từ điểm đó đến (SBC).

Giải: 

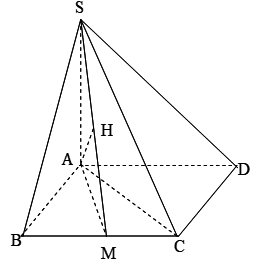
Vì AD//BC nên d(D,(SBC)) = d(A,(SBC)).

Sử dụng phương pháp 2 để xác định d(A,(SBC))

Ta có AM\[ \bot \]BC (vì \[\Delta \]ABC đều có AM là

trung tuyến đồng thời là đường cao)

          SA\[ \bot \]BC (vì SA\[ \bot \](ABCD))

\[ \Rightarrow \]BC\[ \bot \](SAM) \[ \Rightarrow \](SAM)\[ \bot \](SBC) = SM.

Kẻ AH \[ \bot \]SM tại H thì AH\[ \bot \](SBC)

\[ \Rightarrow \]AH = d(A, (SBC))

    AM = \[\frac{{a\sqrt 3 }}{2}\], \[\widehat {SMA} = {45^0}\]\[ \Rightarrow \]AH=AM.sin45⁰  = \[\frac{{a\sqrt 6 }}{4}\]

   Vậy d(D,(SBC)) = \[\frac{{a\sqrt 6 }}{4}\]

Ví dụ 10: (Trích: Đề thi tuyển sinh đại học khối B - 2013)

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ  điểm A đến mặt phẳng (SCD).

Hướng dẫn:  Ta thấy đường thẳng AB chứa A và song song với mp(SCD). Vậy ta chỉ cần chọn 1 điểm  H thuộc đường thẳng AB sao cho ta có thể xác định và tính được khoảng cách từ H đến (SCD).

Giải:  

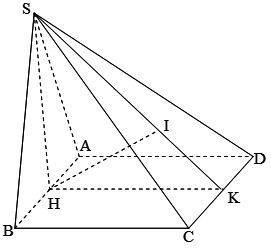
Gọi H, K lần lượt là trung điểm của AB và CD.

Ta có SH\[ \bot \]AB, (SAB) vuông góc với (ABCD)

theo giao tuyến AB nên SH \[ \bot \](ABCD)

Vì AB//CD nên AB//(SCD)

H \[ \in \]AB nên d(A,(SCD)) = d(H, (SCD))

Bằng cách sử dụng phương pháp 2 để xác định

d(H,(SBC)).

Ta có (SHK) chứa H và\[ \bot \](SCD)

(Vì  CD\[ \bot \]HK và \[ \bot \]SH nên CD \[ \bot \](SHK))

\[ \Rightarrow \] (SHK) \[ \bot \](SCD) = SK.

Gọi I là hình chiếu vuông góc của H trên SK thì HI\[ \bot \](SCD)\[ \Rightarrow \]HI = d(H,(SCD)).

Ta có SH = \[\frac{{a\sqrt 3 }}{2}\], HK = a

Trong tam giác SHK vuông tại H có HI là đường cao nên:

\[\frac{1}{{H{I^2}}} = \frac{1}{{H{S^2}}} + \frac{1}{{H{K^2}}}\] \[ \Leftrightarrow \]HI=\[\frac{{a\sqrt {21} }}{7}\]

Vậy d(A,(SCD)) = \[\frac{{a\sqrt {21} }}{7}\]