Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập trắc nghiệm khoảng cách có đáp án và lời giải, tài liệu bao gồm 82 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập trắc nghiệm khoảng cách có đáp án và lời giải

KHOẢNG CÁCH

A. CÂU HỎI

dạng 1. khoảng cách của hai điểm và các bài toán liên quan

Câu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là \[a\sqrt 2 \]và tam giác SAC đều. Tính độ dài cạnh bên của hình chóp.

A. 2a .

B. \[a\sqrt 2 \].

C. \[a\sqrt 3 \].

D. a .

Câu 2. Cho tứ diện ABCD có AC = 3a, BD = 4a. Gọi M, N lần lượt là trung điểm AD và BC. Biết AC vuông góc BD. Tính MN.

A. \[MN = \frac{{5a}}{2}.\]

B. \[MN = \frac{{7a}}{2}.\]

C. \[MN = \frac{{a\sqrt 7 }}{2}.\]

D. \[MN = \frac{{a\sqrt 5 }}{2}.\]

Câu 3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA ^ (ABC), góc giữa hai mặt phẳng (ABC) và (SBC) là 60⁰. Độ dài cạnh SA bằng

A. \[\frac{{3a}}{2}\].

B. \[\frac{a}{2}\].

C. \[a\sqrt 3 \].

D. \[\frac{a}{{\sqrt 3 }}\].

Câu 4. Cho hình lăng trụ ABC.A¢B¢C¢ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30⁰. Hình chiếu H của A trên mặt phẳng (A¢B¢C¢) là trung điểm của B¢C¢. Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.A¢B¢C¢.

A. \[\frac{a}{2}\].

B. \[\frac{a}{3}\].

C. \[\frac{{a\sqrt 3 }}{2}\].

D. \[\frac{{a\sqrt 2 }}{2}\].

Câu 5. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = 2a, CD = a, AA' = \[a\sqrt 2 \]. Đường chéo AC' có độ dài bằng

A. \[a\sqrt 5 \].

B. \[a\sqrt 7 \].

C. \[a\sqrt 6 \].

D. \[a\sqrt 3 \].

Câu 6. Cho hình hộp chữ nhật ABCD.A¢B¢C¢D¢ có AD = 2a, CD = a, AA¢ = \[a\sqrt 2 \]. Đường chéo AC¢ có độ dài bằng:

A. \[a\sqrt 5 \].

B. \[a\sqrt 7 \].

C. \[a\sqrt 6 \].

D. \[a\sqrt 3 \].

Câu 7. Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, BC = 3. Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng \[\frac{{\sqrt {11} }}{2}\]. Khi đó độ dài cạnh CD là

A. \[\sqrt 2 \].

B. 2 .

C. 1.

D. \[\sqrt 3 \].

Câu 8. Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt cùng phía so với (ABCD) song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (b) lần lượt cắt các nửa đường thẳng Ax, By, Cz, Dt tại A¢, B¢, C¢, D¢ thỏa mãn AA¢ = 2, BB¢ = 4, CC¢= 4. Hãy tính DD¢.

A. 3.

B. 7.

C. 2.

D. 5.

Câu 9. Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, BC = 3. Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng \[\frac{{\sqrt {11} }}{2}\]. Khi đó độ dài cạnh CD là

A. \[\sqrt 2 \].

B. 2 .

C. 1.

D. \[\sqrt 3 \].

Câu 10. Cho hình lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng \[4\sqrt 3 \]và cạnh bên bằng 12. Gọi M và N lần lượt là trung điểm của AA' và BC, gọi P và Q là hai điểm chạy trên đáy (A'B'C') sao cho PQ = 3. Giá trị nhỏ nhất của biểu thức T = MP + NQ bằng

A. \[8\sqrt 3 \].

B. \[3\sqrt {37} \].

C. \[3\sqrt {61} \].

D. \[6\sqrt {29} \].

Câu 11. Cho hình chóp S.ABCD có SA ^ (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.

A. \[\frac{{a\sqrt 2 }}{4}\].

B. \[\frac{{a\sqrt 3 }}{3}\].

C. \[\frac{{a\sqrt 3 }}{4}\].

D. \[\frac{{a\sqrt 2 }}{3}\].

Câu 12. Một hình lập phương được tạo thành khi xếp miếng bìa carton như hình vẽ bên. Tính khoảng cách từ điểm O đến đường thẳng AB sau khi xếp, biết rằng độ dài đoạn thẳng AB bằng 2a.

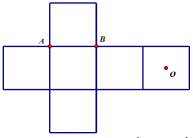
A. \[\frac{{a\sqrt 5 }}{2}.\]

B. \[\frac{{a\sqrt 5 }}{4}.\]

C. \[\frac{{a\sqrt 5 }}{3}.\]

D. \[a\sqrt 5 \]

Dạng 2. Khoảng cách từ 1 điểm đến 1 mặt phẳng

Dạng 2.1 Khoảng cách từ hình chiếu của đỉnh đến mặt phẳng bên

Câu 13. Cho hình chóp S. ABC có SA ^ (ABC), SA = AB = 2a, tam giác ABC vuông tại B (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng (SBC) bằng

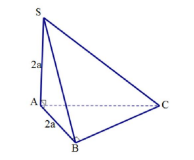
A . \[a\sqrt 3 \].

B. a .

C. 2a .

D. \[a\sqrt 2 \].

Câu 14. Cho hình chóp SABC có đáy là tam giác vuông tại A, AB = a, AC = \[a\sqrt 3 \], SA vuông góc với mặt phẳng đáy và SA = 2a. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng

A. \[\frac{{a\sqrt {57} }}{{19}}.\]

B. \[\frac{{2a\sqrt {57} }}{{19}}.\]

C. \[\frac{{2a\sqrt 3 }}{{19}}.\]

D. \[\frac{{2a\sqrt {38} }}{{19}}.\]

Câu 15. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, 2SA = AC = 2a và SA vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBC) là

A. \[\frac{{2a\sqrt 6 }}{3}.\]

B. \[\frac{{4a\sqrt 3 }}{3}.\]

C. \[\frac{{a\sqrt 6 }}{3}.\]

D. \[\frac{{a\sqrt 3 }}{3}.\]

Câu 16. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SB vuông góc với mặt phẳng đáy. Biết SB = 3a, AB = 4a, BC = 2a. Khoảng cách từ B đến mặt phẳng (SAC) bằng

A. \[\frac{{12\sqrt {61} a}}{{61}}.\]

B. \[\frac{{3\sqrt {14} a}}{{14}}.\]

C. \[\frac{{4a}}{5}.\]

D. \[\frac{{12\sqrt {29} a}}{{29}}.\]

Câu 17. Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a. Khoảng cách từ A đến mặt phẳng (SBC) bằng

A. \[\frac{{2\sqrt 5 a}}{5}.\]

B. \[\frac{{\sqrt 5 a}}{3}.\]

C. \[\frac{{2\sqrt 2 a}}{3}.\]

D. \[\frac{{\sqrt 5 a}}{5}.\]

Câu 18. Cho hình chóp S.ABCD có đáy là hình vuông cạnh\[\sqrt 3 a\], SA vuông góc với mặt phẳng đáy và SA = a. Khoảng cách từ A đến mặt phẳng (SBC) bằng

A. \[\frac{{\sqrt 5 a}}{3}.\]

B. \[\frac{{\sqrt 3 a}}{2}.\]

C. \[\frac{{\sqrt 6 a}}{6}.\]

D. \[\frac{{\sqrt 3 a}}{3}.\]

Câu 19. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, BC = a, SA vuông góc với mặt phẳng đáy và SA = a. Khoảng cách từ A đến mặt phẳng (SBC) bằng

A. \[\sqrt 2 a\].

B. \[\frac{{\sqrt 2 a}}{2}.\]

C. \[\frac{a}{2}.\]

D. \[\frac{{\sqrt 3 a}}{2}.\]

Câu 20. Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với mặt phẳng đáy và SA = a. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng

A. \[\frac{a}{2}.\]

B. a .

C. \[\frac{{a\sqrt 6 }}{3}.\]

D. \[\frac{{a\sqrt 2 }}{2}.\]

Câu 21. Cho hình lập phương ABCD.A¢B¢C¢D¢ có cạnh bằng 1. Tính khoảng cách d từ điểm A đến mặt phẳng (BDA¢).

A. \[d = \frac{{\sqrt 3 }}{3}.\]

B. \[d = \frac{{\sqrt 6 }}{4}.\]

C. \[d = \frac{{\sqrt 2 }}{2}.\]

D. \[d = \sqrt 3 .\]

Câu 22. Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A có BC = 2a, AB = \[a\sqrt 3 \], (tham khảo hình vẽ bên). Khoảng cách từ Ađến mặt phẳng (BCC'B') là

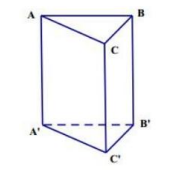
A. \[\frac{{a\sqrt 5 }}{2}.\]

B. \[\frac{{a\sqrt 7 }}{3}.\]

C. \[\frac{{a\sqrt 3 }}{2}.\]

D. \[\frac{{a\sqrt {21} }}{7}.\]

Câu 23. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Khoảng cách từ tâm O của đáy tới mp (SCD) bằng

A. \[\frac{a}{{\sqrt 2 }}.\]

B. \[\frac{a}{2}.\]

C. \[\frac{a}{{\sqrt 6 }}.\]

D. \[\frac{a}{{\sqrt 3 }}.\]

Câu 24. Cho hình chóp S.ABCD có đáy là hình vuông tâm O, SA vuông góc với mặt đáy. Hỏi mệnh đề nào sau đây là sai?

A. \[d\left( {B,(SCD} \right) = 2d\left( {O,(SCD)} \right)\].

B. \[d\left( {A,(SBD} \right) = d\left( {B,(SAC)} \right)\].

C. \[d\left( {C,(SAB} \right) = d\left( {C,(SAD)} \right)\].

D. \[d\left( {S,(ABCD} \right) = SA.\]

Câu 25. Cho hình chóp S.ABC có tam giác ABC là tam giác vuông tại A, AC = \[a\sqrt 3 \], \[\widehat {ABC} = {30^0}\]. Góc giữa SC và mặt phẳng ABC bằng 60⁰. Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến (SBC) bằng bao nhiêu?

A. \[\frac{{a\sqrt 6 }}{{\sqrt {35} }}.\]

B. \[\frac{{a\sqrt 3 }}{{\sqrt {35} }}.\]

C. \[\frac{{2a\sqrt 3 }}{{\sqrt {35} }}.\]

D. \[\frac{{3a}}{{\sqrt 5 }}.\]

Câu 26. Cho hình chóp S.MNPQ có đáy là hình vuông cạnh MN = \[3a\sqrt 2 \], SM vuông góc với mặt phẳng đáy, SM = 3a, với 0 < a Î R. Khoảng cách từ điểm M đến mặt phẳng (SNP) bằng

A. \[a\sqrt 3 \].

B. \[2a\sqrt 6 \].

C. \[2a\sqrt 3 \].

D. \[a\sqrt 6 \].

Câu 27. Cho hình chóp S.ABCD có đường cao SA = 2a, đáy ABCD là hình thang vuông ở A và D, AB = 2a, AD = CD = a. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng

A. \[\frac{{2a}}{{\sqrt 3 }}.\]

B. \[\frac{{2a}}{{\sqrt 2 }}.\]

C. \[\frac{{2a}}{{\sqrt 3 }}.\]

D. \[a\sqrt 2 \].

Câu 28. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông cân tại B, AC = \[a\sqrt 2 \]. Gọi G là trọng tâm tam giác SAB và K là hình chiếu của điểm A trên cạnh SC. Gọi a là góc giữa hai mặt phẳng (ABC) và (AGK). Tính cosa , biết rằng khoảng cách từ điểm A đến mặt phẳng (KBC) bằng \[\frac{a}{{\sqrt 2 }}\].

A. \[\cos \alpha  = \frac{1}{2}.\]

B. \[\cos \alpha  = \frac{{\sqrt 2 }}{2}.\]

C. \[\cos \alpha  = \frac{{\sqrt 3 }}{2}.\]

D. \[\cos \alpha  = \frac{{\sqrt 3 }}{3}.\]

Câu 29. Cho hình chóp S ABC có SA = 3a và SA ^ (ABC). Biết AB = BC = 2a, \[\widehat {ABC} = {120^0}\]. Khoảng cách từ A đến (SBC) bằng

A. \[\frac{{3a}}{2}.\]

B. \[\frac{a}{2}.\]

C. a.

D. 2a.

Câu 30. Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính khoảng cách từ A đến mặt phẳng (A'BD) theo a .

A. \[\frac{{a\sqrt 3 }}{3}.\]

B. \[a\sqrt 3 \].

C. \[2a\sqrt 3 \].

D. \[\frac{{a\sqrt 3 }}{6}.\]

Câu 31. Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng

A. \[\frac{{a\sqrt {12} }}{7}\].

B. \[\frac{{a\sqrt {21} }}{7}.\]

C. \[\frac{{a\sqrt 6 }}{4}.\]

D. \[\frac{{a\sqrt 3 }}{4}.\]