Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tóm tắt lý thuyết và bài tập trắc nghiệm hàm số mũ và hàm số logarit, tài liệu bao gồm 13 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt lý thuyết và bài tập trắc nghiệm hàm số mũ và hàm số logarit

A. LÝ THUYẾT VỀ HẦM SỐ LOGARIT VÀ HÀM SỐ MŨ

I. Hàm số logarit

1. Định nghĩa

Cho a là số thực dương và a¹1. Hàm số \[y = {\log _a}x\] được gọi là hàm số logaritt cơ số a .

2. Đạo hàm hàm số lôgarit

\[\begin{array}{l}y = {\log _a}x \Rightarrow y' = \frac{1}{{x\ln a}};\\y = \ln x \Rightarrow y' = \frac{1}{x};\\y = {\log _a}u(x) \Rightarrow y' = \frac{{u'}}{{u\ln a}}.\end{array}\]

3. Khảo sát hàm số lôgarit

Tập xác định. Tập xác định của hàm số logarit \[y = {\log _a}x\] ( a > 0; a ¹ 1) là (0;+∞).

Chiều biến thiên. a >1: Hàm số đồng biến.

                             0 < a < 1 : Hàm số nghịch biến.

Tiệm cận. Trục tung Oy là đường tiệm cận đứng

Đồ thị. Đồ thị đi qua điểm M (1;0), N ( a;1) và nằm phía bên phải trục tung.

II. Hàm số mũ:

1. Định nghĩa

Cho a là số thực dương và a ¹1. Hàm số  y = a^x được gọi là hàm số mũ cơ số a.

2. Đạo hàm của hàm số mũ

\[\begin{array}{l}y = {e^x} \Rightarrow y' = {e^x};\\y = {a^x} \Rightarrow y' = {a^x}\ln a;\\y = {a^{u(x)}} \Rightarrow y' = {a^u}\ln au'.\end{array}\]

3. Khảo sát hàm số mũ

Tập xác định. Tập xác định của hàm số mũ y = a^x ( a > 0; a ¹ 1) là \[\mathbb{R}\] .

Chiều biến thiên. a > 1: Hàm số luôn đồng biến.

                            0 < a < 1 : Hàm số luôn nghịch biến.

Tiệm cận. Trục hoành Ox là đường tiệm cận ngang.

Đồ thị. Đồ thị đi qua điểm (1;0), (1;a) và nằm phía trên trục hoành.

Nhận xét. Đồ thị hàm số y = a^x và đồ thị hàm số \[y = {\log _a}x\] đối xứng với nhau qua đường thẳng y = x .

B. BÀI TẬP VỀ HÀM SỐ LOGARIT VÀ HÀM SỐ MŨ

Phần 1: Nhận biết – Thông hiểu

Câu 1. Tìm mệnh đề đúng trong các mệnh đề sau:

A. Đồ thị hàm số y = a^x và đồ thị hàm số và đồ thị hàm số \[y = {\log _a}x\] đối xứng với nhau qua đường thẳng y = x .

B. Đồ thị hàm số y = a^x với 0 < a < 1 đồng biến trên khoảng (−∞ +∞) .

C. Đồ thị hàm số y = a^x với a > 1 nghịch biến trên khoảng (−∞ +∞) .

D. Hàm số y = a^x với a > 0 và a ¹ 1 luôn đi qua điểm M (a ;1) .

Câu 2. Tập giá trị của hàm số y = a^x ( a > 0; a ¹ 1) là

A. (0;+ ∞)

B. [0;+ ∞)

C. \[\mathbb{R}\]\{0}

D. \[\mathbb{R}\]

Câu 3. Với a > 0 và a ≠ 1. Phát biểu nào sau đây không đúng?

A. Hai hàm số y = a^x và \[y = {\log _a}x\] có cùng tập giá trị.

B. Hai hàm số y = a^x và \[y = {\log _a}x\] có cùng g tính đơn điệu.

C. Đồ thị hai hàm số y = a^x và \[y = {\log _a}x\] đối xứng nhau qua đường thẳng y x = .

D. Đồ thị hai hàm số y = a^x và \[y = {\log _a}x\] đều có đường tiệm cận.

Câu 4. Cho hàm số \[y = {(\sqrt 2  - 1)^x}\]. Phát biểu nào sau đây là đúng?

A. Hàm số nghịch biến trên khoảng (−∞; +∞) .

B. Hàm số đồng biến trên khoảng (0; +∞) .

C. Đồ thị hàm số có đường tiệm cận ngang là trục tung.

D. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.

Câu 5. Tập xác định của hàm số \[y = {(2x - 1)^{2017}}\] là:

A. \[D = \mathbb{R}\]

B. \[D = \left( {\frac{1}{2}; + \infty } \right)\]

C. \[D = \left[ {\frac{1}{2}; + \infty } \right]\]

D. \[D = \mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\]

Câu 6. Tập xác định của hàm số y = (3x² – 1)^-2 là:

A. \[D = \mathbb{R}\backslash \left\{ { \pm \frac{1}{{\sqrt 3 }}} \right\}\]

B. \[D = \left\{ { \pm \frac{1}{{\sqrt 3 }}} \right\}\]

C. \[D = \left( { - \infty ; - \frac{1}{{\sqrt 3 }}} \right) \cup \left( {\frac{1}{{\sqrt 3 }}; + \infty } \right)\]

D. \[D = \left( { - \frac{1}{{\sqrt 3 }};\frac{1}{{\sqrt 3 }}} \right)\]

Câu 7. Tập xác định của hàm số y = (x² – 3x+2)^-e là:

A. \[D = \left( { - \infty ;1} \right) \cup \left( {2; + \infty } \right)\]

B. \[D = \mathbb{R}\backslash \left\{ {1;2} \right\}\]

C. \[D = \left( {0; + \infty } \right)\]

D. \[D = \left( {1;2} \right)\]

Câu 8. Tập xác định của hàm số \[y = {\log _{0,5}}(x + 1)\] là:

A. \[D = \left( { - 1; + \infty } \right)\]

B. \[D = \mathbb{R}\backslash \left\{ 1 \right\}\]

C. \[D = \left( {0; + \infty } \right)\]

D. \[D = \left( { - \infty ; - 1} \right)\]

Câu 9. Tìm x để hàm số \[y = \log \sqrt {{x^2} + x - 12} \]có nghĩa.

A. \[x \in \left( { - \infty ; - 4} \right) \cup (3; + \infty )\]

B. \[x \in  \cup ( - 4;3)\]

C. \[\left\{ {\begin{array}{*{20}{c}}{x \ne  - 4}\\{x \ne 3}\end{array}} \right.\]

D. \[x \in \mathbb{R}\]

Câu 10. Tập xác định của hàm số \[y = {\log _x}\frac{{x + 3}}{{2 - x}}\] là:

A. \[D = ( - 3;2)\]

B. \[D = \mathbb{R}\backslash ( - 3;2)\]

C. \[D = ( - \infty ; - 3) \cup \left( {2; + \infty } \right)\]

D. \[D = \left[ { - 3;2} \right]\]

Câu 11. Tập xác định của hàm số \[y = \frac{1}{{\sqrt {2 - x} }} + \ln (x - 1)\] là:

A. D = (1; 2)

B. D = (1; +∞)

C. D = (0; +∞)

D. D = [1; 2]

Câu 12. Tập xác định của hàm số \[y = \frac{{{e^x}}}{{{e^x} - 1}}\] là:

A. \[D = \mathbb{R}\backslash \left\{ 0 \right\}\]

B. D = (0; +∞)

C.  \[D = \mathbb{R}\backslash 1\]

D. D = (e; +∞)

Câu 13. Tập xác định \[y = \sqrt { - 2{x^2} + 5x - 2}  + \ln \frac{1}{{{x^2} - 1}}\] là:

A. D = (1;2]

B. D = [1;2]

C. D = (-1;1)

D. D = (-1;2)

Câu 14. Tập xác định của hàm số y = ln(ln x) là :

A. D = (1; +∞)

B. D = (0; +∞)

C. D = (e; +∞)

D. D = [1; +∞)

Câu 15. Tập xác định của hàm số y = (3^x – 9)^-2 là:

A. \[D = \mathbb{R}\backslash \left\{ 2 \right\}\]

B. \[D = \mathbb{R}\backslash \left\{ 0 \right\}\]

C. D = (2; +∞)

D. D = (0; +∞)

Câu 16. Hàm số \[y = {\log _{x - 1}}x\] xác định khi và chỉ khi :

A. \[\left\{ {\begin{array}{*{20}{c}}{x > 1}\\{x \ne 2}\end{array}} \right.\]

B. x > 1

C. x > 0

D. x ≠ 2

Câu 17. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

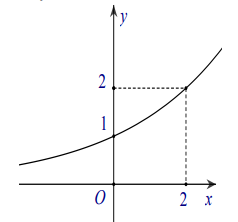
A. \[y = {\left( {\sqrt 2 } \right)^x}\]

B. y = x

C. y = 2^x

D. \[y = {\left( {\sqrt 2 } \right)^{ - x}}\]

Câu 18. Hàm số \[y = {\left( {x - 1} \right)^{\frac{1}{3}}}\] có đạo hàm là:

A. \[y' = \frac{1}{{3\sqrt[3]{{{{(x - 1)}^2}}}}}\]

B. \[y' = \frac{1}{{3\sqrt {{{(x - 1)}^3}} }}\]

C. \[y' = \frac{{\sqrt[3]{{{{(x - 1)}^2}}}}}{3}\]

D. \[y' = \frac{{\sqrt {{{(x - 1)}^3}} }}{3}\]

Câu 19. Đạo hàm của hàm số y = 4^2x  là:

A. \[y' = {2.4^{2x}}\ln 4\]

B. \[y' = {4^{2x}}.\ln 2\]

C. \[y' = {4^{2x}}.\ln 4\]

D. \[y' = {2.4^{2x}}.\ln 2\]

Câu 20. Đạo hàm của hàm số \[y = {\log _5}x,x > 0\] là

A. \[y' = \frac{1}{{x\ln 5}}\]

B. \[y' = x\ln 5\]

C. \[y' = {5^x}\ln 5\]

D. \[y' = \frac{1}{{{5^x}\ln 5}}\]

Câu 21. Hàm số \[y = {\log _{0,5}}{x^2}(x \ne 0)\]có công thức đạo hàm là:

A. \[y' = \frac{1}{{x\ln 0,5}}\]

B. \[y' = \frac{1}{{{x^2}\ln 0,5}}\]

C. \[y' = \frac{2}{{{x^2}\ln 0,5}}\]

D. \[y' = \frac{1}{{x\ln 0,5}}\]

Câu 22. Đạo hàm của hàm số \[y = \sin x + {\log _3}{x^3}(x > 0)\] là:

A. \[y' = \cos x + \frac{3}{{x\ln 3}}\]

B. \[y' =  - \cos x + \frac{3}{{x\ln 3}}\]

C. \[y' = \cos x + \frac{3}{{{x^3}\ln 3}}\]

D. \[y' =  - \cos x + \frac{3}{{{x^3}\ln 3}}\]

Câu 23. Cho hàm số f(x) = ln( x⁴ + 1). Đạo hàm \[f'(0)\] bằng:

A. 0

B. 1

C. 2

D. 3

Câu 24. Cho hàm số \[f(x) = {e^{2017{x^2}}}\]. Đạo hàm \[f'(0)\] bằng:

A. 0

B. 1

C. e

D. e²⁰¹⁷

Câu 25. Cho hàm số f(x) = xe^x . Gọi \[f''(x)\]là đạo hàm cấp hai của f(x). Ta có \[f''(1)\] bằng:

A. 3e

B. -3e²

C. e³

D. -5e²

Câu 26. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

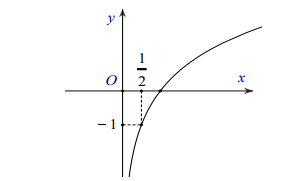
A. \[y = {\log _2}x\]

B. \[y = {\log _{\frac{1}{2}}}x\]

C. \[y = {\log _{\sqrt 2 }}x\]

D. \[y = {\log _2}(2x)\]

Câu 27. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. Hàm số y = a^x có tập xác định là D = \[\mathbb{R}\].

B. Đồ thị hàm số y = a^x  với α > 0 không có tiệm cận.

C. Hàm số y = a^x với α < 0 nghịch biến trên khoảng (0; +∞).

D. Đồ thị hàm số y = a^x  với α < 0 có hai tiệm cận.

Câu 28. Trong các mệnh đề sau mệnh đề nào đúng?

A. Đồ thị hàm số lôgarit nằm bên phải trục tung.

B. Đồ thị hàm số lôgarit nằm bên trái trục tung.

C. Đồ thị hàm số mũ nằm bên phải trục tung.

D. Đồ thị hàm số mũ nằm bên trái trục tung.

Câu 29. Chọn phát biểu sai trong các phát biểu sau?

A. Đồ thị hàm số logarit nằm bên trên trục hoành.

B. Đồ thị hàm số mũ không nằm bên dưới trục hoành.

C. Đồ thị hàm số lôgarit nằm bên phải trục tung.

D. Đồ thị hàm số mũ với số mũ âm luôn có hai tiệm cận.

Câu 30. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

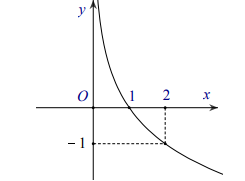
A. \[y = {\log _{0,5}}x\]

B. \[y = {\log _2}x\]

C. \[y =  - \frac{1}{3}x - \frac{1}{3}\]

D. \[y =  - 3x + 1\]

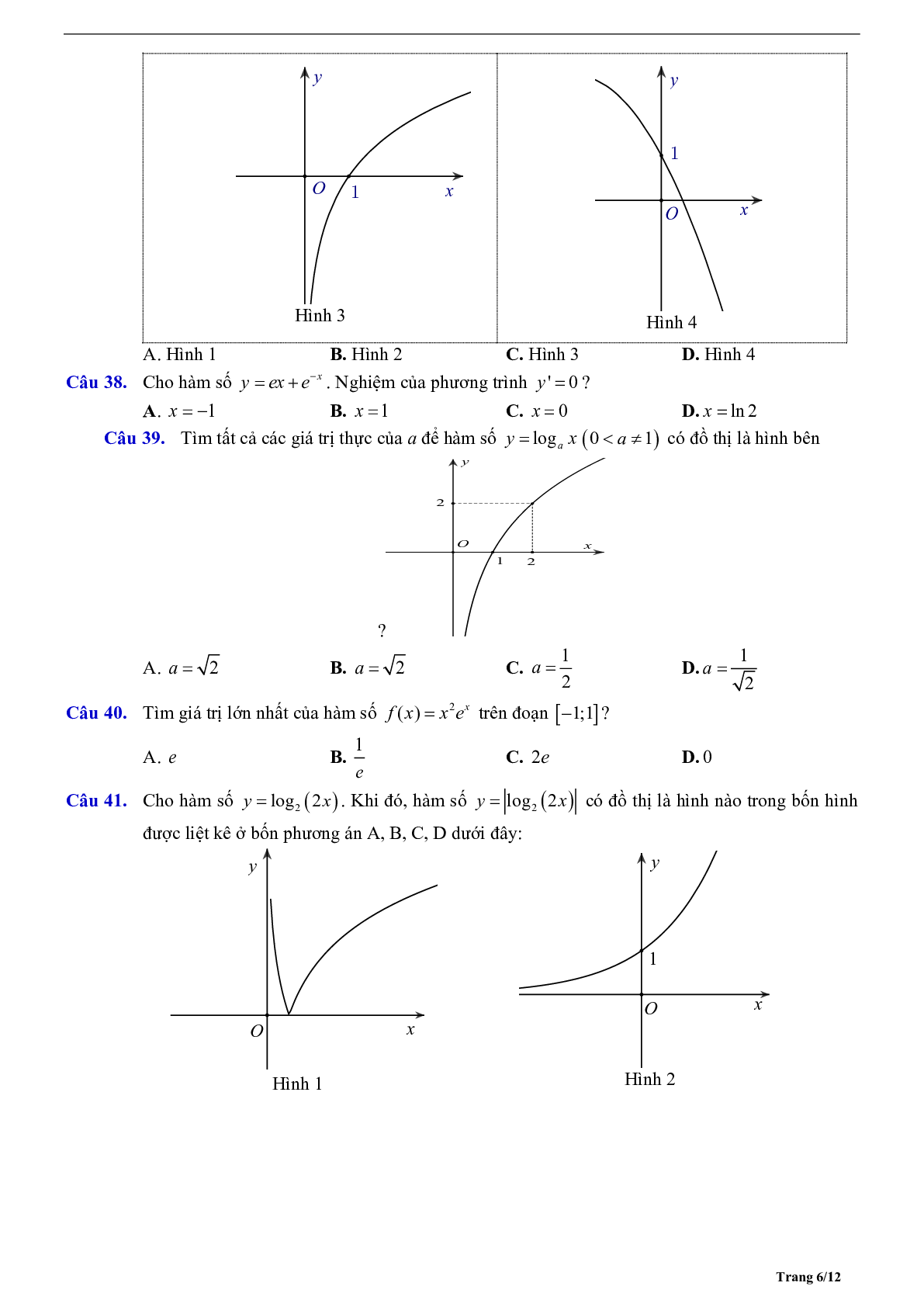
Câu 31. Tìm a để hàm số \[y = {\log _a}x(0 < a \ne 1)\] có đồ thị là hình bên dưới:

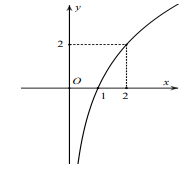
A. \[a = \sqrt 2 \]

B. a = 2

C. a = \[\frac{1}{2}\]

D. a = \[\frac{1}{{\sqrt 2 }}\]

Phần 2: Vận dụng thấp

Câu 32. Tìm tập xác định D của hàm số \[y = {\log _3}\frac{{10 - x}}{{{x^2} - 3x + 2}}\].

A. \[D = ( - \infty ;1) \cup \left( {2;10} \right)\]

B. \[D = (1; + \infty )\]

C. \[D = ( - \infty ;10)\]

D. D = (2;10)

Câu 33. Tìm tập xác định D của hàm số \[y = \sqrt {{{\log }_3}(x - 2) - 3} \]?

A. D = [29; +∞ )

B. D = (29;+∞)

C. D = (2;29)

D. D =  (2; +∞)

Câu 34. Tính đạo hàm của hàm số y = (x²+2x)e^-x ?

A. \[y' = ( - {x^2} + 2){e^{ - x}}\]

B. \[y' = ({x^2} + 2){e^{ - x}}\]

C. \[y' = x{e^{ - x}}\]

D. \[y' = (2x - 2){e^x}\]

Câu 35. Tìm tất cả các giá trị thực của tham số m để hàm số y = ln (x² -2mx+4) có tập xác định D = \[\mathbb{R}\]?

A. -2 < m < 2

B. \[\left[ {\begin{array}{*{20}{c}}{m > 2}\\{m <  - 2}\end{array}} \right.\]

C. m > -2

D. \[ - 2 \le m \le 2\]

Câu 36. Cho tập D = (3;4) và các hàm số \[f(x) = \frac{{2017}}{{\sqrt {{x^2} - 7x + 12} }};g(x) = {\log _{x - 3}}(4 - x);h(x) = {3^{{x^2} - 7x + 12}}\].D là tập xác định của hàm số nào?

A. f(x) và f(x) +g(x)

B. f(x) và h(x)

C. g(x) và h(x)

D. f(x) + h(x) và h(x)