Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Phương trình, bất phương trình mũ và logarit Toán lớp 12, tài liệu bao gồm 96 trang, tuyển chọn 126 bài tập Phương trình, bất phương trình mũ và logarit đầy đủ lý thuyết, phương pháp giải chi tiết và lời giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
- Tóm tắt ngắn gọn kiến thức trọng tâm cần nhớ và một số bài tập cho từng dạng bài
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
A. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH – BPT MŨ - LOGARIT
1. Phương trình mũ
a. Phương trình mũ cơ bản.
Phương trình mũ cơ bản có dạng: ax = m (1).
Nếu m > 0 thì phương trình (1) có nghiệm duy nhất x = logam.
Nếu m ≤ 0 thì phương trình (1) vô nghiệm.
b. Phương pháp đưa về cùng cơ số.
Với a > 0 và a ≠ 1 ta có af(x) = ag(x) ⇔ f(x) = g(x).
c. Phương pháp lôgarit hoá.
af(x) = b ⇔ f(x) = logab
af(x) = bg(x) ⇔ f(x) = g(x)logab
logaf(x) = b ⇔ f(x) = ab
d. Phương pháp đặt ẩn phụ
Dạng 1: Phương trình αk + αk-1 a(k-1)x + ... + α1 ax + α0 = 0
Khi đó ta đặt t = ax điều kiện t > 0, ta được αk tk + αk-1 tk-1 + ... + α1 t + α0 = 0
Mở rộng: Nếu đặt t = af(x) , điều kiện hẹp t > 0.
Dạng 2: Phương trình α1 ax + α2 ax + α3 = 0 với a.b = 1
Mở rộng: Với a.b = 1 thì khi đặt t = af(x), điều kiện hẹp t > 0, suy ra
Dạng 3: Phương trình α1 a2x + α2 (a.b)x + α3 b2x = 0 khi đó chia hai vế của phương trình cho b2x > 0 (hoặc a2x, (a.b)x), điều kiện t < 0, ta được
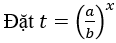
Mở rộng: Với phương trình mũ có chứa các nhân tử: a2f, b2f, (a.b)2f, ta thực hiện theo các bước sau:
+ Chia 2 vế của phương trình cho b2f > 0 (hoặc a2f,(a.b)f)
+ Đặt 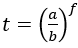
e. Phương pháp sử dụng tính đơn điệu
Hướng 1:
• Bước 1. Chuyển phương trình về dạng f(x)=k.
• Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D. Khẳng định hàm số đơn điệu
• Bước 3. Nhận xét:
+ Với x = x0 ⇔ f(x) = f(x0) = k do đó x = x0 là nghiệm.
+ Với x > x0 ⇔ f(x) > f(x0) = k do đó phương trình vô nghiệm.
+ Với x < x0 ⇔ f(x) < f(x0) = k do đó phương trình vô nghiệm.
• Bước 4. Kết luận vậy x = x0 là nghiệm duy nhất của phương trình.
Hướng 2:
• Bước 1. Chuyển phương trình về dạng f(x) = g(x).
• Bước 2. Khảo sát sự biến thiên của hàm số y = f(x) và y = g(x). Khẳng định hàm số y = f(x) là hàm số đồng biến còn y = g(x) là hàm số nghịch biến hoặc là hàm hằng.
• Bước 3. Xác đinh x0 sao cho f(x0) = g(x0 .
• Bước 4. Kết luận vậy x = x0 là nghiệm duy nhất của phương trình.
Hướng 3:
• Bước 1. Chuyển phương trình về dạng f(u) = f(v).
• Bước 2. Khảo sát sự biến thiên của hàm số y = f(x). Khẳng định hàm số đơn điệu.
• Bước 3. Khi đó f(u) = f(v) ⇔ u = v.
2. Bất phương trình mũ
Bất phương trình mũ cơ bản có dạng ax > b (hoặc ax ≥ b, ax < b, ax ≤ b) với a > 0, a ≠ 1.
Ta xét bất phương trình có dạng ax > b.
• Nếu b ≤ 0, tập nghiệm của bất phương trình là R, vì ax > b, ∀x ∈ R..
• Nếu b > 0 thì bất phương trình tương đương với ax > alogab.
Với a > 1, nghiệm của bất phương trình là x > loga b.
Với 0 < a < 1, nghiệm của bất phương trình là x < loga b.
Ta minh họa bằng đồ thị sau:
• Với a > 1, ta có đồ thị sau.
• Với 0 < a < 1, ta có đồ thị sau.
Lưu ý:
1. Dạng 1:
2. Dạng 2:
3. Dạng 3: af(x) > b(*)
4. Dạng 4: af(x) < b(**)
Lưu ý: Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.
Tương tự với bất phương trình dạng:
Trong trường hợp cơ số a có chứa ẩn số thì:
Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
+ Đưa về cùng cơ số.
+ Đặt ẩn phụ.
+ Sử dụng tính đơn điệu:
3. Phương trình logarit
a. Định nghĩa
Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
b. Phương trình lôgarit cơ bản
• loga x = b ⇔ x = ab (0 < a ≠ 1).
• loga f(x) = loga g(x)
c. Phương pháp đưa về cùng cơ số
* Bước 1. Tìm điều kiện của phương trình (nếu có).
* Bước 2. Sử dụng định nghĩa và các tính chất của lôgarit để đưa các lôgarit có mặt trong phương trình về cùng cơ số.
* Bước 3.Biến đổi phương trình về phương trình lôgarit cơ bản đã biết cách giải.
* Bước 4. Kiểm tra điều kiện và kết luận.
d. Phương pháp mũ hóa
loga f(x) = g(x) (0 < a ≠ 1) ⇔ f(x) = ag(x)
e. Phương pháp đặt ẩn phụ
Giải phương trình: f[logag(x)] = 0 (0 < a ≠ 1).
• Bước 1: Đặt t = logag(x) (*).
• Bước 2: Tìm điều kiện củat (nếu có).
• Bước 3: Đưa về giải phương trình f(t) = 0 đã biết cách giải.
•Bước 4: Thay vào (*) để tìm x.
f. Một số lưu ý quan trọng khi biến đổi
1) logaf2(x) = 2loga|f(x)|
2) logaf2k(x) = 2kloga|f(x)|
3) logaf2k+1(x) = (2k+1)logaf(x)
4) loga(f(x)g(x)) = loga|f(x)| + loga|g(x)|
4. Bất phương trình logarit
a. Phương trình logarit đơn giản
| logax ≤ b | Nghiệm |
| 0 < a < 1 | x ≥ ab |
| a > 1 | 0 < x ≤ ab |
| logax ≥ b | Nghiệm |
| 0 < a < 1 | 0 < x ≤ ab |
| a > 1 | x ≥ ab |
b. Phương pháp đưa về cùng cơ số
| logaf(x) ≤ logag(x) | |
| 0 < a < 1 | logaf(x) ≤ logag(x) ⇔ f(x) ≥ g(x) > 0 |
| a > 1 | logaf(x) ≤ logag(x) ⇔ 0 < f(x) ≤ g(x) |
| logaf(x) ≥ logag(x) | |
| 0 < a < 1 | logaf(x) ≥ logag(x) ⇔ 0 < f(x) ≤ g(x) |
| a > 1 | logaf(x) ≥ logag(x) ⇔ f(x) ≥ g(x) > 0 |
c. Phương pháp đặt ẩn phụ
Mục đích chính của phương pháp này là chuyển các bài toán đã cho về bất phương trình đại số quen thuộc, đặc biệt là các bất phương trình bậc hai hoặc hệ bất phương trình.
B. BÀI TẬP
Bài 1: Giải phương trình sau
Hướng dẫn:
Bài 2: Giải phương trình sau: (7+4√3)x-3(2-√3)x+2=0
Hướng dẫn:
Nhận xét rằng 7+4√3=(2+√3)2; (2+√3)(2-√3)=1
Do đó nếu đặt t=(2+√3)x điều kiện t > 0 thì (2-√3)x=1/t và (7+4√3)x = t2
Khi đó phương trình đã cho tương đương với
Vậy phương trình có nghiệm x=0
Bài 3: Giải phương trình 2x2-x + 93-2x + x2 + 6 = 42x-3 + 3x - x2 + 5x (*).
Hướng dẫn:
Ta có: (*) ⇔ 2x2-x + 36-4x + x2 + 6 = 24x-6 + 3x-x2 + 5x.
⇔ 2x2-x + x2 - x - 3x-x2 = 24x-6 + 4x - 6 - 36-4x.
ta được 2u + u - 3-u = 2v + v - 3-v.
Xét hàm số:
⇒ f'(t) là hàm số đồng biến trên R, mà f(u)=f(v) ⇔ u=v.
Ta có phương trình:
Vậy tập nghiệm của phương trình là: S={1;6}.
Bài 4: Giải bất phương trình sau 9x-1-36.3x-3+3 ≤ 0
Hướng dẫn:
Biến đổi bất phương trình (1) ta được
(1) ⇔ (3x-1)2-4.3x-1+3 ≤ 0 (2)
Đặt t = 3x-1 (t > 0), bất phương trình (2) trở thành t2-4t+3 ≤ 0 (3)
(3) ⇔ 1 ≤ t ≤ 3
Suy ra: 1 ≤ 3x-1 ≤ 3 ⇔ 0 ≤ x-1 ≤ 1 ⇔ 1 ≤ x ≤ 2
Vậy tập nghiệm của bất phương trình là S = [1;2]
Bài 5: Tập nghiệm của bất phương trình 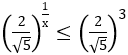
Hướng dẫn:
Vì 2/√5 < 1 nên bất phương trình tương đương với
Vậy tập nghiệm của bất phương trình là (0;1/3]
Bài 6: Tập nghiệm của bất phương trình 3x.2x+1 ≥ 72 là:
A. x ∈ [2; +∞). B. x ∈ (-∞; 2].
C. x ∈ (-∞; 2). D. x ∈ (2; +∞).
Hướng dẫn :
Ta có 3x.2x+1 ≥ 72 ⇔ 2.6x ≥ 72 ⇔ x ≥ 2
Bài 7: Giải phương trình log23 x - 4log3x + 3 = 0.
Hướng dẫn:
Điều kiện của phương trình là x > 0.
Đặt log3x = t. Khi đó phương trình đã cho trở thành
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {3;27}.
Bài 8: Giải phương trình log(25x - 22x+1) = x.
Hướng dẫn:
log(25x-22x+1 )=x ⇔ 25x-22x+1=10x ⇔ 25x-2.4x=10x
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là
Bài 9: Giải bất phương trình sau
Hướng dẫn:
Bài 10: Giải bất phương trình sau
Hướng dẫn:
Đặt t=log2x ≠ 0. Khi đó bất phương trình trở thành.
Vậy tập nghiệm của bất phương trình là:









