Bài tập về Đồ thị hàm lũy thừa, hàm số mũ, hàm số logarit chọn lọc

Quý Lê Xuân Ngày: 08-03-2024 Lớp 12

Tải xuống 6 5.8 K 88

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Đồ thị hàm lũy thừa, hàm sô mũ, hàm số logarit Toán lớp 12, tài liệu bao gồm 6 trang có phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Bài tập Đồ thị hàm lũy thừa, hàm sô mũ, hàm số logarit gồm các nội dung chính sau:

A. Phương phương giải

- Tóm tắt lý thuyết ngắn gọn và phương pháp giải Đồ thị hàm lũy thừa, hàm sô mũ, hàm số logarit.

B. Bài tập

- Gồm 12 bài tập tự luyện có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Đồ thị hàm lũy thừa, hàm sô mũ, hàm số logarit.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Bài tập Đồ thị hàm lũy thừa, hàm sô mũ, hàm số logarit (ảnh 1)

ĐỒ THỊ HÀM LŨY THỪA, MŨ, LOGARIT

A. PHƯƠNG PHÁP GIẢI

+) Hàm số lũy thừa

Tính chất của hàm số lũy thừa trên khoảng $(0; + \infty)$

· $y = x^{α} > 0$ $(\forall x \in (0; + \infty))$

· Đồ thị hàm số luôn đi qua điểm $(1; 1)$

· Khi $α > 0 \Rightarrow y' = (x^{α})' = α . x^{α - 1} > 0$ $(\forall x \in (0; + \infty))$ hàm số luôn đồng biến

Trong trường hợp này $\lim_{x \to + \infty} x^{α} = + \infty; \lim_{x \to 0^{+}} x^{α} = 0$ do đó đồ thị hàm số không có đường tiệm cận

· Khi $α < 0 \Rightarrow y' = (x^{α})' = α . x^{α - 1} < 0$ $(\forall x \in (0; + \infty))$ hàm số luôn nghịch biến

Trong trường hợp này $\lim_{x \to + \infty} x^{α} = 0; \lim_{x \to 0^{+}} x^{α} = + \infty$ do đó đồ thị hàm số nhận trục $O x$ là đường tiệm cận ngang và trục $O y$ là đường tiệm cận đứng.

Đồ thị hàm số lũy thừa $y = x^{a}$ trên khoảng $(0; + \infty)$

Đồ thị hàm số $y = x^{α}$ luôn đi qua điểm $I (1; 1) .$

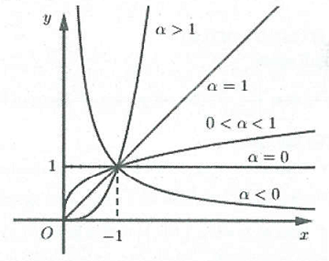
Bài tập Đồ thị hàm lũy thừa, hàm sô mũ, hàm số logarit (ảnh 2)

Lưu ý: Khi khảo sát hàm số lũy thừa với sỗ mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn:

Hàm số: $y = x^{3}$ $(x \in ℝ) .$

Hàm số: $y = x^{- 4}$ $(x \neq 0) .$

Hàm số: $y = x^{\frac{1}{3}}$ $(x > 0) .$

+) Hàm số mũ

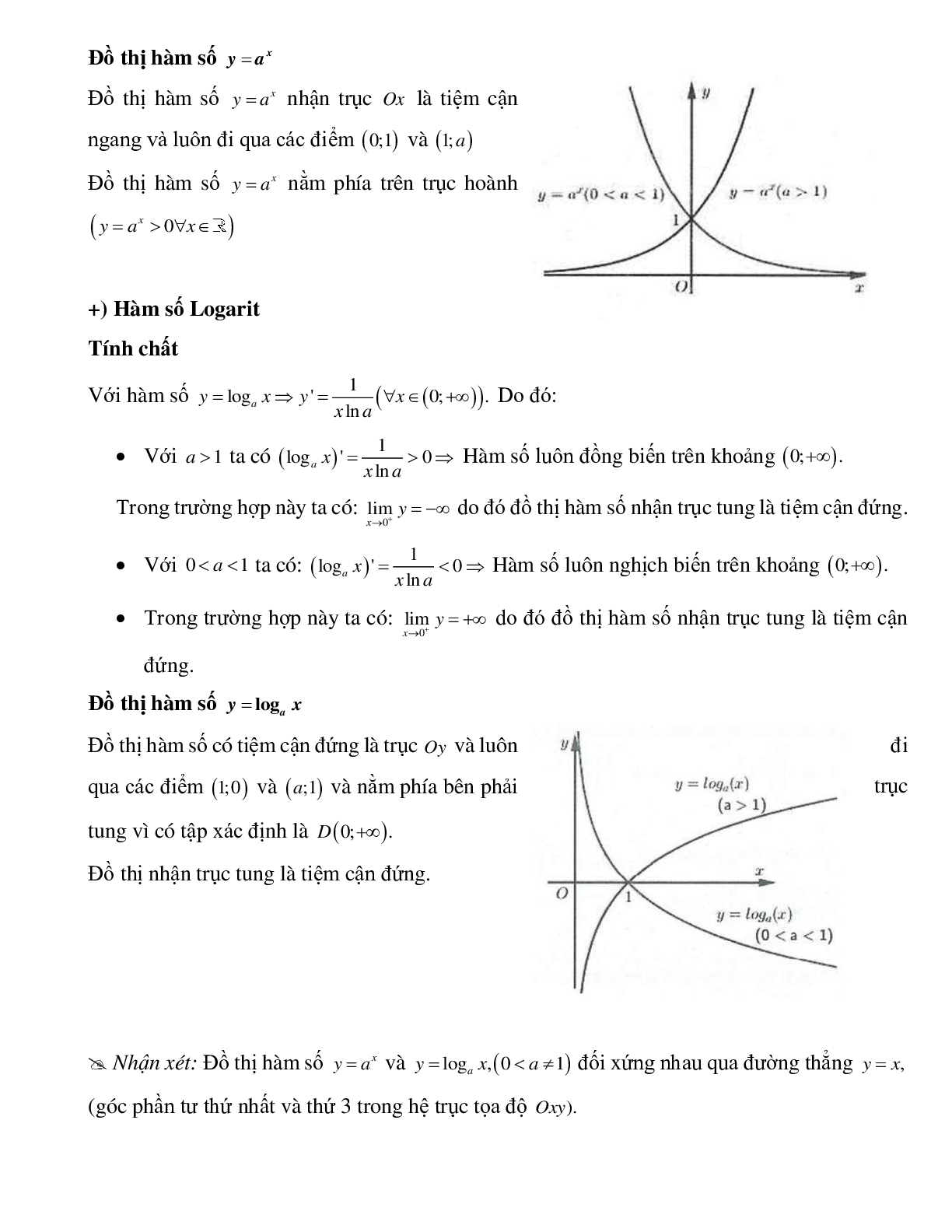
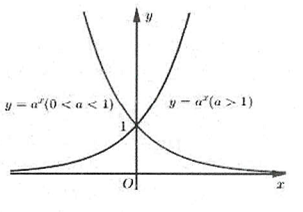
Đồ thị hàm số $y = a^{x}$

Đồ thị hàm số $y = a^{x}$ nhận trục $O x$ là tiệm cận ngang và luôn đi qua các điểm $(0; 1)$ và $(1; a)$

Đồ thị hàm số $y = a^{x}$ nằm phía trên trục hoành $(y = a^{x} > 0 \forall x \in ℝ)$

+) Hàm số Logarit

Tính chất

Với hàm số $y = \log_{a} x \Rightarrow y' = \frac{1}{x \ln a} (\forall x \in (0; + \infty)) .$ Do đó:

· Với $a > 1$ ta có $(\log_{a} x)' = \frac{1}{x \ln a} > 0 \Rightarrow$ Hàm số luôn đồng biến trên khoảng $(0; + \infty) .$

Trong trường hợp này ta có: $\lim_{x \to 0^{+}} y = - \infty$ do đó đồ thị hàm số nhận trục tung là tiệm cận đứng.

· Với $0 < a < 1$ ta có: $(\log_{a} x)' = \frac{1}{x \ln a} < 0 \Rightarrow$ Hàm số luôn nghịch biến trên khoảng

· Trong trường hợp này ta có: $\lim_{x \to 0^{+}} y = + \infty$ do đó đồ thị hàm số nhận trục tung là tiệm cận đứng.

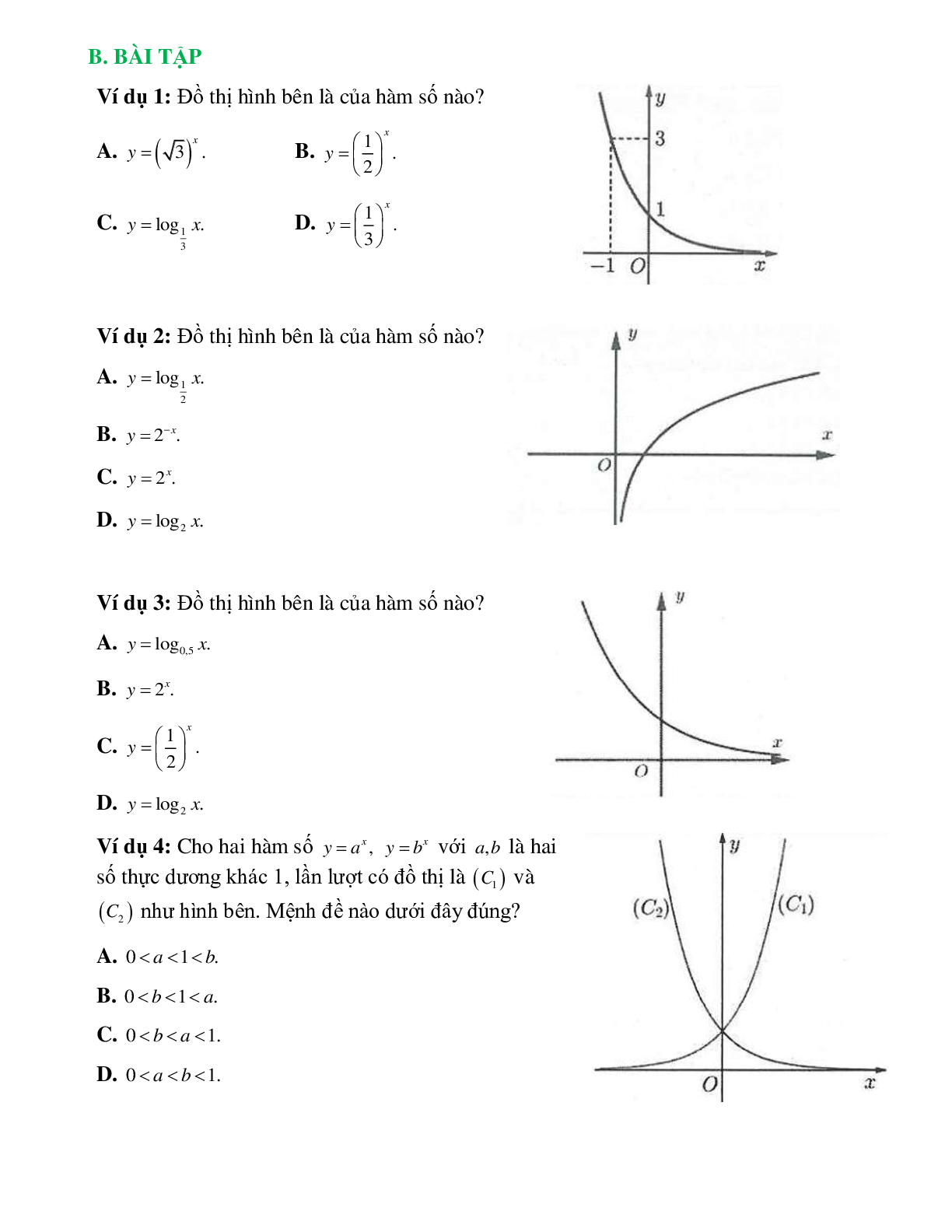
Đồ thị hàm số $y = \log_{a} x$

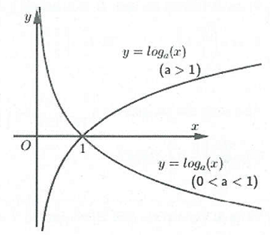
Đồ thị hàm số có tiệm cận đứng là trục $O y$ và luôn đi qua các điểm $(1; 0)$ và $(a; 1)$ và nằm phía bên phải trục tung vì có tập xác định là $D (0; + \infty) .$

Đồ thị nhận trục tung là tiệm cận đứng.

Nhận xét: Đồ thị hàm số $y = a^{x}$ và $y = \log_{a} x, (0 < a \neq 1)$ đối xứng nhau qua đường thẳng (góc phần tư thứ nhất và thứ 3 trong hệ trục tọa độ $O x y) .$