Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Hàm số lũy thừa, mũ , Logarit Toán lớp 12, tài liệu bao gồm 5 trang, tuyển chọn 10 bài tập Hàm số lũy thừa, mũ và logarit đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
HÀM SỐ LŨY THỪA, MŨ, LÔGARIT
I. Phương pháp giải
Hàm số lũy thừa \[y = {x^\alpha }:\]
Hàm số \[y = {x^\alpha }\]đồng biến trên \[\left( {0; + \infty } \right)\]khi \[\alpha > 0\]; nghịch biến trên\[\left( {0; + \infty } \right)\]khi \[\alpha < 0\].
Hàm số mũ: \[y = {a^x}:\]
Tập xác định R, nhận mọi giá trị thuộc \[\left( {0; + \infty } \right)\].
\[\mathop {\lim }\limits_{x \to + \infty } {a^x} = \left\{ \begin{array}{l} + \infty \,\,khi\,\,a > 1\\0\,\,\,\,\,\,khi\,\,0 < a < 1\end{array} \right.;\mathop {\lim }\limits_{x \to - \infty } {a^x} = \left\{ \begin{array}{l}0\,\,\,\,\,\,\,\,khi\,\,a > 1\,\\ + \infty \,\,\,\,khi\,\,0 < a < 1\end{array} \right.\]
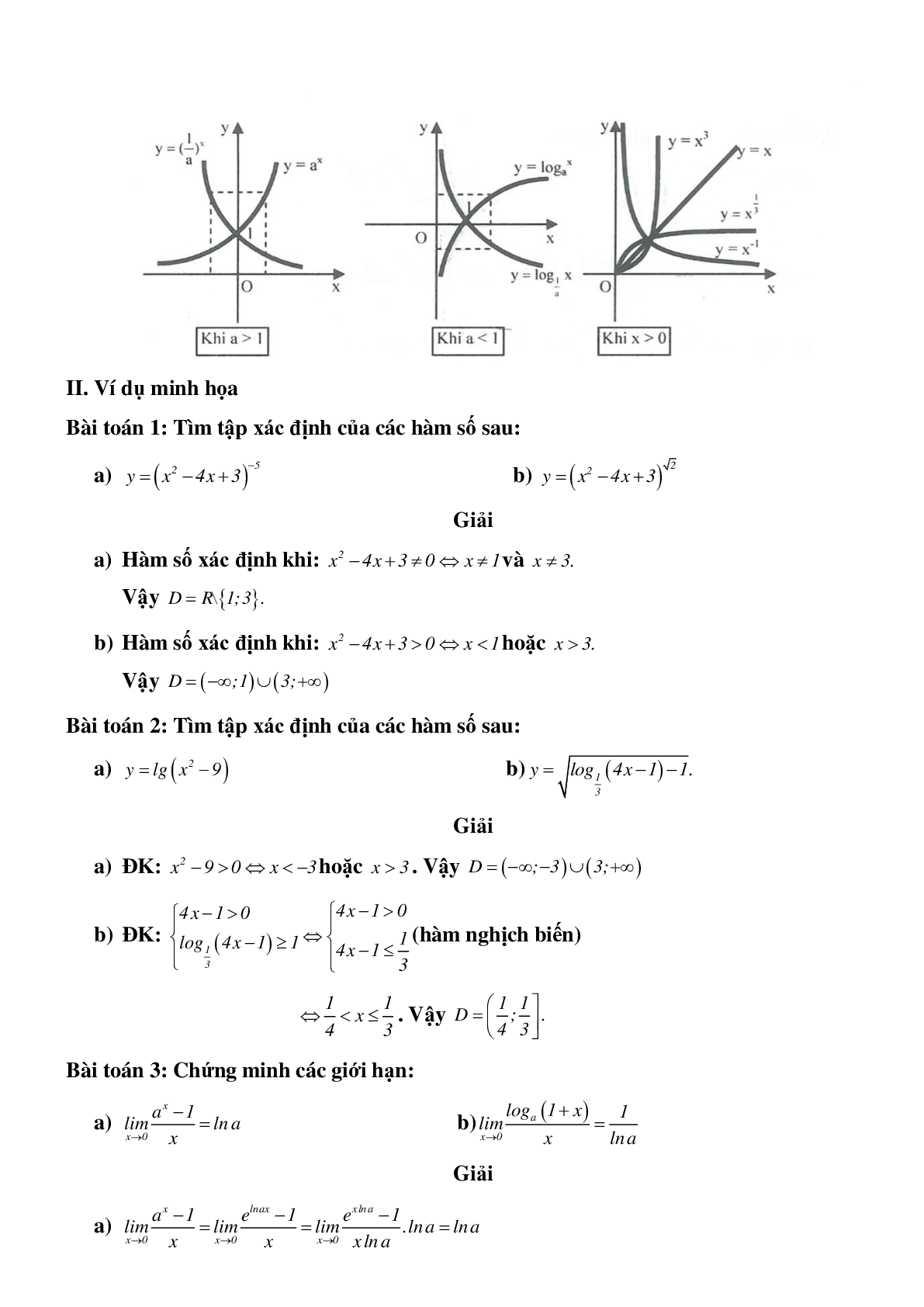
Đồng biến trên R nếu \[a > 1\], nghịch biến trên R nếu \[0 < a < 1.\]
Đồ thị luôn cắt trục tung tại điểm \[\left( {0;1} \right)\], nằm ở phía trên trục hoành và nhận trục hoành làm tiệm cận ngang.
Hàm số lôgarit \[y = {\log _a}x:\]
Liên tục trên tập xác định \[\left( {0; + \infty } \right)\], nhận mọi giá trị thuộc R.
\[\mathop {\lim }\limits_{x \to + \infty } {\log _a}x = \left\{ \begin{array}{l} + \infty \,\,khi\,a > 1\\ - \infty \,\,khi\,0 < a < 1\end{array} \right.\,;{\rm{ }}\mathop {\lim }\limits_{x \to + {0^ + }} {\log _a}x = \left\{ \begin{array}{l} - \infty \,\,khi\,a > 1\\ + \infty \,\,khi\,0 < a < 1\end{array} \right.\,\]
Hàm số \[y = {\log _a}x\]đồng biến trên \[\left( {0; + \infty } \right)\]nếu \[a < 1\], nghịch biến trên \[\left( {0; + \infty } \right)\]nếu \[0 < a < 1.\]
Đồ thị luôn cắt trục hoành tại điểm \[\left( {1;0} \right)\], nằm ở bên phải trục tung và nhận trục tung làm tiệm cận đứng.
Các giới hạn:
\[\mathop {\lim }\limits_{x \to + \infty } {\left( {1 + \mathop {\frac{1}{x}}\limits_{x \to 0} } \right)^x} = e;\mathop {{\rm{ }}\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = 1;{\rm{ }}\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{x} = 1.\]
Đồ thị và quan hệ đối xứng:
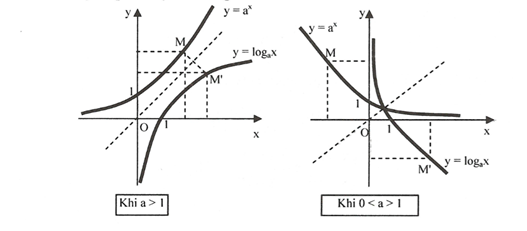
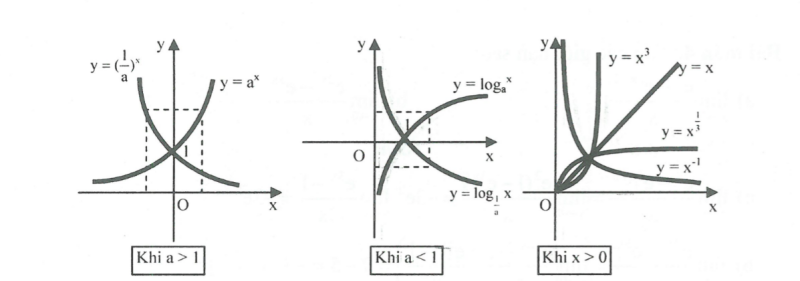
II. Ví dụ minh họa
Bài toán 1: Tìm tập xác định của các hàm số sau:
a) \[y = {\left( {{x^2} - 4x + 3} \right)^{ - 5}}\] b) \[y = {\left( {{x^2} - 4x + 3} \right)^{\sqrt 2 }}\]
Giải
a) Hàm số xác định khi: \[{x^2} - 4x + 3 \ne 0 \Leftrightarrow x \ne 1\]và \[x \ne 3.\]
Vậy \[D = R{\rm{\backslash }}\left\{ {1;3} \right\}.\]
b) Hàm số xác định khi: \[{x^2} - 4x + 3 > 0 \Leftrightarrow x < 1\]hoặc \[x > 3.\]
Vậy \[D = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\]
Bài toán 2: Tìm tập xác định của các hàm số sau:
a) \[y = \lg \left( {{x^2} - 9} \right)\] b)\[y = \sqrt {{{\log }_{\frac{1}{3}}}\left( {4x - 1} \right) - 1} .\]
Giải
a) ĐK: \[{x^2} - 9 > 0 \Leftrightarrow x < - 3\]hoặc \[x > 3\]. Vậy \[D = \left( { - \infty ; - 3} \right) \cup \left( {3; + \infty } \right)\]
b) ĐK: \[\left\{ \begin{array}{l}4x - 1 > 0\\{\log _{\frac{1}{3}}}\left( {4x - 1} \right) \ge 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 1 > 0\\4x - 1 \le \frac{1}{3}\end{array} \right.\](hàm nghịch biến)
\[ \Leftrightarrow \frac{1}{4} < x \le \frac{1}{3}\]. Vậy \[D = \left( {\frac{1}{4};\frac{1}{3}} \right].\]
Bài toán 3: Chứng minh các giới hạn:
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{{a^x} - 1}}{x} = \ln a\]
b)\[\mathop {\lim }\limits_{x \to 0} \frac{{{{\log }_a}\left( {1 + x} \right)}}{x} = \frac{1}{{\ln a}}\]
Giải
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{{a^x} - 1}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{\ln ax}} - 1}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{x\ln a}} - 1}}{{x\ln a}}.\ln a = \ln a\]
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{{{\log }_a}\left( {1 + x} \right)}}{x} = \mathop {\lim }\limits_{x \to 0} {\log _a}e\frac{{\ln \left( {1 + x} \right)}}{x} = \frac{1}{{\ln a}}\]
Bài toán 4: Tìm các giới hạn sau:
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{{e^2} - {e^{3x + 2}}}}{x}\] b) \[\mathop {\lim }\limits_{x \to 0} \frac{{{e^{2x}} - {e^{5x}}}}{x}\]
Giải
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{{e^2} - {e^{3x + 2}}}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^2}\left( {1 - {e^{3x}}} \right)}}{x} = - 3{e^2}.\mathop {\lim }\limits_{x \to 0} \frac{{{e^{3x}} - 1}}{{3x}} = - 3{e^2}\]
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{{e^{2x}} - {e^{5x}}}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{{e^{2x}} - 1}}{x} - \frac{{{e^{5x}} - 1}}{x}} \right) = 2 - 5 = - 3\]
Bài toán 5: Tìm các giới hạn sau:
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{{2^x} + {5^x} - 2}}{{{3^x} + {5^x} - 2}}\]
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{\sin 4x}}{{{e^{2x}} - {7^x}}}\]
Giải
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{{2^x} + {5^x} - 2}}{{{3^x} + {5^x} - 2}} = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{{2^x} - 1}}{x} + \frac{{{5^x} - 1}}{x}}}{{\frac{{{3^x} - 1}}{x} + \frac{{{5^x} - 1}}{x}}} = \frac{{\ln 2 + ln5}}{{\ln 3 + \ln 5}} = \frac{{\ln 10}}{{\ln 15}}\]
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{\sin 4x}}{{{e^{2x}} - {7^x}}} = \mathop {\lim }\limits_{x \to 0} \frac{{4.\frac{{\sin 4x}}{{4x}}}}{{\frac{{{e^{3x}} - 1}}{x} - \frac{{{7^x} - 1}}{x}}} = \frac{4}{{3 - \ln 7}}\].
Bài toán 6: Tìm các giới hạn sau:
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + 3x} \right)}}{x}\]
b)\[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + 3{x^2}} \right)}}{{1 - \cos 2x}}\]
Giải
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + 3x} \right)}}{x} = 3.\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + 3x} \right)}}{{3x}} = 3\]
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + 3{x^2}} \right)}}{{1 - \cos 2x}} = \mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + 3{x^2}} \right)}}{{2{{\sin }^2}x}} = \frac{1}{2}\mathop {\lim }\limits_{x \to 0} \left[ {\frac{{3\ln \left( {1 + 3{x^2}} \right)}}{{3{x^2}}}:{{\left( {\frac{{\sin x}}{x}} \right)}^2}} \right] = \frac{3}{2}\]
Bài toán 7: Tìm các giới hạn sau:
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{4x}}{{{{\log }_3}\left( {1 + 5x} \right)}}\]
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{{6^x} - {3^x}}}{{\ln \left( {1 + 6x} \right) - \ln \left( {1 + 3x} \right)}}\]
Giải
a) \[\mathop {\lim }\limits_{x \to 0} \frac{{4x}}{{{{\log }_3}\left( {1 + 5x} \right)}} = \frac{4}{{5{{\log }_3}e}}.\mathop {\lim }\limits_{x \to 0} \frac{{5x}}{{\ln \left( {1 + 5x} \right)}} = \frac{4}{5}\ln 3\]
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{{6^x} - {3^x}}}{{\ln \left( {1 + 6x} \right) - \ln \left( {1 + 3x} \right)}} = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{{6^x} - 1}}{x} - \frac{{{3^x} - 1}}{x}} \right):\left( {\frac{{\ln \left( {1 + 6x} \right)}}{x} - \frac{{\ln \left( {1 + 3x} \right)}}{x}} \right)\]
\[ = \left( {\ln 6 - \ln 3} \right):\left( {6 - 3} \right) = \frac{1}{3}\ln 2.\]
Bài toán 8: Tìm các giới hạn sau:
a) \[\mathop {\lim }\limits_{x \to + \infty } {\left( {1 + \frac{1}{{x - 3}}} \right)^x}\]
b) \[\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{{x + 3}}{{x + 1}}} \right)^x}\]
Giải
a) \[\mathop {\lim }\limits_{x \to + \infty } {\left( {1 + \frac{1}{{x - 3}}} \right)^x} = \mathop {\lim }\limits_{x \to + \infty } {\left[ {{{\left( {1 + \frac{1}{{x - 3}}} \right)}^{x - 3}}} \right]^{\frac{x}{{x - 3}}}} = {e^1} = e\]
b) \[\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{{x + 3}}{{x + 1}}} \right)^x} = \mathop {\lim }\limits_{x \to + \infty } {\left( {1 + \frac{2}{{x + 1}}} \right)^x} = \mathop {\lim }\limits_{x \to + \infty } {\left[ {{{\left( {1 + \frac{1}{{\frac{{x + 1}}{2}}}} \right)}^{\frac{{x + 1}}{2}}}} \right]^{\frac{{2x}}{{x + 1}}}} = {e^2}\].
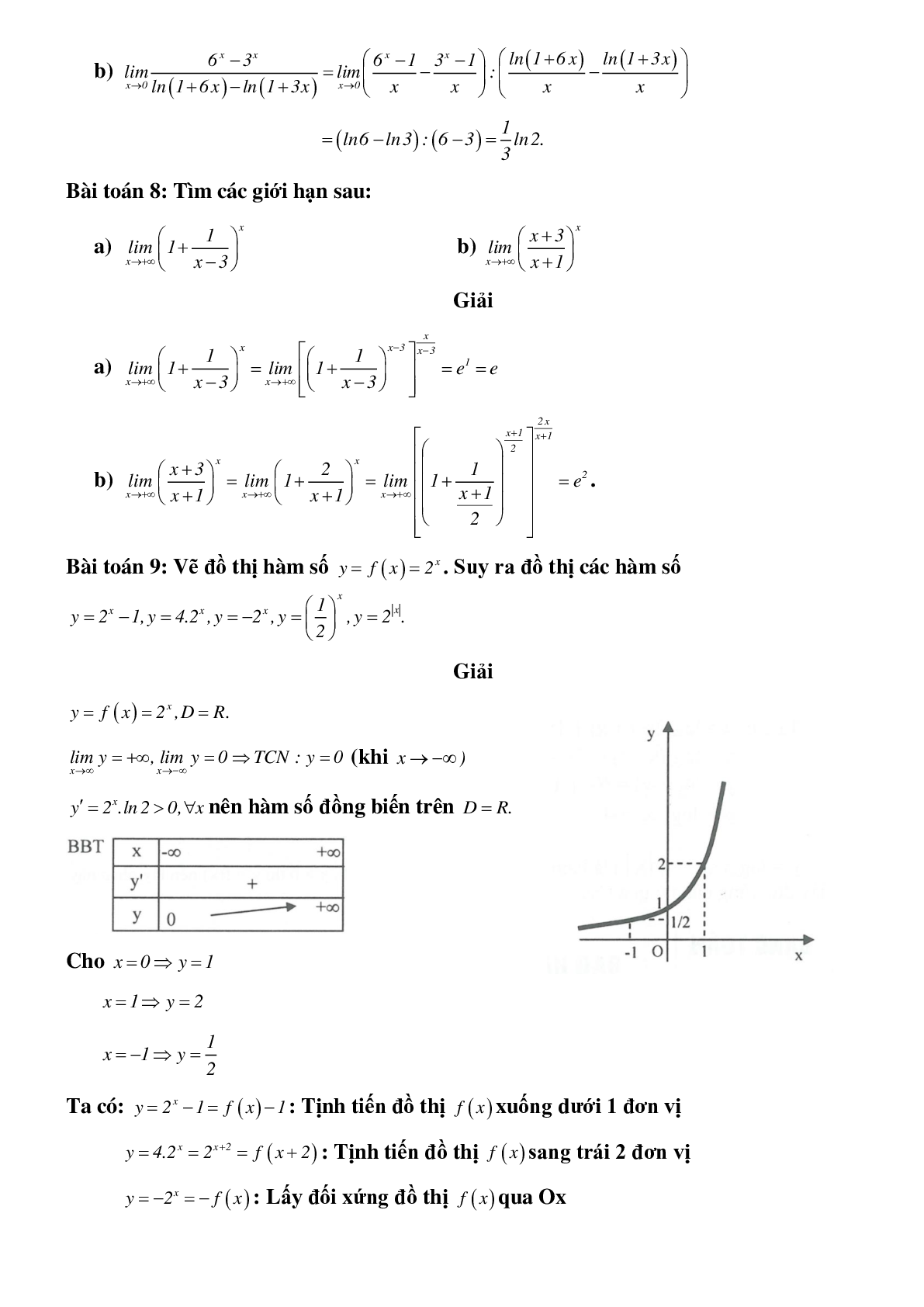
Bài toán 9: Vẽ đồ thị hàm số \[y = f\left( x \right) = {2^x}\]. Suy ra đồ thị các hàm số \[y = {2^x} - 1,y = {4.2^x},y = - {2^x},y = {\left( {\frac{1}{2}} \right)^x},y = {2^{\left| x \right|}}.\]
Giải
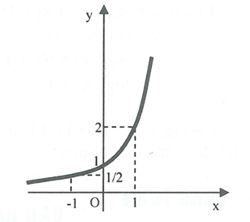
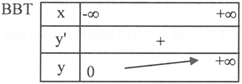
\[y = f\left( x \right) = {2^x},D = R.\]
\[\mathop {\lim }\limits_{x \to \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = 0 \Rightarrow TCN:y = 0\] (khi \[x \to - \infty )\]
\[y' = {2^x}.\ln 2 > 0,\forall x\]nên hàm số đồng biến trên \[D = R.\]
Cho \[x = 0 \Rightarrow y = 1\]
\[x = 1 \Rightarrow y = 2\]
\[x = - 1 \Rightarrow y = \frac{1}{2}\]
Ta có: \[y = {2^x} - 1 = f\left( x \right) - 1\]: Tịnh tiến đồ thị \[f\left( x \right)\]xuống dưới 1 đơn vị
\[y = {4.2^x} = {2^{x + 2}} = f\left( {x + 2} \right)\]: Tịnh tiến đồ thị \[f\left( x \right)\]sang trái 2 đơn vị
\[y = - {2^x} = - f\left( x \right)\]: Lấy đối xứng đồ thị \[f\left( x \right)\]qua Ox
\[y = {\left( {\frac{1}{2}} \right)^x} = {2^{ - x}} = f\left( { - x} \right)\]: Lấy đối xứng đồ thị \[f\left( x \right)\]qua Oy.
\[y = {2^{\left| x \right|}} = f\left( {\left| x \right|} \right)\] hàm số chẵn, khi \[x \ge 0\]thì \[y = f\left( x \right)\]nên lấy phần này và lấy đối xứng của nó qua Oy.
Bài toán 10: Vẽ đồ thị hàm số \[y = f\left( x \right) = {\log _2}x.\]
Suy ra các đồ thị hàm số
Giải
\[y = f\left( x \right) = {\log _2}x,D = \left( {0; + \infty } \right)\]
\[\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to {0^ + }} y = - \infty \Rightarrow \]TCĐ:\[x = 0\](khi \[x \to {0^ + }\])
\[y' = \frac{1}{{x\ln 2}} > 0,\forall x > 0\]nên hàm số đồng biến trên \[\left( {0; + \infty } \right).\]
BBT:
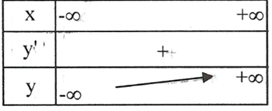
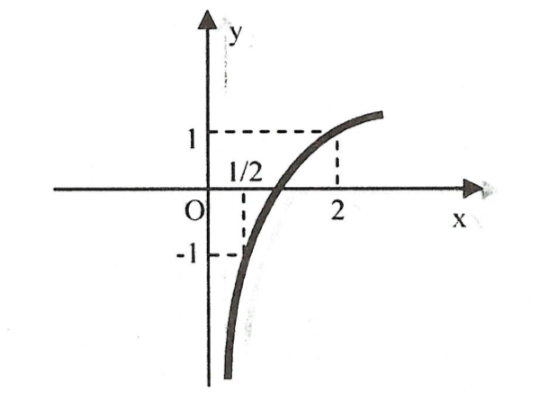
Cho \[x = \frac{1}{2} \Rightarrow y = - 1\]
\[x = 1 \Rightarrow y = 0,x = 2 \Rightarrow y = 1\]
Ta có: \[y = {\log _2}2x = f\left( x \right) + 1\]: Tịnh tiến đồ thị \[f\left( x \right)\]lên trên 1 đơn vị
\[y = {\log _2}\left( {x - 3} \right) = f\left( {x - 3} \right)\]: Tịnh tiến đồ thị \[f\left( x \right)\]sang phải 3 đơn vị
\[y = {\log _2}\left( { - x} \right) = f\left( { - x} \right)\]: Lấy đối xứng đồ thị \[f\left( x \right)\]qua Oy
\[y = {\log _{\frac{1}{2}}}x = - f\left( x \right)\]: Lấy đối xứng đồ thị \[f\left( x \right)\]qua Ox
\[y = {\log _2}\left| x \right| = f\left( {\left| x \right|} \right)\]là hàm số chẵn, khi \[x > 0\]thì \[y = f\left( x \right)\]nên lấy phần này và lấy đối xứng của nó qua Oy.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
