Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Vận dụng cao - Phương trình Mũ - Logarit trong đề thi thử THPTQG năm 2021, tài liệu bao gồm 17 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Vận dụng cao - Phương trình Mũ - Logarit trong đề thi thử THPTQG năm 2021 có lời giải chi tiết

Câu 1.  Có bao nhiêu số nguyên a ( a ³ 2) sao cho tồn tại số thực x thỏa mãn \[{\left( {{a^{\log x}} + 2} \right)^{\log a}} = x - 2\]?

A. 8.

B. 9.

C. 1.

D. Vô số

Lời giải

Điều kiện x > 0. Đặt y = a^logx + 2 > 0 thì y^loga = x – 2 Û a^loga + 2 = x.

Từ đó ta có hệ

\[\left\{ {\begin{array}{*{20}{c}}{y = {a^{\log x}} + 2}\\{x = {a^{\log y}} + 2}\end{array}.} \right.\]

Do a ³ 2 nên hàm số f(t) = a^t + 2 là đồng biến trên \[\mathbb{R}\]. Giả sử x ³ y thì f(y) ³ f(x) sẽ kéo theo y ³ x, tức là phải có x = y . Tương tự nếu x £ y.

Vì thế, ta đưa về xét phương trình x = a^logx + 2 với x > 0 hay x – x^loga = 2.

Ta phải có x > 2 và x > x^loga Û 1 > log a Û a < 10.

Ngược lại, với a <10 thì xét hàm số liên tục g(x) = x – x^loga – 2 = x^loga (x^1-loga – 1) – 2 có

\[\mathop {\lim }\limits_{x \to  + \infty } g(x) =  + \infty \] và g(2) < 0.

Nên g(x) sẽ có nghiệm trên (2; +¥). Do đó, mọi số a Î{2,3,…,9} đều thỏa mãn.

Câu 2: Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để phương trình \[{\log _2}\left( {m + \sqrt {m + {2^x}} } \right) = 2x\] có nghiệm thực?

A. 2018 .

B. 2019 .

C. 2021.

D. 2020 .

Lời giải

Chọn D

Ta có phương trình: \[{\log _2}\left( {m + \sqrt {m + {2^x}} } \right) = 2x\] (1)

Đặt: \[t = \sqrt {m + {2^x}} (t \ge 0)\] thì phương trình (1) trở thành

\[ \Leftrightarrow {\log _2}\left( {m + t} \right) = 2x \Leftrightarrow m + t = {4^x} \Leftrightarrow t = {4^x} - m\]

Mà \[t = \sqrt {m + {2^x}} \] nên suy ra

\[\begin{array}{l}{4^x} - m = \sqrt {{2^x} + m}  \Leftrightarrow {4^x} = \sqrt {{2^x} + m}  + m\\ \Rightarrow {4^x} + {2^x} = \sqrt {{2^x} + m}  + {2^x} + m\end{array}\]

Từ đây ta xét hàm đặc trưng

 y = f(t) = t² + t, " t ³ 0 có \[f'(t) = 2t + 1 > 0,\forall t \ge 0\]

Þ f(t) đồng biến trên [0;+¥)

 Þ f(2^x) = \[f\left( {\sqrt {{2^x} + m} } \right) \Leftrightarrow {2^x} = \sqrt {{2^x} + m}  \Leftrightarrow m = {4^x} - {2^x}\]

Xét hàm y = g(x) = 4^x – 2^x

có \[g'(x) = {4^x}.2\ln (2) - {2^x}\ln (2) = 0 \Leftrightarrow x =  - 1\]

Ta có bảng biến thiên của hàm g(x) như sau:

Từ đó để phương trình trên có 2 nghiệm thực thì m > g(-1) Þ \[m >  - \frac{1}{4}\]

Mà m nguyên dương và nhỏ hơn 2021nên suy ra mÎ[1;2020]

Vậy có tất cả 2020 giá trị nguyên m thỏa mãn yêu cầu đề bài.

Câu 3: Tính tổng S tất cả các nghiệm của phương trình \[\ln \left( {\frac{{{5^x} + {3^x}}}{{6x + 2}}} \right) + {5^{x + 1}} + {5.3^x} - 30x - 10 = 0.\]

A. S = 3.

B. S =1.

C. S = 2 .

D. S = -1.

Lời giải

Chọn B.

Ta có:

 \[\begin{array}{l}\ln \left( {\frac{{{5^x} + {3^x}}}{{6x + 2}}} \right) + {5^{x + 1}} + {5.3^x} - 30x - 10 = 0\\ \Leftrightarrow \ln \left( {{5^x} + {3^x}} \right) + 5\left( {{5^x} + {3^x}} \right) = \ln (6x + 2) + 5(6x + 2).\end{array}\]

Khi đó phương trình có dạng f(5^x + 3^x) = f (6x + 2), với f(t) = ln t +5t, t Î (0; +¥)

\[ \Rightarrow f'(t) = \frac{1}{t} + 5 > 0,\forall t \in \left( {0; + \infty } \right)\]Þ f(t) đồng biến trên (0; +¥) nên từ phương trình

f(5^x + 3^x) = f(6x + 2) Þ5^x + 3^x = 6x + 2 Þ g(x) = 5^x + 3^x - 6x – 2 = 0.

\[g'(x) = {5^x}\ln 5 + {3^x}\ln 3 - 6 \Rightarrow g''(x) = {5^x}{(\ln 5)^2} + {3^x}{(\ln 3)^3} > 0,\forall x\]

Do \[g''(x) > 0,\forall x\]Þ phương trình \[g'(x)\]= 0 có nhiều nhất là một nghiệm, từ đó phương trình g(x) = 0 có nhiều nhất là hai nghiệm. Ta thấy x₁ = 0; x₂ = 1 là hai nghiệm của phương trình g(x) = 0.

Vậy phương trình có hai nghiệm là x₁ = 0; x₂ = 1 Þ S = x₁ + x₂ = 1.

Câu 4: Gọi S là các cặp số thực (x;y) sao cho ln(x-y)^x – 2020x = ln(x- y)^y -2020y +e²⁰²¹ và x Î [-1;1]. Biết rằng giá trị lớn nhất của biểu thức \[P = {e^{2021x}}(y + 1) - 2021{x^2}\] với (x;y) Î S đạt được tại (x₀;y₀). Mệnh đề nào sau đây đúng?

A. \[{x_0} \in \left[ {\frac{1}{2};1} \right]\]

B. \[{x_0} \in \left[ {\frac{1}{4};\frac{1}{2}} \right]\]

C. \[{x_0} \in \left[ { - 1;0} \right)\]

D. \[{x_0} \in \left[ {0;\frac{1}{4}} \right)\]

Lời giải

Chọn A

Điều kiện x - y  > 0

Ta có ln(x – y)^x – 2020x = ln(x – y)^y – 2020y + e²⁰²¹

Û (x – y)ln(x – y) - 2020(x – y) = e²⁰²¹

Û ln(x – y) – 2020 - \[\frac{{{e^{2021}}}}{{x - y}} = 0(*)\]

Xét hàm f(t) = lnt – 2020 - \[\frac{{{e^{2021}}}}{{x - y}} = 0,\]có \[f'(t) = \frac{1}{t} + \frac{{{e^{2021}}}}{t} > 0,\forall t > 0\]

Do đó f(t) đồng biến trên khoảng (0;+ ¥)

Suy ra (*) Û f(x – y) = 0 = f(e²⁰²¹) Û x – y = e²⁰²¹ Ûy=x - e²⁰²¹

Khi đó P = e^2021x (1 + x - e²⁰²¹) – 2021x² = g(x)

\[\begin{array}{l}g'(x) = {e^{2021x}}(2022 + 2021x - 2021{e^{2021}}) - 4042x\\g''(x) = {e^{2021x}}(2021.2022 + {2021^2}x - {2021^2}{e^{2021}}) - 4042\\ \le {e^{2021x}}(2021.2022 + {2021^2}x - {2021^2}{e^{2021}}) - 4042 < 0,\forall x \in \left[ { - 1;1} \right]\end{array}\]

Nếu \[g'(x)\] nghịch biến trên đoạn [-1;1]

Mà  \[g'( - 1) = {e^{ - 2021}} + 2021 > 0,g'(0) = 2022 - 2021{e^{2021}} < 0\] nên tồn tại x₀ Î ( -1;0) sao cho g(x₀) = 0 và khi đó \[\mathop {Max}\limits_{\left[ {1;1} \right]} g(x) = g({x_0})\] . Vậy P lớn nhất tại x₀ Î ( -1;0).

Câu 5: Cho x,y 0 > thỏa 2xy + log₂(xy + x)^x = 8. Giá trị nhỏ nhất của P = x² + y

A. \[\frac{{14\sqrt 3  - 10}}{7}\]

B. \[2\sqrt 3  - 1\]

C. \[3\sqrt[3]{4} - 1\]

D. \[4\sqrt[3]{3} - 3\]

Lời giải

Chọn C

Ta có:

2xy + log₂(xy +x)^x = 8 Û 2xy + log₂ [x(y + 1)]^x = 8

\[\begin{array}{l} \Leftrightarrow 2y + {\log _2}(y + 1) = \frac{8}{x} - {\log _2}x\\ \Leftrightarrow {\log _2}(y + 1) + 2(y + 1) = \frac{8}{x} + 2 - {\log _2}x\\ \Leftrightarrow {\log _2}(y + 1) + 2(y + 1) = {\log _2}\left( {\frac{4}{x}} \right) + 2.\left( {\frac{4}{x}} \right)\end{array}\]

Xét hàm y = f(t) = log₂t + 2t, " t > 0 có \[f'(t) = \frac{1}{{t.\ln 2}} + 2 > 0,\forall t > 0\]

Suy ra hàm f(t) luôn đồng biến trên (0; +¥)

Do đó : f(y + 1) = \[f\left( {\frac{4}{x}} \right) \Leftrightarrow y + 1 = \frac{4}{x}\]

Khi đó ta có: P = x² + y = x² + \[\frac{4}{x}\] - 1

 = x² + \[\frac{2}{x}\]+ \[\frac{2}{x}\] - 1 \[ \ge 3\sqrt[3]{{{x^2}.\frac{2}{x}.\frac{2}{x}}} - 1 = 3\sqrt[3]{4} - 1\]

Vậy giá trị nhỏ nhất của P = x² + y là \[3\sqrt[3]{4} - 1\] khi và chỉ khi x² = \[\frac{2}{x} \Leftrightarrow x = \sqrt[3]{2}\]

Câu 6: ) Số các giá trị nguyên nhỏ hơn 2021 của tham số m để phương trình log₆ (2020x + m) = log₄ (1010x) có nghiệm là

A. 2021.

B. 2023.

C. 2022 .

D. 2024 .

Lời giải

Chọn B.

Điều kiện xác định: \[\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{x > \frac{{ - m}}{{2020}}}\end{array}} \right.\].

Đặt log₆ (2020 + m) = log₄(1010x) = t

Þ \[\left\{ {\begin{array}{*{20}{c}}{2020x + m = {6^t}}\\{1010x = {4^t}}\end{array}} \right. \Rightarrow m = {6^t} - {2.4^t}(1).\]

Xét hàm số f(t) = 6^t – 2.4^t với \[\forall t \in \mathbb{R}\]

\[\begin{array}{l}f'(t) = {6^t}.\ln 6 - {2.4^t}.\ln 4\\f'(t) = 0 \Leftrightarrow {\left( {\frac{3}{2}} \right)^t} = 2\frac{{\ln 4}}{{\ln 6}} \Leftrightarrow t = {\log _{\frac{3}{2}}}({\log _6}16).\end{array}\]

Bảng biến thiên:

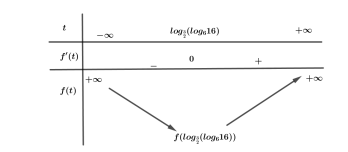
Phương trình đã cho có nghiệm khi và chỉ khi phương trình (1) có nghiệm. Từ bảng biến thiên ta thấy phương trình có nghiệm khi \[m \ge f\left( {{{\log }_{\frac{3}{2}}}\left( {{{\log }_6}16} \right)} \right) \Rightarrow  - 2 \le m < 2021.\]

Vậy có 2023 giá trị của m thỏa mãn ycbt.

Câu 7: Cho hai số thực a >1; b >1 , biết phương trình \[{a^x}{b^{{x^2} - 1}} = 1\] có hai nghiệm x₁ ,x₂. Tìm giá trị nhỏ nhất của biểu thức \[S = {\left( {\frac{{{x_1}{x_2}}}{{{x_1} + {x_2}}}} \right)^2} - 4({x_1} + {x_2})\]

A. 4.

B. \[\sqrt[3]{4}.\]

C. \[3\sqrt[3]{4}.\]

D. \[3\sqrt[3]{2}.\]

Lời giải

Chọn C.

Ta có: \[{a^x}{b^{{x^2} - 1}} = 1 \Leftrightarrow {\log _b}({a^x}{b^{{x^2} - 1}}) = {\log _b}1 \Leftrightarrow {x^2} + x{\log _b}a - 1 = 0\]

Phương trình có hai nghiệm x₁ ,x₂ theo viet ta có: \[\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} =  - {{\log }_b}a}\\{{x_1}.{x_2} =  - 1}\end{array}} \right.\]

\[S = {\left( {\frac{{{x_1}{x_2}}}{{{x_1} + {x_2}}}} \right)^2} - 4({x_1} + {x_2}) = {\left( {{{\log }_a}b} \right)^2} + \frac{4}{{{{\log }_a}b}}.\]

Đặt log_ab = t, t > 0.

\[S = f(t) = {t^2} + \frac{4}{t}\] với t > 0.

Ta có:

\[\begin{array}{l}f'(t) = 2t - \frac{4}{{{t^2}}}\\f'(t) = 0 \Leftrightarrow \frac{{2{t^3} - 4}}{{{t^2}}} = 0 \Leftrightarrow t = \sqrt[3]{2}.\end{array}\]

Bảng biến thiên:

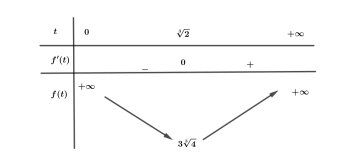
Dựa vào bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số f(t) trên khoảng (0;+¥) bằng \[f\left( {\sqrt[3]{2}} \right) = 3\sqrt[3]{4}.\]

Vậy giá trị nhỏ nhất của S bằng \[3\sqrt[3]{4}\].