Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 57 bài toán vận dụng - vận dụng cao hàm số mũ, logarit, tài liệu bao gồm 38 trang, 57 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tuyển tập 57 câu hỏi vận dụng – vận dụng cao từ các đề thi thử trên cả nước năm 2019 – có đáp án chi tiết thực hiện giải bởi tập thể giáo viên Diễn Đàng Giáo Viên Toán.

HÀM SỐ MŨ – LOGARIT

Câu 1. Giá trị thực của tham số \(m\) để phương trình \({4^x} - (2m + 3) \cdot {2^x} + 64 = 0\) có hai nghiệm thực \({x_1}\), \({x_2}\) thóa mãn \(\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 24\) thuộc khoảng nào sau đây?

A. \(\left( {0;\frac{3}{2}} \right)\).

B. \(\left( { - \frac{3}{2};0} \right)\).

C. \(\left( {\frac{{21}}{2};\frac{{29}}{2}} \right)\).

D. \(\left( {\frac{{11}}{2};\frac{{19}}{2}} \right)\).

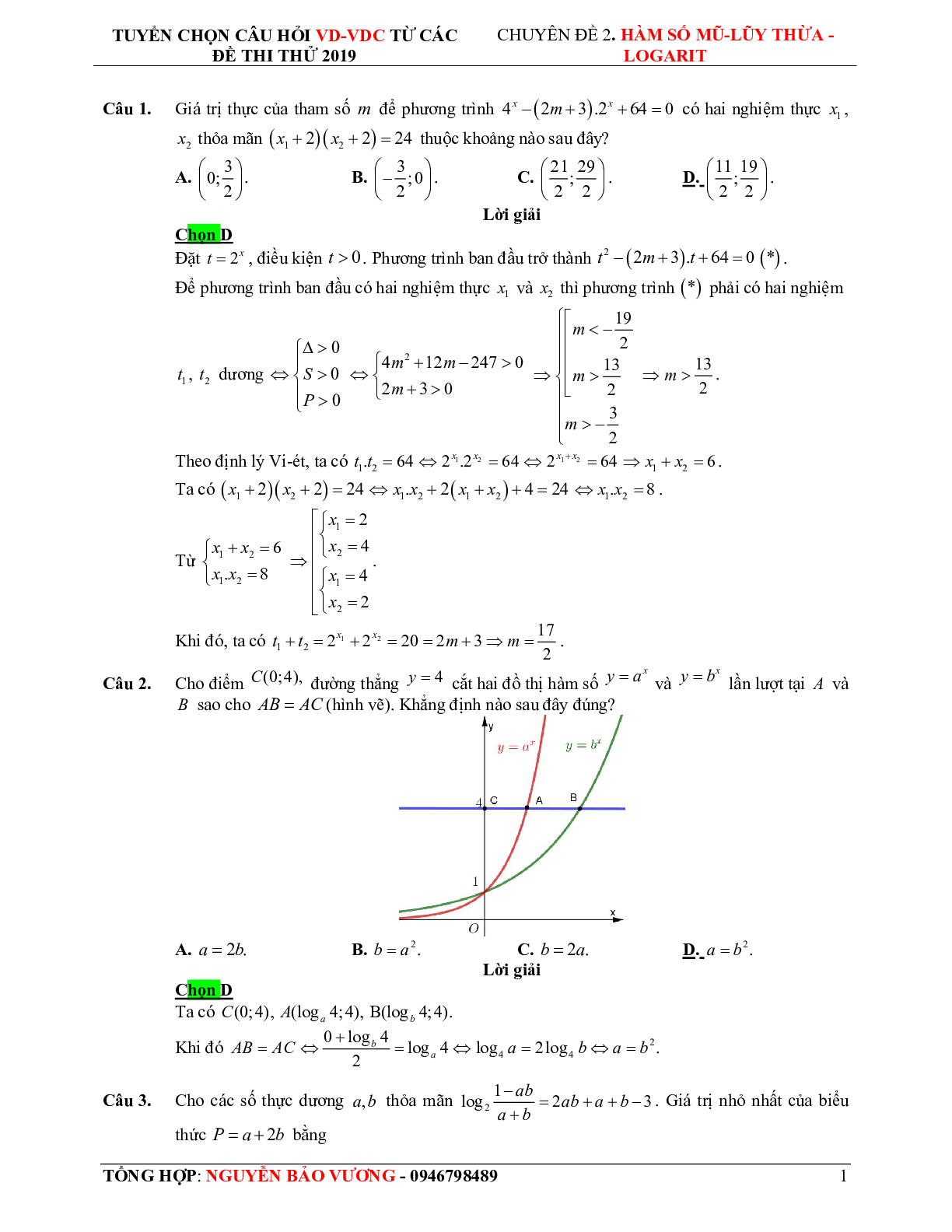
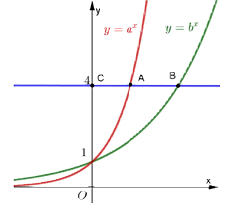
Câu 2. Cho điểm C(0 ; 4), đường thẳng y=4 cắt hai đồ thị hàm số \(y = {a^x}\) và \(y = {b^x}\) lần lượt tại A và B sao cho  B=AC (hình vẽ). Khẳng định nào sau đây đúng?

Câu 3. Cho các số thực dương a, b thỏa mãn \({\log _2}\frac{{1 - ab}}{{a + b}} = 2ab + a + b - 3\). Giá trị nhỏ nhất của biểu thức P=a+2b bằng

A. \(\frac{{2\sqrt {10}  - 1}}{2}\).

B. \(\frac{{2\sqrt {10}  - 3}}{2}\).

C. \(\frac{{3\sqrt {10}  - 7}}{2}\).

D. \(\frac{{2\sqrt {10}  - 5}}{2}\).

Câu 4. Gọi S là tập hợp tất cá các giá trị nguyên của tham số m để phương trình \({5^x} + 10 = m\sqrt {{{25}^x} + 4} \) có nghiệm duy nhất. Số tập con của S là

A. 3.

B. 4.

C. 16.

D. 15.

Câu 5. Anh \({\rm{X}}\) muốn mua một chiếc xe máy Yamaha Exciter 150 giá 47.500 .000 của cửa hàng Phú Tài nhưng vì chưa đủ tiền nên anh \({\rm{X}}\) đã quyết định mua theo hình thức như sau: trả trước 25 triệu đồng và trả góp trong 12 tháng, với lãi suất \(0.6\% \) tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho cửa hàng Phú Tài số tiền là bao nhiêu(quy tròn đến hàng đơn vi).

A. 1.948 .927 đồng.

B. 1.948 .926 đồng.

C. 2.014 .545 đồng.

D. 2.014 .546 đồng.

Câu 6. Biết rằng bất phương trình \({\log _2}\left( {{5^x} + 2} \right) + 2 \cdot {\log _{\left( {{5^x} + 2} \right)}}2 > 3\) có tập nghiệm là \(S = \left( {{{\log }_a}b; + \infty } \right)\), với a,b là các số nguyên dương nhỏ hơn 6 và \(a \ne 1\). Tính P=2a+3b.

A. P=7.

B. P=11.

C. P=18.

D. P=16.

Câu 7. Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất \(7\% \) năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo và từ năm thứ 2 trớ đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng. Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt thời gian gữi lãi suất không thay đổi và ông Chính không rút tiền ra (kết quả được làm tròn đến hàng nghìn).

A. 1.686.898.000 VNĐ.

B. 743.585 .000 VNĐ.

C. 739.163 .000 VNĐ.

D. 1.335 .967 .000 VNĐ.

Câu 8. Cho a, b là hai số thực dương thỏa mãn \({\log _5}\left( {\frac{{4a + 2b + 5}}{{a + b}}} \right) = a + 3b - 4\). Tìm giá trị nhỏ nhất của biểu thức \(T = {a^2} + {b^2}\)

A. \(\frac{1}{2}\).

B. 1 .

C. \(\frac{3}{2}\).

D. \(\frac{5}{2}\).

Câu 9. Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả sử 1 tế bào E. Coli khối lượng khoảng \(15 \cdot {10^{ - 15}}\;{\rm{g}}\). Hỏi sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là bao nhiêu? (chọn đáp án chính xác nhất).

A. \(2,34 \cdot {10^{29}}(g)\).

B. \(3,36 \cdot {10^{29}}(g)\).

C. \(2,25 \cdot {10^{26}}(\;{\rm{kg}})\).

D. \(3,35 \cdot {10^{26}}(\;{\rm{kg}})\).

Câu 10. Gọi n là số nguyên dương sao cho \(\frac{1}{{{{\log }_3}x}} + \frac{1}{{{{\log }_{{3^2}}}x}} + \frac{1}{{{{\log }_{{3^3}}}x}} +  \ldots  + \frac{1}{{{{\log }_{{3^n}}}x}} = \frac{{190}}{{{{\log }_3}x}}\) đúng với mọi x dương, \(x \ne 1\). Tìm giá trị của biểu thức P=2n+3.

A. P=32.

B. P=23.

C. P=43.

D. P=41.

Câu 11. Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn \({\log _{{x^2} + {y^2} + 2}}\left( {4x + 4y - 6 + {m^2}} \right) \ge 1\) và \({x^2} + {y^2} + 2x - 4y + 1 = 0\).

A. \(S = \{  - 5; - 1;1;5\} \).

B. \(S = \{  - 1;1\} \).

C. \(S = \{  - 5;5\} \).

D. \(S = \{  - 7 - 5; - 1;1;5;7\} \).

Câu 12. Tìm tất cả các giá trị thực của tham số m để phương trình \({e^{3m}} + {e^m} = 2\left( {x + \sqrt {1 - {x^2}} } \right)\left( {1 + x\sqrt {1 - {x^2}} } \right)\) có nghiệm.

A. \(\left( {0;\frac{1}{e}} \right)\)

B. \(\left( {0;\frac{1}{2}\ln 2} \right)\).

C. \(\left( { - \infty ;\frac{1}{2}\ln 2} \right]\).

D. \(\left[ {\frac{1}{2}\ln 2; + \infty } \right)\).

Câu 13. Cho x, y là hai số thực dương thoả mãn \({\log _{\frac{1}{2}}}x + {\log _{\frac{1}{2}}}y \le {\log _{\frac{1}{2}}}\left( {x + {y^2}} \right)\). Tìm giá trị nhó nhất \({P_{\min }}\) của biểu thức P=3x+y.

A. \({P_{\min }} = 8\).

B. \({P_{\min }} = \frac{{17}}{2}\).

C. \({P_{\min }} = \frac{{25\sqrt 2 }}{4}\).

D. \({P_{\min }} = 9\).

Câu 14. Một người vay ngân hàng 90.000 .000 đồng theo hình thức trả góp trong 3 năm, mỗi tháng người đó phải trả số tiền gốc là như nhau và tiền lãi. Giả sử lãi suất không thay đổi trong toàn bộ quá trình trả nợ là \(0.8\% \) trên tháng. Tổng số tiền mà người đó phải trả cho ngân hàng trong toàn bộ quá trình trả nợ là

A. 103.120 .000 đồng.

B. 103.420 .000 đồng.

C. 103.220 .000 đồng.

D. 103.320 .000 đồng.

Câu 15. Cho hai số thực a, b thỏa mãn \({a^2} + {b^2} > 1\) và \({\log _{{a^2} + {b^2}}}(a + b) \ge 1\). Giá trị lớn nhất của biểu thức P=2a+4b-3 là

A. \(\sqrt {10} \).

B. \(\frac{{\sqrt {10} }}{2}\).

C. \(2\sqrt {10} \)

D. \(\frac{1}{{\sqrt {10} }}\).

Câu 16. Một thầy giáo cứ đầu mỗi tháng lại gưi ngân hàng 8000000 VNĐ với lãi suất \(0,5\% \) / tháng. Hỏi sau bao nhiêu tháng thầy giáo có thể tiết kiệm tiền để mua được một chiếc xe ô tô trị giá 400000000 VNÐ ?

A. 60 .

B. 50 .

C. 55 .

D. 45 .

Câu 17. Tích các nghiệm của phương trình \({\log _x}(125x) \cdot \log _{25}^2x = 1\)

A. 630 .

B. \(\frac{1}{{125}}\).

C. \(\frac{{630}}{{625}}\).

D. \(\frac{7}{{125}}\)

Câu 18. Gọi x, y là các số thụ̣c dương thỏa mãn điều kiện \({\log _9}x = {\log _6}y = {\log _4}(x + y)\) và \(\frac{x}{y} = \frac{{ - a + \sqrt b }}{2}\), với a, b là hai số nguyên dương. Tính \(T = {a^2} + {b^2}\).

A. \(T = 26\).

B. \(T = 29\).

C. \(T = 20\).

D. \(T = 25\).

Câu 19. Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất \(0,7\% /\) tháng với tổng số tiền vay là 1 tỉ đồng. Giả sử mỗi tháng ba người đều trả cho ngân hàng một số tiền như nhau đề trừ vào tiền gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần 10 tháng, Bình cần 15 tháng và Cường cần 25 tháng. Hỏi tổng số tiền mà ba anh em trả ở tháng thứ nhất cho ngân hàng là bao nhiêu (làm tròn đến hàng nghìn)?

A. 6426800 .

B. 45672000 .

C. 46712000 .

D. 63271000 .

Câu 20. Tìm tất cả các giá trị của tham số m để bất phương trình \({4^{x - 1}} - m\left( {{2^x} + 1} \right) > 0\) nghiệm đúng với mọi \(x \in \mathbb{R}\).

A. \(m \in ( - \infty ;0]\).

B. \(m \in (0; + \infty )\).

C. \(m \in (0;1)\).

D. \(m \in ( - \infty ;0) \cup (1; + \infty )\).

Câu 21. Với mọi số thực x, y thỏa điều kiện \({\log _2}\left( {\frac{{xy + 1}}{{{x^2} + {y^2}}}} \right) = 2\left( {{x^2} + {y^2}} \right) - xy\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = \frac{{{x^4} + {y^4}}}{{2xy + 1}}\). Tính giá trị biểu thức \(Q = 15m + 2{\log _2}M\).

A. Q=0.

B. Q=1.

C. Q=-2.

D. Q=-1.

Câu 22. Cho \(a{\log _{2019}}9 + b{\log _{2019}}673 = 2018\) với \(a,b \in \mathbb{N}\). Khẳng định nào đúng trong các khẳng định sau đây?

A. \(b = 2a\).

B. \(b = {a^2}\).

C. \(a = {b^2}\).

D. \(a = 2b\).

Câu 23. Cho hai số thực x, y thay đổi thỏa mãn đẳng thức \(\frac{{{x^2} \cdot {2^{{x^2} + 1}}}}{{x - 1}} + (y - 1) \cdot {2^{x + y - xy}} = 0\). Tìm giá trị lớn nhất M của y, biết rằng x>1.

A. \(M =  - \frac{7}{2}\).

B. M=-3.

C. M=1.

D. M=0.

Câu 24. Cho a, b là các số dương thỏa mãn \({\log _9}a = {\log _{16}}b = {\log _{12}}\frac{{5b - a}}{2}\). Giá trị của \(\frac{a}{b}\) bằng

A. \(\frac{a}{b} =  - 1 + \sqrt 6 \).

B. \(\frac{a}{b} = \frac{{7 + 2\sqrt 6 }}{{25}}\).

C. \(\frac{a}{b} = \frac{{1 + \sqrt 6 }}{5}\).

D. \(\frac{a}{b} = 7 - 2\sqrt 6 \).

Câu 25. Tìm tất cả các giá trị thực của tham số m để phương trình \({4^x} + {2^x} + 4 = {3^m}\left( {{2^x} + 1} \right)\) có hai nghiệm phân biệt.

A. \(1 < m \le {\log _3}4\).

B. \({\log _4}3 \le m < 1\).

C. \(1 < m < {\log _3}4\).

D. \({\log _4}3 < m < 1\).

Câu 26. Cho phương trình \({5^x} + m = {\log _5}(x - m)\) với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m \in ( - 20;20)\) để phương trình đã cho có nghiệm?

A. 20 .

B. 21 .

C. 9 .

D. 19 .

Câu 27. Nhằm tạo môi trường xanh, sạch, đẹp và thân thiện. Đoàn trường THPT Hậu Lộc 2 đã phát động phong trào trồng hoa toàn bộ khuôn viên đường vào trường. Sau một ngày thực hiện đã trồng được một phần diện tích. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 ngày nữa sẽ hoàn thành. Nhưng thấy công việc có ý nghĩa nên mỗi ngày số lượng đoàn viên tham gia đông hơn vì vậy từ ngày thứ hai mỗi ngày diện tích trồng tăng lên 4% so với ngày kế trước. Hỏi công việc sẽ hoàn thành vào ngày bao nhiêu? Biết rằng ngày 08/03 là ngày bắt đầu thực hiện và làm liên tục.

A. 25 / 03.

B. 26 / 03.

C. 23 / 03.

D. 24 / 03.

Câu 28. Cho các số thực dương x, y thóa mãn \({\log _{2{x^2} + xy + 3{y^2}}}(11x + 20y - 40) = 1\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(S = \frac{y}{x}\). Tính \(M + m\).

A. \(M + m = 2\sqrt {14} \).

B. \(M + m = \sqrt {10} \).

C. \(M + m = \frac{7}{2}\).

D. \(M + m = \frac{{11}}{6}\).

Câu 29. Tổng tất cá các nghiệm thực của phương trình \(15x{.5^x} = {5^{x + 1}} + 27x + 23\) bằng

A. 1 .

B. 0 .

C. 2 .

D. -1.

Câu 30. Đồ thị hàm số \(y = f(x)\) đối xứng với đồ thị của hàm số \(y = {a^x}(a > 0,a \ne 1)\) qua điểm \(I(1;1)\). Giá trị cua biểu thức \(f\left( {2 + {{\log }_a}\frac{1}{{2018}}} \right)\) bẳng:

A. -2016.

B. -2020.

C. 2016 .

D. 2020 .

Câu 31. Cho các số thực a, b thỏa mãn \(a > \frac{1}{3},b > 1\). Khi biểu thức \({\log _{3a}}b + {\log _b}\left( {{a^4} - 9{a^2} + 81} \right)\) đạt giá trị nhỏ nhất thì tổng a+b bẳng

A. \(9 + {2^{\sqrt 3 }}\).

B. \(3 + {9^{\sqrt 2 }}\).

C. \(3 + 3\sqrt 2 \).

D. \(2 + 9\sqrt 2 \).

Câu 32. Để đủ tiền mua nhà, anh An vay ngân hàng 500 triệu theo phương thức trả góp với lãi suất 0.85% một tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền cố định là 10 triệu đồng bao gồm cả tiền lãi vay và tiền gốc. Biết phương thức trả lãi và gốc không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao nhiêu tháng thì anh trả hết nợ ngân hàng? (tháng cuối có thể trả dưới 10 triệu đổng).

A. 67 .

B. 68 .

C. 66 .

D. 65 .

Câu 33. Một người vay ngân hàng 100 triệu đồng với lãi suất là 0.7%/ tháng theo thỏa thuận cứ cuối mỗi tháng người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết nợ (tháng cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng?

A. 21 .

B. 24 .

C. 22 .

D. 23 .

Câu 34. Cho\({\log _6}45 = a + \frac{{{{\log }_2}5 + b}}{{{{\log }_2}3 + c}}\), với \(a,b,c \in \mathbb{Z}\). Tính tổng a+b+c

A. 2 .

B. 1 .

C. - 4.

D. 0 .

Câu 35. Xét các số nguyên dương a, b sao cho phương trình \(a{\ln ^2}x + b\ln x + 5 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) và phương trình \(5{\log ^2}x + b\log x + a = 0\) có hai nghiệm phân biệt \({x_3},{x_4}\) thóa mãn \({x_1}{x_2} > {x_3}{x_4}\). Tìm giá trị nhó nhất của S=2a+3b

A. \({S_{\min }} = 33\).

B. \({S_{\min }} = 30\).

C. \({S_{\min }} = 17\).

D. \({S_{\min }} = 25\).

Câu 36. Bất phương trình \(\left( {{x^3} - 9x} \right)\ln (x + 5) \le 0\) có bao nhiêu nghiệm nguyên?

A. 4 .

B. 7 .

C. 6 .

D. Vô số.

Câu 37. Cho hàm số \(f(x) = {2^x} - {2^{ - x}}\). Gọi \({m_0}\) là số lớn nhất trong các số nguyên thõa mãn \(f(m) + f\left( {2m - {2^{12}}} \right) < 0\). Mệnh đề nào sau đây đúng?

A. \({m_0} \in [1513;2019)\).

B. \({m_0} \in [1009;1513)\).

C. \({m_0} \in [505;1009)\).

D. \({m_0} \in [1;505)\).

Câu 38. Tính tổng tất cả các nghiệm nguyên của bất phương trình \({\log _2}\left( {{x^2} + 3} \right) - {\log _2}x + {x^2} - 4x + 1 \le 0\).

A. 4 .

B. 6 .

C. 5 .

D. 3 .

Câu 39. Cho hàm số y=f(x) liên tục và đồng biến trên \(\left[ {0;\frac{\pi }{2}} \right]\), bất phương trình \(f(x) > \ln (\cos x) - {e^{\pi x}} + m\) (với m là tham số) thỏa mãn với mọi \(x \in \left( {0;\frac{\pi }{2}} \right)\) khi và chỉ khi:

A. \(m \le f(0) + 1\).

B. \(m > f(0) - 1\).

C. \(m < f(0) + 1\).

D. \(m \ge f(0) + 1\).

Câu 40. Ông An có 200 triệu đồng gửi ngân hàng với kì hạn 1 tháng với lãi suất 0.6%/ tháng được trả vào cuối kì. Sau mỗi kì hạn, ông đến tất toán cả lãi và gốc, rút ra 4 triệu đồng để tiêu dùng, số tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi suất không thay đổi trong suốt quá trình ông gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi, ông An tất toán và rút toàn bộ số tiền nói trên ớ ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đồng)

A. 169234 (nghìn đồng).

B. 165288 (nghìn đồng).

C. 169269 (nghìn đồng).

 D. 165269 (nghìn đồng).

Câu 41. Cho x, y thóa mãn \({\log _3}\frac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x(x - 9) + y(y - 9) + xy\). Tìm giá trị lớn nhất của \(P = \frac{{3x + 2y - 9}}{{x + y + 10}}\) khi x, y thay đổi.

A. 2 .

B. 3 .

C. 1 .

D. 0 .

Câu 42. Cho hai số thực a, b thỏa mãn a>0,0<b<2. Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{{{{(2b)}^a}}}{{{{\left( {{2^a} - {b^a}} \right)}^2}}} + \frac{{{2^a} + 2 \cdot {b^a}}}{{2 \cdot {b^a}}}\)

A. \({P_{\min }} = \frac{9}{4}\).

B. \({P_{\min }} = \frac{7}{4}\).

C. \({P_{\min }} = \frac{{13}}{4}\).

D. \({P_{\min }} = 4\).

Câu 43. Cho các số thực a, b>1 thỏa mãn điều kiện \({\log _2}a + {\log _3}b = 1\). Tìm giá trị lớn nhất của biểu thức \(P = \sqrt {{{\log }_3}a}  + \sqrt {{{\log }_2}b} \).

A. \(\sqrt {{{\log }_2}3 + {{\log }_3}2} \).

B. \(\sqrt {{{\log }_3}2}  + \sqrt {{{\log }_2}3} \)

C. \(\frac{1}{2}\left( {{{\log }_2}3 + {{\log }_3}2} \right)\).

D. \(\frac{2}{{\sqrt {{{\log }_2}3 + {{\log }_3}2} }}\).