Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài toán cực trị trong hình học không gian Toán lớp 12, tài liệu bao gồm 11 trang có phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Bài toán cực trị trong hình học không gian có đáp án gồm các nội dung chính sau:
A. Phương phương giải
- Gồm phương pháp giải Cực trị trong hình học không gian có đáp án.
B. Bài tập minh họa
- Gồm 16 bài tập có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài toán cực trị trong hình học không gian có đáp án.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BÀI TOÁN CỰC TRỊ HÌNH KHÔNG GIAN
A. PHƯƠNG PHÁP GIẢI
• Áp dụng các phương pháp tính thể tích thông qua tam giác vuông; các loại góc và khoảng cách trong không gian cũng như các công thức tính thể tích khối chóp, khối lăng trụ.
• Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa biến.
Cách 1. Áp dụng bất đẳng thức AM – GM cho các số thực dương
- Dạng 2 số: hoặc
- Dạng 3 số: hoặc
Cách 2. Khảo sát hàm số f(x) trên khoảng xác định (đạo hàm – lập bảng biến thiên)
B. BÀI TẬP MINH HỌA
|
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 4, cạnh bên SA vuông góc với mặt phẳng đáy (ABCD) và SC = 6. Tính thể tích lớn nhất của khối chóp đã cho A. B. C. D. |
Lời giải
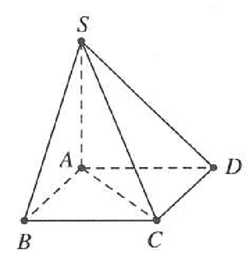
Đặt Diện tích hình chữ nhật ABCD là
Tam giác ABC vuông tại B, có
Tam giác SAC vuông tại A, có
Do đó, thể tích khối chóp S.ABCD là
Ta có
Dấu bằng xảy ra khi . Vậy . Chọn A
|
Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD = 4, các cạnh bên bằng nhau và bằng 6. Thể tích lớn nhất của khối chóp S.ABCD là A. B. C. D. |
Lời giải
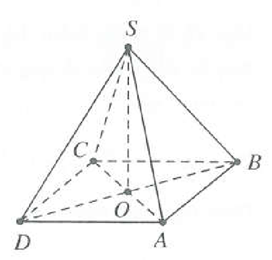
Vì Hình chiếu của S trên mặt phẳng (ABCD) là tâm đường tròn ngoại tiếp đáy
Đặt . Ta có
Tam giác SBO vuông tại O, có
Do đó, thể tích khối chóp S.ABCD là
Mà . Vậy . Chọn C
|
Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 4, SC = 6. Tam giác SAD cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích lớn nhất của khối chóp S.ABCD là A. B. C. D. |
Lời giải
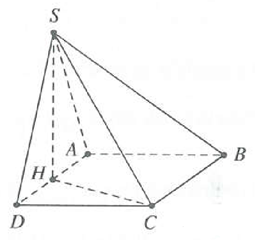
Gọi H là trung điểm AD. Tam giác SAD cân tại S
Ta có
Đặt
Tam giác HCD vuông tại D, có
Tam giác SHC vuông tại H, có
Do đó
Dấu bằng xảy ra khi . Vậy . Chọn D









