Bài tập Ôn tập chương IV đại số 9

Hoài Phạm Thị Thu Ngày: 08-03-2024 Lớp 9

Tải xuống 20 1.7 K 35

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Ôn tập chương IV đại số 9 , tài liệu bao gồm 20 trang, tuyển chọn 17 bài tập Ôn tập chương IV đại số 9 đầy đủ lý thuyết, phương pháp giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi Tuyển sinh lớp 10 môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Bài tập Ôn tập chương IV đại số 9 gồm các nội dung chính sau:

I. Kiến thức cần nhớ

- Tóm tắt lý thuyết ngắn gọn

II. Bài tập

- Gồm 17 bài tập vận dụng có lời giải chi tiết giúp học sinh tự rèn luyện cách giải các bài tập Ôn tập chương IV đại số 9

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BÀI ÔN TẬP CHƯƠNG IV ĐẠI SỐ LỚP 9

I. Kiến thức cần nhớ

1. Hàm số $y = {ax}^{2} (a \neq 0)$

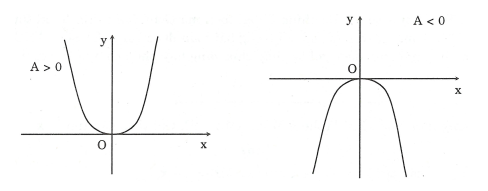
* Hàm số nghịch biến khi x < 0 đồng biến khi x >0

* y =0 là giá trị nhỏ nhất của hàm số đạt được khi x = 0

* Hàm số đồng biến khi x < 0 nghịch biến khi x > 0

* y =0 là giá trị lớn nhất của hàm số đạt được khi x =0

2. Phương trình bậc hai $x^{2} + bx + c = 0 (a \neq 0)$

$Δ = b^{2} - 4 a c$

$* ∆ > 0 phương trình có hai nghiệm phân biệt$

$x_{1} = \frac{- b + \sqrt{Δ}}{2 a}; x_{2} = \frac{- b - \sqrt{Δ}}{2 a}$

$* Nếu ∆ = 0 thì phương trình có nghiệm kép x_{1} = x_{2} = - \frac{b}{2 a}$

$* Nếu ∆ < 0 thì phương trình vô nghiệm$

$Δ' = b^{' 2} - a c (b = 2 b')$

$* Nếu ∆' > 0 thì phương trình có hai nghiệm .$

$x_{1} = \frac{- b^{'} + \sqrt{Δ^{'}}}{a}; x_{2} = \frac{- b^{'} - \sqrt{Δ^{'}}}{a}$

$* Nếu ∆' = thì phương trình có nghiệm kép : x_{1} = x_{2} = - \frac{b'}{a}$

$* Nếu ∆ < 0 thì phương trình vô nghiệm .$

Hệ thức Vi-ét và ứng dụng

Nếu $x_{1}, x_{2}$ là loại nghiệm của phương trình $x^{2} + bx + c = 0 (a \neq 0)$ thì:

$\{\begin{cases} \begin{matrix} S = x_{1} + x_{2} = - \frac{b}{a} \end{matrix} \\ P = x_{1} . x_{2} = \frac{c}{a} \end{cases}$

Muốn tìm hai số u và v, biết u+v = S, u.v=P và ta giải phương trình: $x^{2} - Sx + P = 0$

(Điều kiện để có u và v là $S^{2} - 4 P \geq 0$ )

Nếu a+b+c=0 thì phương trình $x^{2} + bx + c = 0 (a \neq 0)$ có hai nghiệm: $x_{1} = 1, x_{2} = \frac{c}{a}$
Nếu a-b+c=0 thì phương trình $x^{2} + bx + c = 0 (a \neq 0)$ có hai nghiệm: . $x_{1} = - 1, x_{2} = - \frac{c}{a}$