Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 4 Bài 7: Phương trình quy về phương trình bậc hai. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 4 Bài 7: Phương trình quy về phương trình bậc hai. Mời các bạn đón xem:
Bài tập Toán 9 Chương 4 Bài 7: Phương trình quy về phương trình bậc hai
A. Bài tập Phương trình quy về phương trình bậc hai
I. Bài tập trắc nghiệm
Câu 1: Phương trình x4 - 6x2 - 7 = 0 có bao nhiêu nghiệm
A. 0
B. 1
C. 2
D. 4
Đặt x2 = t (t ≥ 0) ta được phương trình t2 - 6t - 7 = 0 (*)
Nhận thấy a - b + c = 1 + 6 - 7 = 0 nên phương trình (*) có hai nghiệm
t1 = -1(L); t2 = 7(N)
Với t = 7 ta có x2 = 7 ⇔ x = ± √7
Vậy phương trình đã cho có hai nghiệm.
Chọn đáp án C.
Câu 2: Phương trình (x + 1)4 - 5(x + 1)2 - 84 = 0 có tổng các nghiệm là:
Chọn đáp án B.
Câu 3: Phương trình Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án có số nghiệm là:
A. 2
B. 1
C. 0
D. 3
Lời giải:
Suy ra phương trình đã cho vô nghiệm.
Chọn đáp án C.
Câu 4:Phương trình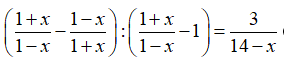 
có nghiệm là:
A. x = √2
B. x = 2
C. x = 3
D. x = 5
Lời giải:
Vậy phương trình có nghiệm là x = 5
Chọn đáp án D.
Câu 5: Tích các nghiệm của phương trình (x2 + 2x - 5)2 = (x2 - x + 5)2 là:
Chọn đáp án B.
Câu 6: Phương trình (x2 + x + 2)(x2 + x + 3) = 6 có bao nhiêu nghiệm?
A. 1
B.2
C. 3
D. 4
Chọn đáp án D.
Câu 7: Giải phương trình: (6x + 7)2(3x + 4)(x + 1) = 1
Vậy tập nghiệm của phương trình là .
Chọn đáp án B.
Câu 8: Phương trình 5x4 + 2x2 - 16 = 10 – x2 có bao nhiêu nghiệm?
A. 0
B. 2
C. 3
D. 4
Chọn đáp án B.
Câu 9: Phương trình: (2x2 + 12x + 10x).(2x + 4) = 0 có bao nhiêu nghiệm âm?
A. 1
B. 2
C. 3
D. 0
Chọn đáp án C.
Câu 10: Giải phương trình: 
Chọn đáp án B.
Câu 11: Số nghiệm của phương trình 3x3 + 3x2 + 5x + 5 = 0 là:
A. 2
B. 0
C. 1
D. 3
Vậy phương trình có nghiệm duy nhất x = −1
Đáp án cần chọn là: C
Câu 12: Nghiệm của phương trình x3 + 3x2 + x + 3 = 0 là:
A. x = ±1; x = −3
B. x = −1
C. x = 1
D. x = −3
Vậy phương trình có nghiệm duy nhất x = −3
Đáp án cần chọn là: D
Câu 13: Tổng các nghiệm của phương trình x(x + 1)(x + 2)(x + 3) = 8 là:
A. −3
B. 3
C. 1
D. −4
Ta có x(x + 1)(x + 2)(x + 3) = 8 ⇔ x (x + 3).(x + 1) (x + 2) = 8
⇔ (x2 + 3x)( x2 + 3x + 2) = 8
+) Với t = −3 ⇒ x2 + 3x + 1 = − 3 ⇔ x2 + 3x + 4 = 0, có ∆ = − 7 < 0 nên phương trình vô nghiệm.
Đáp án cần chọn là: A
Câu 14: Tổng các nghiệm của phương trình (x + 1)(x + 4)( x2 + 5x + 6) = 48 là:
Ta có (x + 1)(x + 4)( x2 + 5x + 6) = 48 ⇔ (x2 + 5x + 4) (x2 + 5x + 6) = 48
Đặt x2 + 5x + 5 = t, thu được phương trình:
+) Với t = −7 ⇒ x2 + 5x + 5 = − 7 ⇔ x2 + 5x + 12 = 0 có ∆ = − 23 < 0 nên phương trình vô nghiệm.
Đáp án cần chọn là: B
Câu 15: Hai nghiệm của phương trình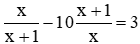 
là x1 > x2. Tính 3x1 + 4x2.
A. −3
B. 3
C. 7
D. −7
Điều kiện: x 0; x −1
Đặt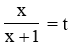 
(t ≥ 0), khi đó phương trình đã cho trở thành:
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
Câu 1: Giải phương trình
Lời giải:
Điều kiện x ≠ ±3.
Khi đó ta có
Ta có: Δ1 = (-4)2 - 4.3 = 16 - 12 = 4 > 0
Khi đó, phương trình (1) có hai nghiệm là:
Kết hợp điều kiện, vậy phương trình có hai nghiệm là x = 1
III. Bài tập vận dụng
Câu 1: Giải phương trình (x2 + 2x - 5)2 = (x2 - x + 5)2
Câu 2: Giải phương trình 
B. Lý thuyết Phương trình quy về phương trình bậc hai
1. Phương trình trùng phương
Phương trình trùng phương là phương trình có dạng ax4 + bx2 + c = 0 (a ≠ 0)
Giải phương trình ax4 + bx2 + c = 0 (a ≠ 0)
+ Đặt ẩn phụ x2 = t, t ≥ 0
+ Giải phương trình ẩn phụ mới: at2 + bt + c = 0
+ Với mỗi giá trị tìm được của t, lại giải phương trình x2 = t.
Ví dụ: Giải phương trình x4 - 13x2 + 36 = 0
Hướng dẫn:
Đặt x2 = t, t ≥ 0 Khi đó ta được phương trình bậc hai đối với ẩn t là t2 - 13t + 36 = 0 (*)
Ta có: Δt = (-13)2 - 4.36 = 169 - 144 = 25 > 0
Khi đó phương trình (*) có hai nghiệm là:
+ Với t1 = 9 ta có x2 = 9 có hai nghiệm là x1 = 3; x2 = -3.
+ Với t2 = 4 ta có x2 = 4 có hai nghiệm là x1 = 2; x2 = -2.
2. Phương trình chứa ẩn ở mẫu
Khi giải phương trình chứa ẩn ở mẫu thức, ta làm như sau:
+ Bước 1: Tìm điều kiện xác định của phương trình
+ Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức
+ Bước 3: Giải phương trình vừa nhận được
+ Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thỏa mãn điều kiện xác định, các giá trị thỏa mãn điều kiện xác định là nghiệm của phương trình đã cho.
Ví dụ: Giải phương trình
Hướng dẫn:
Điều kiện x ≠ ±3.
Khi đó ta có
Ta có: Δ1 = (-4)2 - 4.3 = 16 - 12 = 4 > 0
Khi đó, phương trình (1) có hai nghiệm là:
Kết hợp điều kiện, vậy phương trình có hai nghiệm là x = 1
3. Phương trình tích
Ta có: 
Để đưa phương trình đã cho về phương trình tích ta dùng phương pháp: đặt nhân tử chung, nhóm hạng tử, phương pháp thêm bớt hay sử dụng hằng đẳng thức đáng nhớ..
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack57. All Rights Reserved.
