Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Địa Lí lớp 10 Bài 4: Hàm số $y=a{x}^2$ (a ≠ 0) chọn lọc, có đáp án. Tài liệu có 7 trang gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Hàm số $y=a{x}^2$ (a ≠ 0) có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.

Giới thiệu về tài liệu:

- Số trang: 7 trang

- Số câu hỏi trắc nghiệm: 30 câu

- Lời giải & đáp án: có

Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Hàm số $y=a{x}^2$ (a ≠ 0) có đáp án - Toán lớp 9:

Hàm số $y=a{x}^2$ (a ≠ 0)

Câu 1: Cho hàm số y = ax² với a ≠ 0. Kết luận nào sau đây là đúng.

A. Hàm số nghịch biến khi a > 0 và x > 0

B. Hàm số nghịch biến khi a < 0 và x < 0

C. Hàm số nghịch biến khi a > 0 và x < 0

D. Hàm số nghịch biến khi a > 0 và x = 0

Lời giải:

Cho hàm số y = ax² (a ≠ 0)

a) Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0

b) Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0

Đáp án cần chọn là: C

Câu 2: Cho hàm số y = ax² với a ≠ 0. Kết luận nào sau đây là đúng.

A. Hàm số đồng biến khi a > 0 và x < 0

B. Hàm số đồng biến khi a > 0 và x > 0

C. Hàm số đồng biến khi a > 0 và x < 0

D. Hàm số đồng biến khi a < 0 và x = 0

Lời giải:

Cho hàm số y = ax² (a ≠ 0)

a) Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0

b) Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0

Đáp án cần chọn là: B

Câu 3: Kết luận nào sau đây là sai khi nó về đồ thị của hàm số y = ax² với a ≠ 0.

A. Đồ thị hàm số nhận trục tung làm trục đối xứng

B. Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị

C. Với a < 0 đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị

D. Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị

Lời giải:

Đồ thị của hàm số y = ax² (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy là trục đối xứng (O là đỉnh của parabol)

- Nếu Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị

- Nếu Với a < 0 đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị

Đáp án cần chọn là: B

Câu 4: Giá trị của hàm số y = f(x) = −7x² tại x₀ = −2 là:

A. 28          

B. 14          

C. 21          

D. −28

Lời giải:

Thay x₀ = −2 vào hàm số y = f(x) = −7x² ta được f(−2) = −7.(−2)² = −28

Đáp án cần chọn là: D

Câu 5: Giá trị của hàm số 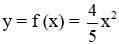 tại x₀ = − 5 là:

A. 20          

B. 10          

C. 4            

D. −20

Lời giải:

Thay x₀ = −5 vào hàm số 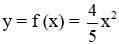 ta được:

Đáp án cần chọn là: A

Câu 6: Cho hàm số y = f(x) = (−2m + 1)x². Tìm giá trị của m để đồ thị đi qua điểm A (−2; 4)

A. m = 0     

B. m = 1     

C. m = 2     

D. m = −2

Lời giải:

Thay tọa độ điểm A (−2; 4) vào hàm số y = f(x) = (−2m + 1)x² ta được:

(−2m + 1).(−2)² = 4 ⇔ −2m + 1 = 1 ⇔ m = 0

Vậy m = 0 là giá trị cần tìm

Đáp án cần chọn là: A

Câu 7: Cho hàm số 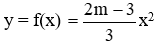. Tìm giá trị của m để đồ thị đi qua điểm B (−3; 5)

Lời giải:

Thay tọa độ điểm B (−3; 5) vào hàm số 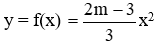 ta được:

Đáp án cần chọn là: C

Câu 8: Cho hàm số y = f(x) = −2x². Tổng các giá trị của a thỏa mãn f(a) = −8 + 4√3

A. 1            

B. 0            

C. 10          

D. −10

Lời giải:

Đáp án cần chọn là: B

Câu 9: Cho hàm số 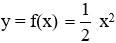. Tổng các giá trị của a thỏa mãn f(a) = 3 + √5

A. 1            

B. 2√5

C. 0            

D. −2

Lời giải:

Đáp án cần chọn là: C

Câu 10: Cho hàm số y = f(x) = 3x². Tìm b biết f(b) ≥ 6b + 9

Lời giải:

Đáp án cần chọn là: C

Câu 11: Cho hàm số y = f(x) = −2x². Tìm b biết f(b) ≤ −5b + 2

Lời giải:

Đáp án cần chọn là: D

Câu 12: Cho hàm số y = (2m + 2) x². Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x: y) là nghiệm của hệ phương trình: 

Lời giải:

Thay x = 2; y = 1 vào hàm số y = (2m + 2) x² ta được:

Đáp án cần chọn là: D

Câu 13: Cho hàm số y = (−3m + 1)x². Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x; y) là nghiệm của hệ phương trình 

Lời giải:

Thay x = 1; y = 2 vào hàm số y = (−3m + 1)x² ta được:

Đáp án cần chọn là: B

Câu 14: Cho hàm số y = (5m + 2)x² với 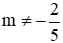. Tìm m để hàm số nghịch biến với mọi x > 0

Lời giải:

Để hàm số nghịch biến với mọi x > 0 thì a < 0 nên 5m + 2 < 0  ⇔  

Vậy 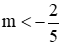 thỏa mãn điều kiện đề bài

Đáp án cần chọn là: A

Câu 15: Cho hàm số 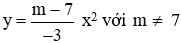. Tìm m để hàm số nghịch biến với mọi x < 0.

A. m > 7     

B. m < 7     

C. m < −7   

D. m > −7

Lời giải:

Để hàm số nghịch biến với mọi x < 0 thì a > 0 nên  

Vậy 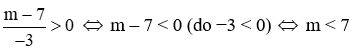 thỏa mãn điều kiện đề bài

Vậy m < 7 thỏa mãn điều kiện đề bài

Đáp án cần chọn là: B

Câu 16: Cho hàm số y = (4 – 3m)x² với 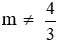. Tìm m để hàm số đồng biến với mọi x < 0

Lời giải:

Để hàm số đồng biến với mọi x > 0 thì a > 0 nên 4 – 3m > 0

Đáp án cần chọn là: C

Câu 17: Cho hàm số 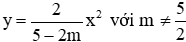. Tìm m để hàm số đồng biến với mọi x < 0

Lời giải:

Để hàm số đồng biến với mọi x < 0 thì a < 0 nên:

Đáp án cần chọn là: A