Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9: Hệ thức Vi ét (nâng cao) chọn lọc, có đáp án. Tài liệu có 10 trang gồm 14 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Hệ thức Vi ét (nâng cao) có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.
Giới thiệu về tài liệu:
- Số trang: 10 trang
- Số câu hỏi trắc nghiệm: 14 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Hệ thức Vi ét (nâng cao) có đáp án – Toán lớp 9:
Hệ thức Vi ét (nâng cao)
Câu 1: Cho phương trình x4 – mx3 + (m + 1)x2 – m(m + 1)x + (m + 1)2 = 0
Lời giải:
Khi m = −2, ta có phương trình x4 + 2x3 − x2 – 2x + 1 = 0
Kiểm tra ta thấy x = 0 không là nghiệm của phương trình
Chia hai vế của phương trình cho x2+ ta được:
Đặt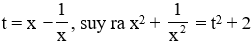 
. Thay vào phương trình nêu trên ta được:
t2 + 2t – 1 = 0 ⇔ t = −1
Đáp án cần chọn là: A
Câu 2: Có bao nhiêu giá trị của m để phương trình x2 – (2m + 1)x + m2 + 1 = 0 (1) có hai nghiệm phân biệt x1; x2 thỏa mãn (x1; x2)2 = x1
A. 2
B. 3
C. 4
D. 1
Lời giải:
Để phương trình đã cho có 2 nghiệm phân biệt thì
Vậy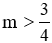 
thì phương trình có hai nghiệm phân biệt
Với 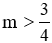thì phương trình có hai nghiệm phân biệt x1; x2
Vậy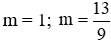 
thỏa mãn điều kiện bài toán
Đáp án cần chọn là: A
Câu 3: Cho phương trình x2 – (m – 1)x – m2 + m – 2 = 0, với m là tham số. Gọi hai nghiệm của phương trình đã cho là x1; x2. Tìm m để biểu thức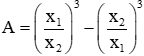 
đạt giá trị lớn nhất
A. m = 4
B. m = 3
C. m = 2
D. m = 1
Lời giải:
+) Xét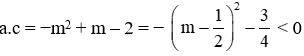 
với mọi m ∈ R
Vậy phương trình luôn có hai nghiệm trái dấu với mọi m
+) Gọi hai nghiệm của phương trình đã cho là x1; x2
Vì phương trình luôn có hai nghiệm trái dấu nên x1x2 ≠ 0, do đó A được xác định với mọi x1; x2
Do x1; x2 trái dấu nên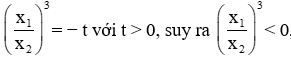 
, suy ra A < 0
Khi đó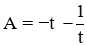 
mang giá trị âm và A đạt giá trị lớn nhất khi –A có giá trị nhỏ nhất.
Ta có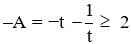 
(BĐT Cô-si), suy ra A ≤ −2. Đẳng thức xảy ra khi và chỉ khi 
Vậy với m = 1 thì biểu thức A đạt giá trị lớn nhất là −2
Đáp án cần chọn là: D
Câu 4: Cho phương trình 2x2 + 2mx + m2 – 2 = 0, với m là tham số. Gọi x1; x2 là hai nghiệm của phương trình. Tìm hệ thức liên hệ giữa x1; x2 không phụ thuộc vào m.
A. x1.x2 = x2 – x1 + 1
B. x1 − x2 = x2 – x1 – 1
C. x1.x2 = x2 – x1 + 1
D. x1.x2 = x1 + x2 − 1
Lời giải:
Ta có ∆ = m2 – 4(m – 1) = (m – 2)2 ≥ 0, với mọi m
Do đó phương trình luôn có nghiệm với mọi giá trị của m
Theo hệ thức Vi-ét, ta có x1 + x2 = m và x1.x2 = m – 1
Thay m = x1 + x2 vào x1.x2 = m – 1, ta được x1.x2 = x1 + x2 – 1
Vậy hệ thức liên hệ giữa x1; x2 không phụ thuộc vào m là x1.x2 = x1 + x2 – 1
Đáp án cần chọn là: D
Câu 5: Cho phương trình x2 – (2m + 1)x + 2m2 – 3m + 1 = 0, với m là tham số. Gọi x1; x2 là nghiệm của phương trình. Chọn câu đúng.
Lời giải:
Ta có ∆' =(m – 1)2 – (2m2 – 3m + 1) = −m2 + m = m(1 – m). Để phương trình có hai nghiệm 
Đáp án cần chọn là: A
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
