Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 1 Bài 4: Liên hệ giữa phép chia và phép khai phương. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 4: Liên hệ giữa phép chia và phép khai phương. Mời các bạn đón xem:
Bài tập Toán 9 Chương 1 Bài 4: Liên hệ giữa phép chia và phép khai phương
A. Bài tập Liên hệ giữa phép chia và phép khai phương
I. Bài tập trắc nghiệm
Câu 1: Giá trị của biểu thức 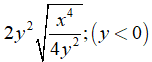
A. -xy2
B. xy2
C. -x2y
D. x2y
Ta có:
Chọn đáp án C.
Câu 2: Nghiệm của phương trình
Ta có:
Chọn đáp án D.
Câu 3: Giá trị của x trong phương trình
A. 10
B. 10 và -6
C. -6
D. -8
Ta có:
Chọn đáp án B.
Câu 4: Nghiệm của phương trình
A. 2
B. 3
C. 4
D. 5
Ta có:
Chọn đáp án C.
Câu 5: Không dùng máy tính, tính giá trị của biểu thức sau 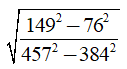
Ta có:
Chọn đáp án D.
Câu 6: Rút gọn biểu thức 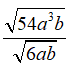
A. 9a
B.9a2
C.-3a
D. 3a
Ta có:
Chọn đáp án D.
Câu 7: Rút gọn biểu thức 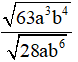
Ta có:
Chọn đáp án B.
Câu 8: Rút gọn biểu thức 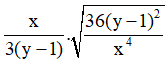
Ta có:
Chọn đáp án C.
Câu 9: Rút gọn biểu thức 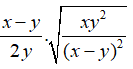
Ta có:
Chọn đáp án A.
Câu 10: Tính
Ta có:
Chọn đáp án B.
Câu 11: Với x, y ≥ 0; x ≠ y, rút gọn biểu thức 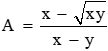
Đáp án cần chọn là: D
Câu 12: Với x, y ≥ 0; 3x ≠ y, rút gọn biểu thức 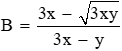
Đáp án cần chọn là: C
Câu 13: Giá trị của biểu thức 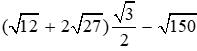
Đáp án cần chọn là: A
Câu 14: Giá trị của biểu thức 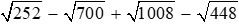
Đáp án cần chọn là: B
Câu 15: Với a ≥ 0, b ≥ 0, a ≠ b, rút gọn biểu thức 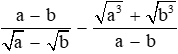
Đáp án cần chọn là: B
II. Bài tập tự luận có lời giải
Bài 1: Với nội dung quy tắc căn bậc hai, hãy tìm giá trị hợp lý của các biểu thức dưới đây:
a)
b)
c)
d)
Đáp án:
a) Giải :
b) 15 ;
c) 26 ;
d) 18
Bài 2: Yêu cầu tính giá trị của các công thức sau khi áp dụng quy tắc nhân:
a) ;
b) ;
c) ;
d) .
Đáp án:
a) Giải : = 3.5.4 = 60 ;
b) Đáp Số : 60 ;
c) Đáp Số : 24 ;
d) Đáp Số : 6
Bài 3: Áp dụng quy tắc khai phương để so sánh kết quả của từng cặp phép tính dưới đây?
a)
b)
c) ;
d)
Đáp án:
a) Đưa về so sánh hay so sánh với 10.
Kết quả được .
b) Tương tự câu a) :
So sánh với
hay so sánh với .
Do
Từ đó suy ra
c) Biến đổi
Do
Vậy .
d) So sánh hai bình phương là
Kết quả được
Bài 4: Dùng phương pháp tính nhẩm để so sánh các kết quả của hai biểu thức sau:
Đáp án:
Kết quả
Bài 5: Biểu diễn với điều kiện cho phép là a < 0 và b < 0 và áo dụng quy tắc nhân. Qua đó, tính giá trị
Đáp án:
Do
Khi đó, ta có
Áp dụng, ta có
7. Giá trị của bằng
III. Bài tập vận dụng
Câu 1: Rút gọn biểu thức sau:
Câu 2: Rút gọn biểu thức sau:
Câu 3: Giải phương trình
B. Lý thuyết Liên hệ giữa phép chia và phép khai phương
1. Căn bậc hai của một thương
Định lí. Với số a không âm và số b dương, ta có: .
Ví dụ 1. Tính:
a) ;
b) .
Lời giải:
a) ;
b) .
2. Quy tắc khai phương một thương
Muốn khai phương một thương , trong đó số a không âm và số b dương, ta có thể lần lượt khai phương của các số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.
Ví dụ 2. Áp dụng quy tắc khai phương một thương, hãy tính:
a) ;
b) .
Lời giải:
a) ;
b)
3. Quy tắc chia hai căn bậc hai
Muốn chia hai căn bậc hai của số a không âm và số b dương, ta có thể lấy số a chia cho số b rồi khai phương kết quả vừa tìm được.
(với a ≥ 0, b > 0).
Ví dụ 3. Tính:
a) ;
b) .
Lời giải:
a) .
b)
Chú ý. Một cách tổng quát, với biểu thức A không âm và biểu thức B dương, ta có: .
Ví dụ 4. Rút gọn biểu thức:
a) ;
b) với a > 0.
Lời giải:
a)
b) với a > 0.







