Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 1 Bài 6: Biến đổi đơn giản biểu thức chứa căn bậc hai. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 6: Biến đổi đơn giản biểu thức chứa căn bậc hai. Mời các bạn đón xem:
Bài tập Toán 9 Chương 1 Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
A. Bài tập Biến đổi đơn giản biểu thức chứa căn bậc hai
I. Bài tập trắc nghiệm
Câu 1: Kết quả của biểu thức rút gọn C = √125 - 3√45 + 2√20 ?
A. √5. B. 0. C. -√5. D. 2√5.
Đưa một thừa số ra ngoài dấu căn
Ta có:
Chọn đáp án B.
Câu 2: Kết quả so sánh nào sau đây đúng ?
Đưa thừa số vào trong dấu căn để sao sánh
Chọn đáp án A.
Chọn đáp án D.
Câu 6: Tính 
A. 1
B. 0
C.√2
D.2√2
Chọn đáp án B.
Câu 3: Tìm x biết: 
A. x = 2
B. x = 5
C. x = 10
D. x = 125
Chọn đáp án B.
Câu 4: So sánh hai số 5√3 và 4√5
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
Câu 1: Cho biểu thức
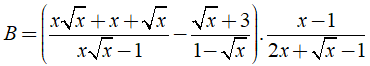(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
Tìm tất cả các giá trị của x để B < 0.
Ta có:
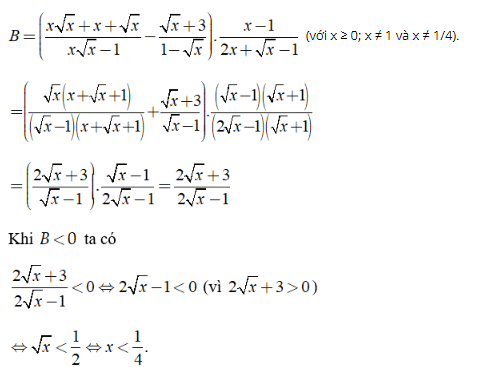
Kết hợp điều kiện ta có x ∈ [0; 1/4].
Câu 2: Giải các phương trình sau:
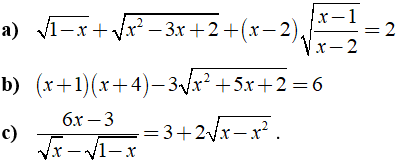
a) Điều kiện xác định:
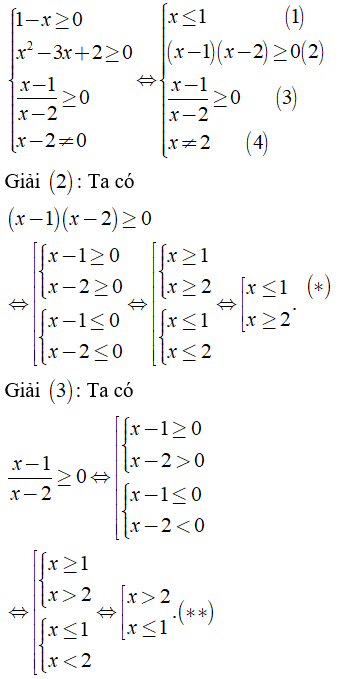
Kết hợp (1), (4), (*) và (**) ta có điều kiện xác định: x ≤ 1
Ta có
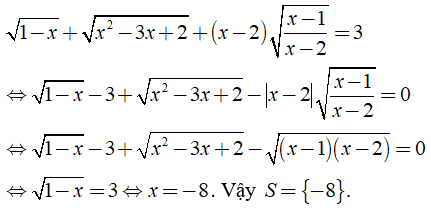
b) Điều kiện xác định: .
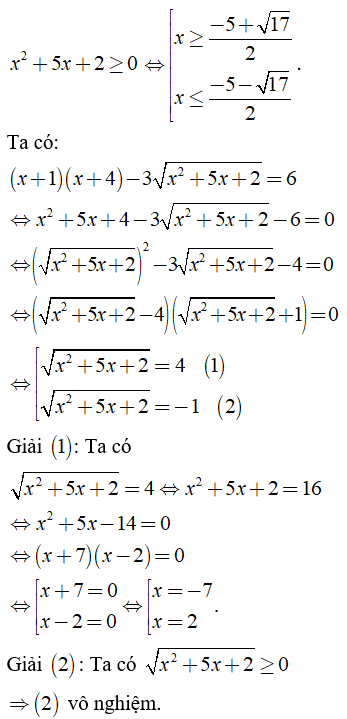
So sánh điều kiện ta có: x = -7; x = 2 (t/m). Vậy S = {-7; 2}.
c) Điều kiện xác định x ∈ [0; 1]\{1/2}.
Ta có:
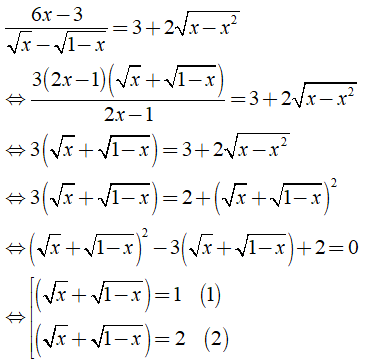
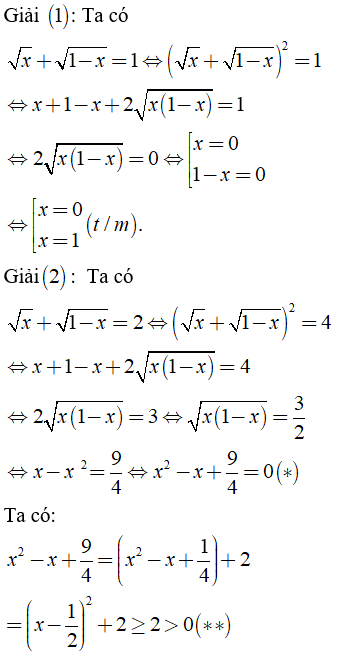
Từ (*) và (**) suy ra phương trình (2) vô nghiệm.
Vậy S = {0; 1}.
Câu 3: Rút gọn các biểu thức sau:
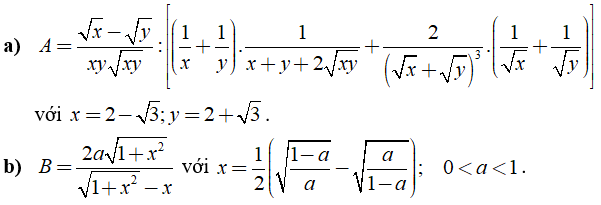
a) Ta có:
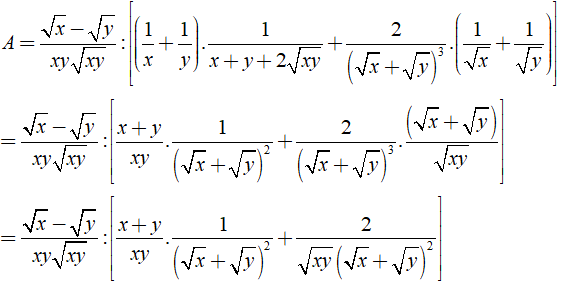
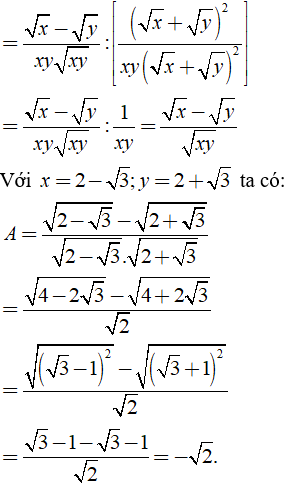
b) Ta có
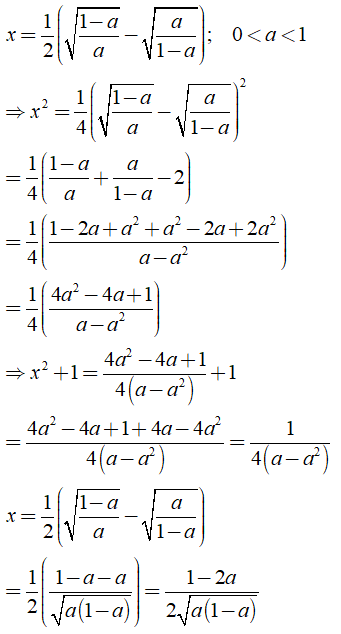
Khi đó: .
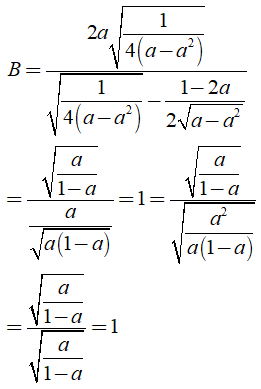
Câu 4: Chứng minh rằng
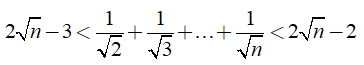(n ∈ N; n ≥ 2)
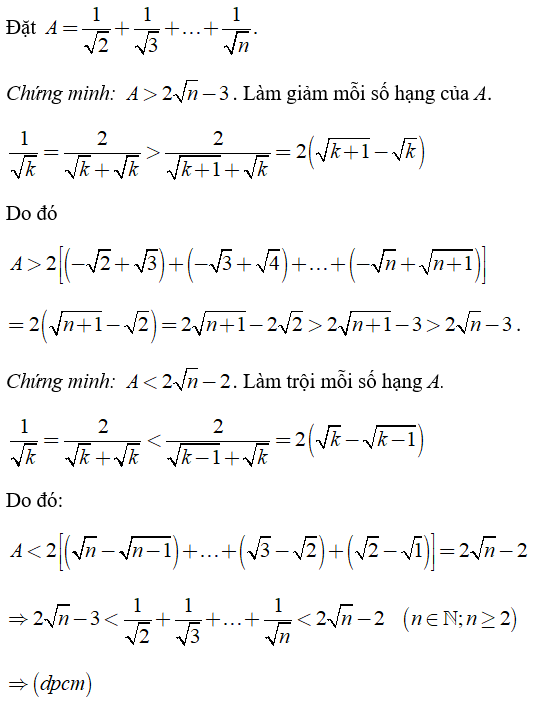
III. Bài tập vận dụng
Câu 1: Cho biểu thức
(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
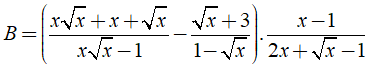
Tìm tất cả các giá trị của x để B < 0.
Câu 2: Giải các phương trình sau:
Câu 3: Rút gọn các biểu thức sau:
B. Lý thuyết Biến đổi đơn giản biểu thức chứa căn bậc hai
1. Đưa một thừa số ra ngoài dấu căn
• Với a ≥ 0, b ≥ 0, ta có: . Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.
• Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.
• Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.
Ví dụ 1.
a) ;
b)
Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có , tức là:
Nếu A ≥ 0 và B ≥ 0 thì ;
Nếu A < 0 và B ≥ 0 thì .
Ví dụ 2. Đưa thừa số ra ngoài căn:
a) với x ≥ 0, y < 0;
b) với x ≥ 0, y ≥ 0.
Lời giải:
a)
(với x ≥ 0, y < 0);
b)
(với x ≥ 0, y ≥ 0).
2. Đưa thừa số vào trong dấu căn
• Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.
Với A ≥ 0 và B ≥ 0 thì .
Với A < 0 và B ≥ 0 thì .
Ví dụ 2. Đưa thừa số vào trong căn:
a) ;
b) với a ≥ 0.
Lời giải:
a)
b)
với a ≥ 0.
• Có thể sử dụng phép đưa thừa số vào trong (hoặc ra ngoài) dấu căn để so sánh các căn bậc hai.
Ví dụ 3. So sánh và .
Lời giải:
Ta có: .
Vì nên .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
