Tailieumoi.vn xin giới thiệu chuyên đề Tính đơn điệu của hàm số thuộc chương trình Toán 12. Chuyên đề gồm 32 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 12.

Chuyên đề Tính đơn điệu của hàm số

Phần 1: Cách xét tính đơn điệu của hàm số cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

1. Định nghĩa: Cho hàm số y = f(x) xác định trên K, với K là một khoảng, nửa khoảng hoặc một đoạn.

    Hàm số y = f(x) đồng biến (tăng) trên K nếu ∀x₁, x₂ ∈ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).

    Hàm số y = f(x) nghịch biến (giảm) trên K nếu ∀x₁, x₂ ∈ K, x₁ < x₂ ⇒ f(x₁) > f(x₂).

2. Điều kiện cần để hàm số đơn điệu: Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.

    Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0,∀x ∈ K và f'(x) = 0 xảy ra tại một số điểm hữu hạn.

    Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0,∀x ∈ K và f'(x) = 0 xảy ra tại một số điểm hữu hạn.

3. Điều kiện đủ để hàm số đơn điệu: Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.

    Nếu f'(x) > 0,∀x ∈ K thì hàm số đồng biến trên khoảng K.

    Nếu f'(x) < 0,∀x ∈ K thì hàm số nghịch biến trên khoảng K.

    Nếu f'(x) = 0,∀x ∈ K thì hàm số không đổi trên khoảng K.

4. Các bước xét tính đơn điệu của một hàm số cho trước

   Bước 1: Tìm tập xác định của hàm số y = f(x)

   Bước 2: Tính đạo hàm f'(x) và tìm các điểm x_o sao cho f'(x_o) = 0 hoặc f'(x_o) không xác định.

   Bước 3: Lập bảng xét dấu và đưa ra kết luận

Ví dụ minh họa

Ví dụ 1: Xét tính đồng biến và nghịch biến của hàm số sau y=x³ - 6x² + 9x -3

Hướng dẫn

Tập xác định: D = R

Ta có y' = 3x² - 12x + 9

y' = 0 ⇔ 

Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng (-∞;1) và (3;+∞)

Hàm số nghịch biến trên khoảng (1;3)

Ví dụ 2: Xét tính đồng biến và nghịch biến của hàm số sau √(2x-x²)

Hướng dẫn

Tập xác định D = [0; 2]

Ta có : y' = 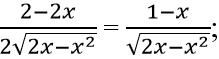 y' = 0 ⇔ x=1

Bảng biến thiên

Vậy hàm số đồng biến trên khoảng (0; 1); Hàm số nghịch biến trên khoảng (1; 2)

Ví dụ 3: Xét tính đồng biến và nghịch biến của hàm số sau y = (3x + 1)/(1 - x)

Hướng dẫn

Hàm số xác định và liên tục trên D = R\{1}.

Tìm y' = 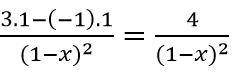 > 0; ∀x ≠ 1.

Bảng biến thiên:

Hàm số đã cho đồng biến trên các khoảng (-∞ ; 1)và (1 ; +∞).

Phần 2: Tìm tham số m để hàm số đơn điệu cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

1. Hàm đa thức bậc ba: y=f(x)=ax³+bx²+cx+d (a≠0)

⇒ f'(x)=3ax²+2bx+c

    Hàm đa thức bậc ba y=f(x) đồng biến trên R khi và chỉ khi 

   Hàm đa thức bậc ba y=f(x) nghịch biến trên R khi và chỉ khi

2. Hàm phân thức bậc nhất: 

    Hàm số đồng biến trên các khoảng xác định khi y'>0 hay ad-bc>0

   Hàm số nghịch biến trên các khoảng xác định khi y'>0 hay ad-bc<0

 

Ví dụ minh họa

Ví dụ 1: Cho hàm số 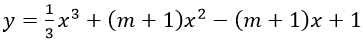 đồng biến trên tập xác định.

Hướng dẫn

      + Tập xác định: D=R

      + Ta có: y'=x²+2(m+1)x-(m+1)

      + Δ'=(m+1)²+4(m+1)=m²+6m+5

      + Để hàm số đồng biến trên tập xác định thì 

   Vậy giá trị của tham số cần tìm là -5≤m≤-1

Ví dụ 2: Cho hàm số 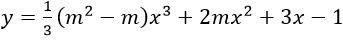. Tìm giá trị của m để hàm số luôn đồng biến trên R.

Hướng dẫn

      + Tập xác định: D=R

      + Đạo hàm y'≠(m²-m) x²+4mx+3

      + Hàm số luôn đồng biến trên R 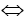 y'≥0 ∀ x∈R

    Xét m²-m=0 ⇒ 

   Với m=0 phương trình trở thành y=3x-1;y'=3>0 ∀x∈R

⇒ m=0 thỏa mãn yêu cầu bài toán.

    Với m=1 phương trình trở thành y=2x²+3x-1;y'=4x+3

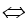
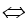
    Khi đó y'>0 4x+3>0 x<-3/4

⇒ m=1 không thỏa mãn yêu cầu bài toán.

    Xét m²-m≠0 

   Khi đó 

   Từ hai trường hợp trên ta có giá trị m cần tìm là -3≤m<0

Ví dụ 3: Cho hàm số 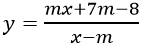. Tìm m để hàm số đồng biến trên từng khoảng xác định.

Hướng dẫn

      + Tập xác định: D=R\{m}

      + Đạo hàm 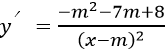 . Dấu của y' là dấu của biểu thức -m²-7m+8

      + Hàm số đồng biến trên từng khoảng xác định  y'>0 ∀x∈D

 -m²-7m+8>0  -8<m<1

    Vậy giá trị m cần tìm là -8<m<1

Phần 3: Phương pháp cô lập m trong khảo sát tính đơn điệu của hàm số cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

Bước 1: Tìm y'

Hàm số đồng biến trên khoảng K khi và chỉ khi y' ≥ 0 ∀ x ∈ K

Hàm số nghịch biến trên khoảng K khi và chỉ khi y' ≤ 0 ∀x ∈ K

Bước 2: Cô lập tham số m đưa về dạng m≥g(x) hoặc m ≤ g(x)

Bước 3: Vẽ bảng biến thiên của g(x)

Bước 4: Kết luận

m ≥ g(x) ∀ x ∈ K khi và chỉ khi m ≥ 

m ≤ g(x) ∀ x ∈ K khi và chỉ khi m ≤ 

Một số hàm số thường gặp

Hàm đa thức bậc ba: y = f(x) = ax³ + bx² + cx + d (a ≠ 0)

⇒ f'(x) = 3ax² + 2bx + c

Với a > 0 và f'(x) có hai nghiệm phân biệt x₁ < x₂

Hàm số đồng biến trên (α; β) khi và chỉ khi β ≤ xc hoặc α ≥ x₂

Hàm số nghịch biến trên (α; β) khi và chỉ khi x₁ ≤ α < β ≤ x₂

Với a <0 và f'(x) có hai nghiệm phân biệt x₁ < x₂

Hàm số đồng biến trên (α; β) khi và chỉ khi x₁ ≤ α < β ≤ x₂

Hàm số nghịch biến trên (α; β) khi và chỉ khi β≤x₁ hoặc α ≥ x₂

Hàm phân thức bậc nhất: y = (ax + b)/(cx + d) ⇒ y'= (ad - bc)/(cx + d)²

Hàm số đồng biến trên khoảng K khi và chỉ khi ad-bc>0 và -d/c ∉ K

Hàm số nghịch biến trên khoảng K khi và chỉ khi ad - bc < 0 và -d/c ∉ K

Ví dụ minh họa

Ví dụ 1: Tìm m để hàm số y = x³/3 - mx²+(1 - 2m)x- 1 đồng biến trên (1; +∞)

Hướng dẫn

TXĐ: D = R

Ta có y' = x² - 2mx + 1 - 2m

Hàm số đã cho đồng biến trên (1; +∞)⇔ ∀ x ∈(1; +∞),y' ≥ 0

⇔ ∀ x ∈ (1; +∞), x² -2mx + 1 - 2m ≥ 0 ⇔ ∀ x ∈(1; +∞), x² + 1 ≥ 2m(x + 1)

⇔ ∀ x ∈(1; +∞),2m ≤ (x² + 1)/(x + 1) (do x + 1 > 0 khi x > 1)

Xét hàm số f(x) = (x² + 1)/(x + 1), x ∈ (1; +∞)

f'(x) = (x² + 2x - 1)/(x + 1)² >0 với mọi x 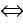 (1;+∞)

Ta có bảng biến thiên:

Dựa vào bảng biến thiên để 2m ≤ f(x),∀ x ∈(1; +∞) thì 2m ≤ 1 ⇔ m ≤ 1/2

Ví dụ 2: Tìm giá trị của tham số m để hàm số y = (2x - 1)/(x - m) nghịch biến trên khoảng (2; 3)

Hướng dẫn

TXĐ: D=R\{m}.

Ta có y'= (-2m + 1)/(x - m)² . Để hàm số nghịch biến trên khoảng (2; 3) thì hàm só phải xác định trên khoảng (2; 3) và y' < 0 ∀ x ∈ (2; 3).

Vậy giá trị của tham số m cần tìm là 

Ví dụ 3: Tìm các giá trị m để hàm số y = mx³ - x² + 3x + m - 2 đồng biến trên (-3 ; 0)

Hướng dẫn

TXĐ: D = R

Ta có y'= 3mx² - 2x + 3. Hàm số đồng biến trên khoảng (-3; 0) khi và chỉ khi:

y' ≥ 0,∀ x ∈(-3; 0) (Dấu '' = '' xảy ra tại hữu hạn điểm trên (-3; 0))

⇔ 3mx² - 2x + 3 ≥ 0, ∀ x ∈(-3; 0)

⇔ m ≥(2x-3)/(3x² ) = g(x) ∀ x ∈(-3;0)

Ta có: g'(x) = (-2x + 6)/(3x³ ); g'(x) = 0 ⇔ x = 3

Bảng biến thiên

Vậy m ≥ 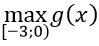= -1/3.

Phần 4: Tìm tham số m để hàm số đơn điệu trên đoạn có độ dài l cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

Tìm m để hàm số y = ax³ + bx² + cx + d có độ dài khoảng đồng biến (nghịch biến) = l.

   Bước 1: Tính y'=f'(x).

   Bước 2: Tìm điều kiện để hàm số có khoảng đồng biến và nghịch biến: 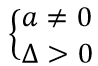 (1).

   Bước 3: Biến đổi |x₁-x₂ | = l thành (x₁+x₂ )² - 4x₁.x₂=l² (2).

   Bước 4: Sử dụng định lý Viét đưa (2) thành phương trình theo m.

   Bước 5: Giải phương trình, so với điều kiện (1) để chọn nghiệm.

Kiến thức cần nhớ

Hàm đa thức bậc ba: y = f(x) = ax³+bx²+ cx + d (a ≠ 0) ⇒ f'(x)=3ax²+ 2bx + c

Sử dụng định lý vi ét cho tam thức bậc hai f'(x)= 3ax² + 2bx + c có

Ví dụ minh họa

Ví dụ 1: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 1/3 x³ - 2mx² + 2mx - 3m + 4 nghịch biến trên một đoạn có độ dài là 3.

Hướng dẫn

Ta có f'(x) = x² - 4mx + 2m

Hàm số nghịch biến trên khoảng có độ dài bằng 3 khi và chỉ khi f'(x)= 0 có hai nghiệm phân biệt x₁,x₂ (x₁ < x₂) thỏa mãn |x₁-x₂ |=3

   + f'(x)= 0 có hai nghiệm phân biệt x₁,x₂ ⇔ Δ'= 4m² - 2m > 0 ⇔ 

Theo Vi ét ta có 

   + Với |x₁-x₂ | = 3 ⇔ (x₁ + x₁)² - 4x₁ x₂ - 9 = 0

 (thỏa mãn)

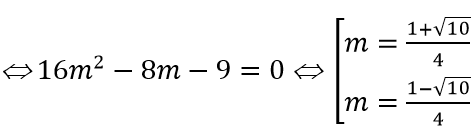
Vậy giá trị của m cần tìm là m=.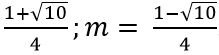

Ví dụ 2: Tìm m để hàm số y = -x³ + 3x² + (m-1)x + 2m - 3 đồng biến trên một khoảng có độ dài nhỏ hơn 1

Hướng dẫn

Ta có f'(x)= -3x² + 6x + m - 1

Hàm số đồng biến trên khoảng có độ dài lớn hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x₁,x₂ (x₁ < x₂) thỏa mãn |x₁-x₂ | > 1

   + f'(x)= 0 có hai nghiệm phân biệt x₁,x₂ ⇔ Δ'= 3m + 6 > 0 ⇔ m > -2

Theo Vi ét ta có 

   + Với |x₁-x₂ | > 1 ⇔ (x₁+x₂ )²-4x₁ x₂-1 > 0 ⇔ 4m + 5 > 0 ⇔ m > -5/4

Kết hợp điều kiện ta được m > -5/4

Ví dụ 3: Xác định m để hàm só y = -x⁴ +(m - 2) x² + 1 có khoảng nghịch biến (x₁;x₂) và độ dài khoảng này bằng 1.

Hướng dẫn

Ta có y' = -4x³ + 2(m - 2)x 

Để hàm số có khoảng nghịch biến (x₁;x₂) thì phương trình -2x² + m - 2 = 0 phải có hai nghiệm phân biệt 

Giả sử x₁ < 0 < x₂, khi đó hàm số sẽ nghịch biến trên khoảng (x₁;0) và (x₂; +∞)

Vì độ dài khoảng nghịch biến bằng 1 nên khoảng (x₁;0) có độ dài bằng 1 hay x₁ = -1

Vì -2x² + m - 2 = 0 có một nghiệm là -1 nên -2 + m - 2 = 0 ⇔ m = 4 (thỏa mãn)

Vậy giá trị của tham số m cần tìm là m = 4

Phần 5: Cách xét tính đơn điệu của hàm đa thức cực hay, có lời giải

A. Phương pháp giải

Bước 1: Tìm tập xác định D.

Bước 2: Tính đạo hàm y' = f'(x).

Bước 3: Giải phương trình f'(x) = 0.

Bước 4: Lập bảng biến thiên.

Bước 5: Kết luận.

B. Ví dụ minh họa

Ví dụ 1: Tìm khoảng đồng biến của hàm số y = -x³ + 6x² - 9x + 4

A. (0;3)

B. (1;3)

C. (-∞;0)

D. (2;+∞)

Lời giải

Chọn B

Bảng biến thiên:

Dựa vào bảng biến thiên, hàm số đồng biến trên khoảng (1;3).

Ví dụ 2: Cho hàm số: y = f(x) = x³ + 3x² + 3x + 2. Hãy chọn câu đúng:

A. Hàm số f(x) nghịch biến trên R

B. Hàm số f(x) đồng biến trên R

C. Hàm số f(x) không đổi trên R

D. Hàm số f(x) nghịch biến trên (-∞;-1)

Lời giải

Chọn B

Bảng biến thiên:

Ví dụ 3: Tìm khoảng đồng biến của hàm số: y = -x⁴ + 4x² - 3.

Lời giải

Chọn C

Bảng biến thiên:

Phần 6: Cách xét tính đơn điệu của hàm số lượng giác cực hay, có lời giải

A. Phương pháp giải

Bước 1: Tìm tập xác định D.

Bước 2: Tính đạo hàm y' = f'(x).

Bước 3: Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.

Bước 4: Lập bảng biến thiên.

Bước 5: Kết luận.

B. Ví dụ minh họa

Ví dụ 1: Tìm các khoảng đồng biến của hàm số: y = 2sin⁡x + cos⁡2x, x ∈ [0;π]

Lời giải

Chọn C

Bảng biến thiên

Ví dụ 2: Tìm các khoảng nghịch biến của hàm số: y = sin²⁡x + cos⁡x, x ∈ (0;π).

Lời giải

Chọn B

Bảng biến thiên

Ví dụ 3: Cho hàm số: y = f(x) = x - sin⁡x, x ∈ [0;π]. Hãy chọn câu đúng?

Lời giải

Chọn A

Bảng biến thiên

Phần 7: Cách xét tính đơn điệu của hàm phân thức cực hay, có lời giải

A. Phương pháp giải

Bước 1: Tìm tập xác định D.

Bước 2: Tính đạo hàm y' = f'(x).

Bước 3: Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.

Bước 4: Lập bảng biến thiên.

Bước 5: Kết luận.

B. Ví dụ minh họa

Ví dụ 1: Tìm khoảng đồng biến của hàm số: 

A. (0;+∞)

B. (-∞;2)

C. (-∞;1) và (1;+∞)

D. (-∞;+∞)

Lời giải

Chọn C

Bảng biến thiên:

Hàm số đã cho đồng biến trên các khoảng (-∞;1) và (1;+∞).

Ví dụ 2: Tìm khoảng nghịch biến của hàm số: .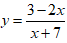

A. (-∞;7)

B. (-∞;+∞)

C. (-∞;-7) và (-7;+∞)

D. (-10;+∞)

Lời giải

Chọn C

Bảng biến thiên

Hàm số đã cho luôn nghịch biến trên: (-∞;-7) và (-7;+∞).

Ví dụ 3: Tìm khoảng nghịch biến của hàm số: 

A. (-∞;-5) và (1;+∞)

B. (-5;-2)

C. (-∞;-2) và (-2;+∞)

D. (-2;1)

Lời giải

Chọn A

Bảng biến thiên

Dựa vào bảng biến thiên, hàm số nghịch biến trên các khoảng (-∞;-5) và (1;+∞)

Xem thêm