Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 50 bài tập trắc nghiệm cực trị hàm hợp, tài liệu bao gồm 64 trang, 50 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

50 bài tập trắc nghiệm cực trị hàm hợp có đáp án và lời giải chi tiết

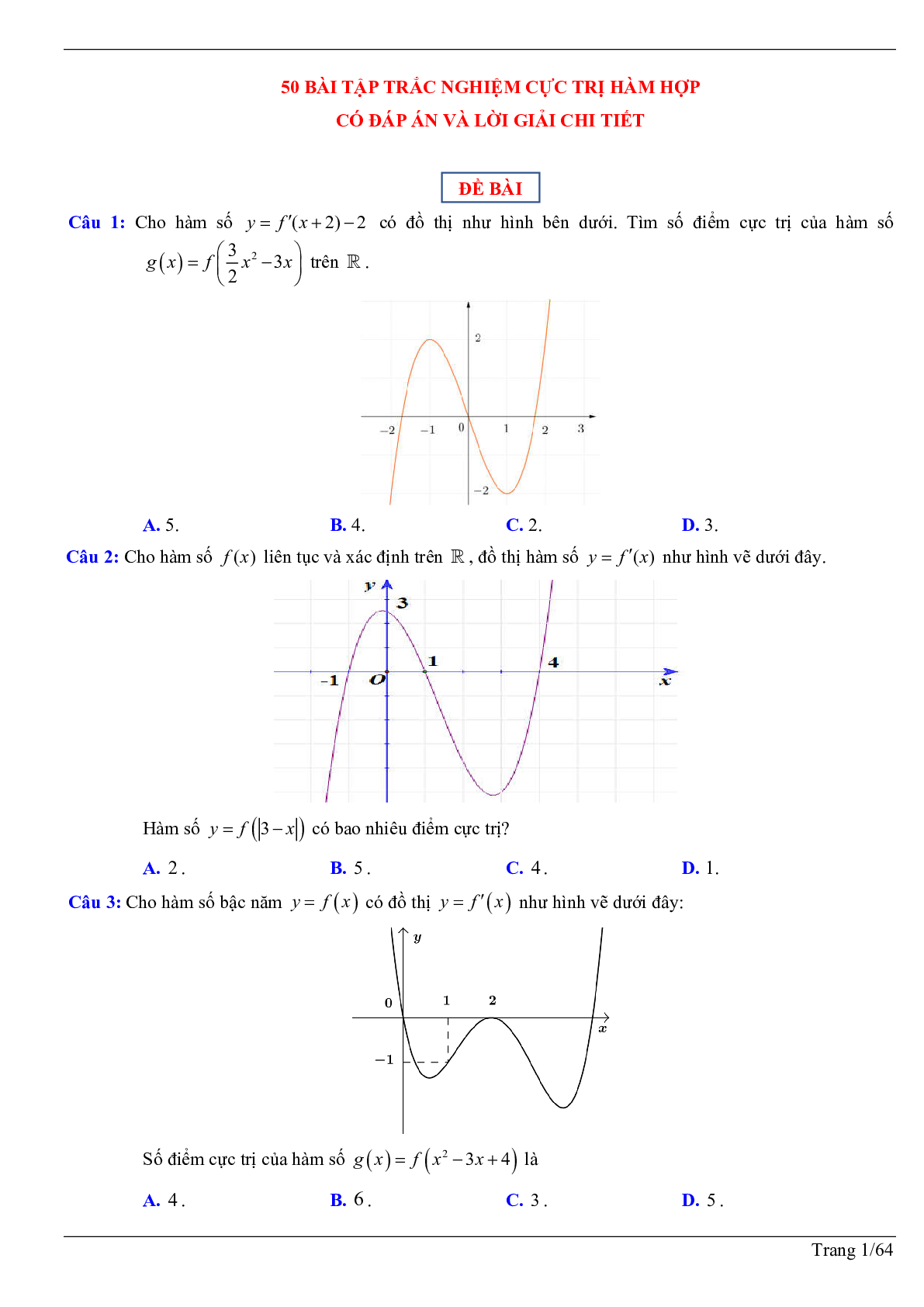
Câu 1: Cho hàm số \[y = f'(x + 2) - 2\] có đồ thị như hình bên dưới. Tìm số điểm cực trị của hàm số \[g(x) = f\left( {\frac{3}{2}{x^2} - 3x} \right)\] trên R.

A. 5.

B. 4.

C. 2.

D. 3.

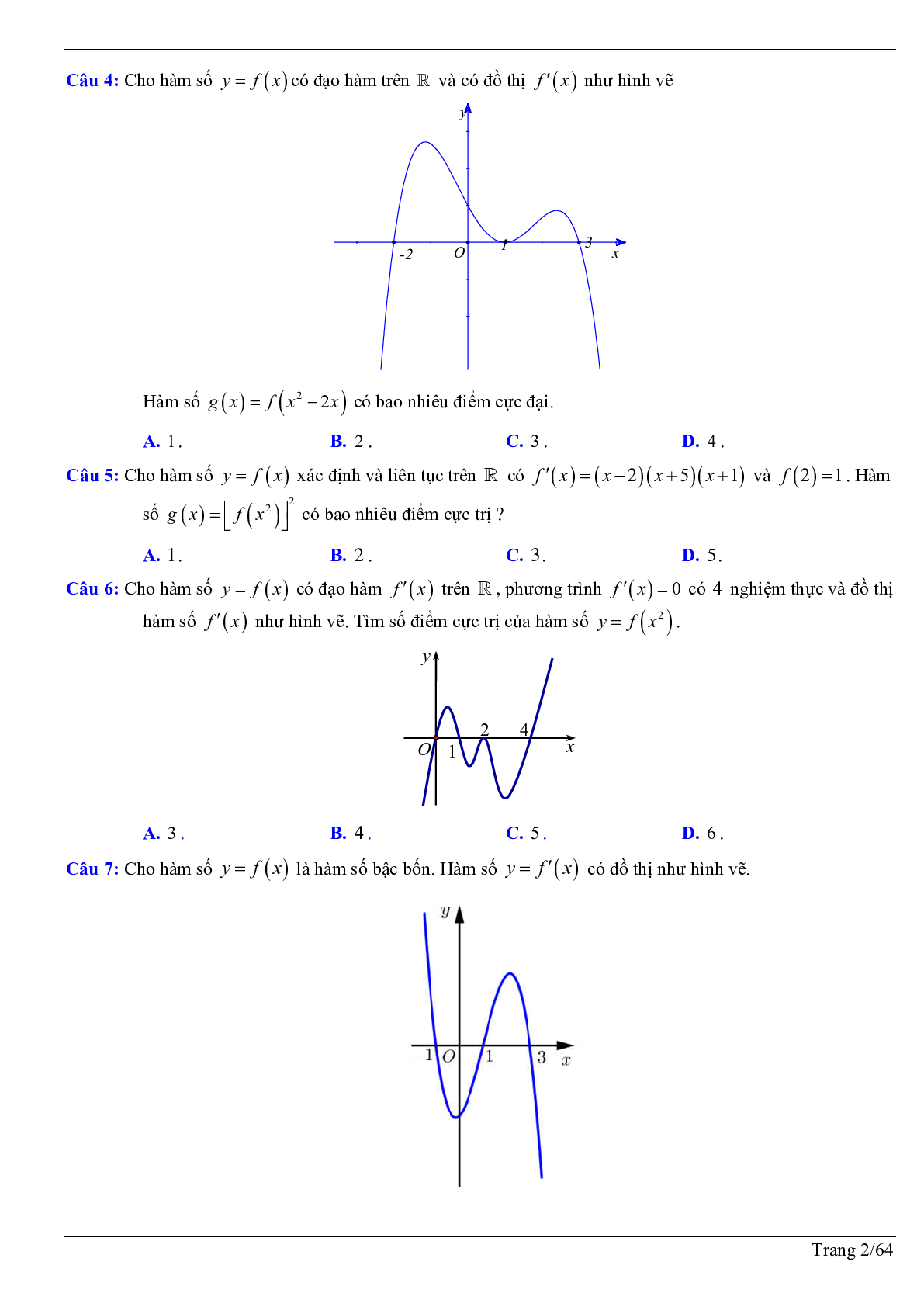
Câu 2: Cho hàm số \[f(x)\] liên tục và xác định trên R, đồ thị hàm số \[y = f'(x)\] như hình vẽ dưới đây.

Hàm số \[y = f\left( {\left| {3 - x} \right|} \right)\] có bao nhiêu điểm cực trị?

A. 2 .

B. 5 .

C. 4 .

D. 1.

Câu 3: Cho hàm số bậc năm \[y = f(x)\] có đồ thị \[y = f'(x)\] như hình vẽ dưới đây:

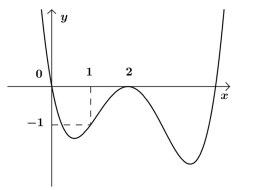
Số điểm cực trị của hàm số \[g(x) = f\left( {{x^2} - 3x + 4} \right)\] là

A. 4 .

B. 6 .

C. 3 .

D. 5 .

Câu 4: Cho hàm số \[y = f(x)\] có đạo hàm trên R và có đồ thị \[f'(x)\] như hình vẽ

Hàm số \[g(x) = f\left( {{x^2} - 2x} \right)\] có bao nhiêu điểm cực đại.

A. 1 .

B. 2 .

C. 3 .

D. 4 .

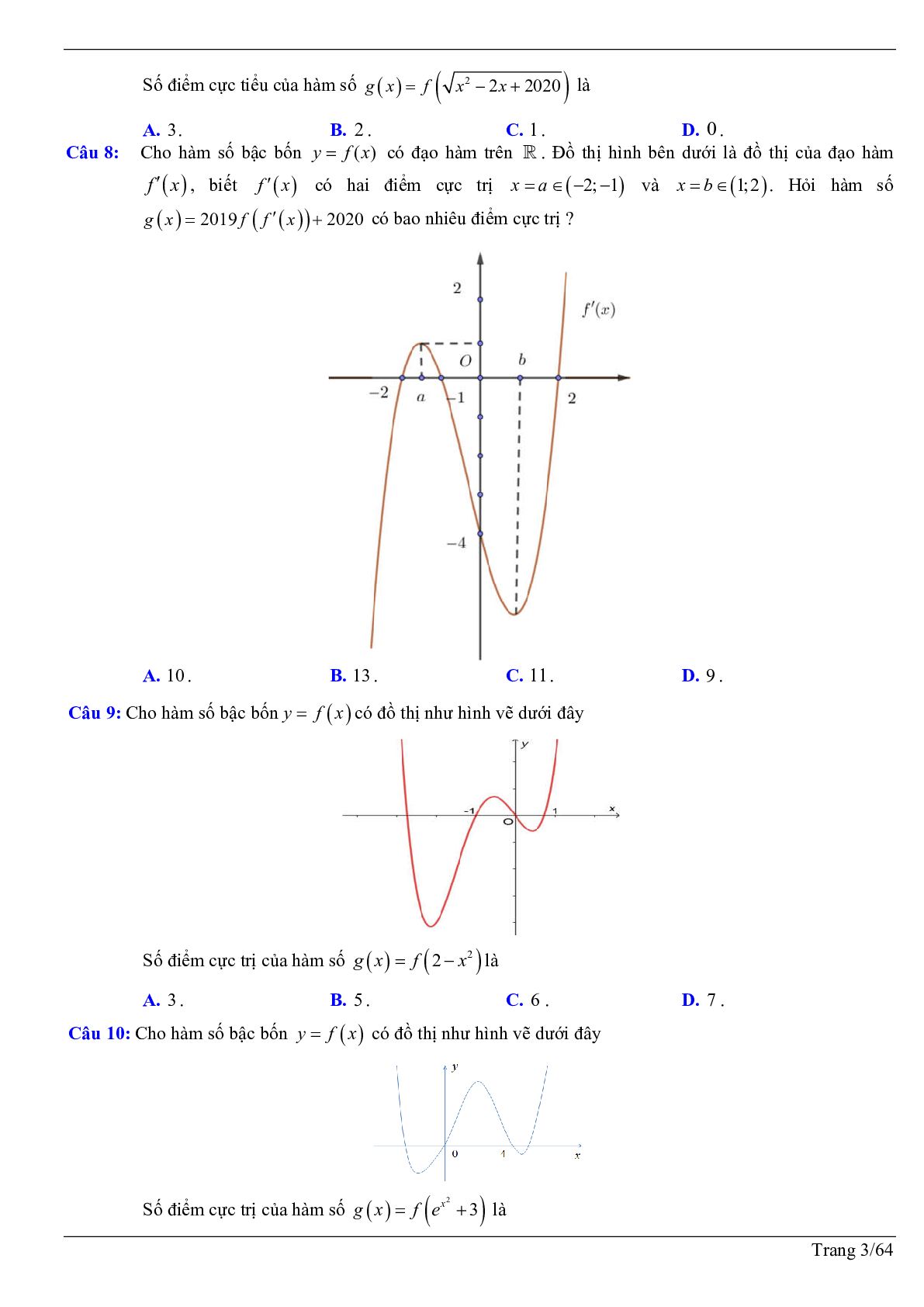
Câu 5: Cho hàm số \[y = f(x)\] xác định và liên tục trên R có \[f'(x) = (x - 2)(x + 5)(x + 1)\]và \[f(2) = 1\]. Hàm số \[g(x) = {\left[ {f({x^2})} \right]^2}\] có bao nhiêu điểm cực trị ?

A. 1.

B. 2 .

C. 3.

D. 5.

Câu 6: Cho hàm số \[y = f(x)\] có đạo hàm \[f'(x)\] trên R, phương trình \[f'(x) = 0\] có 4 nghiệm thực và đồ thị hàm số \[f'(x)\] như hình vẽ. Tìm số điểm cực trị của hàm số \[f({x^2})\].

A. 3 .

B. 4 .

C. 5 .

D. 6 .

Câu 7: Cho hàm số \[y = f(x)\] là hàm số bậc bốn. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ.

Số điểm cực tiểu của hàm số \[g(x) = f\left( {\sqrt {{x^2} - 2x + 2020} } \right)\] là

A. 3.

B. 2 .

C. 1.

D. 0 .

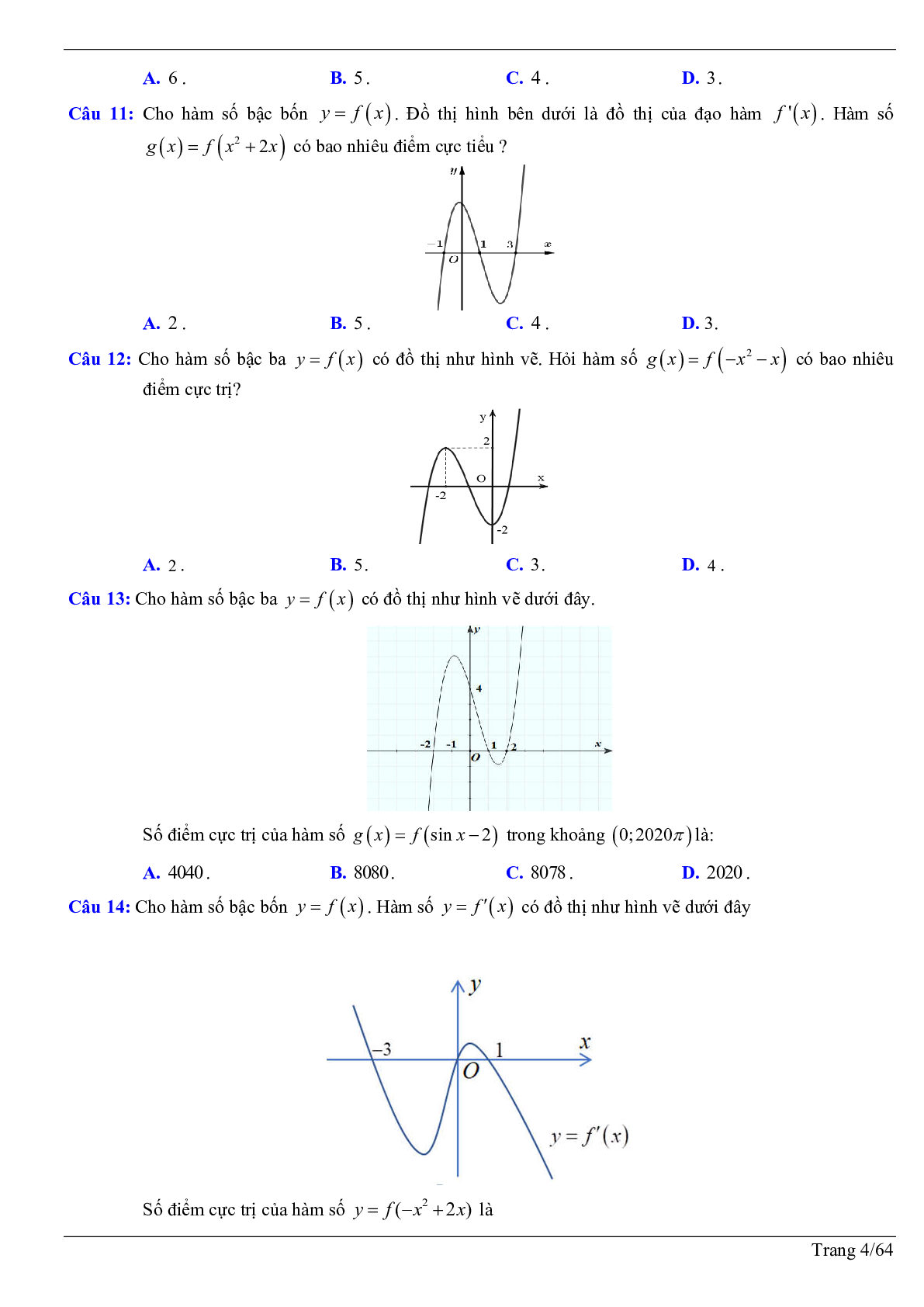
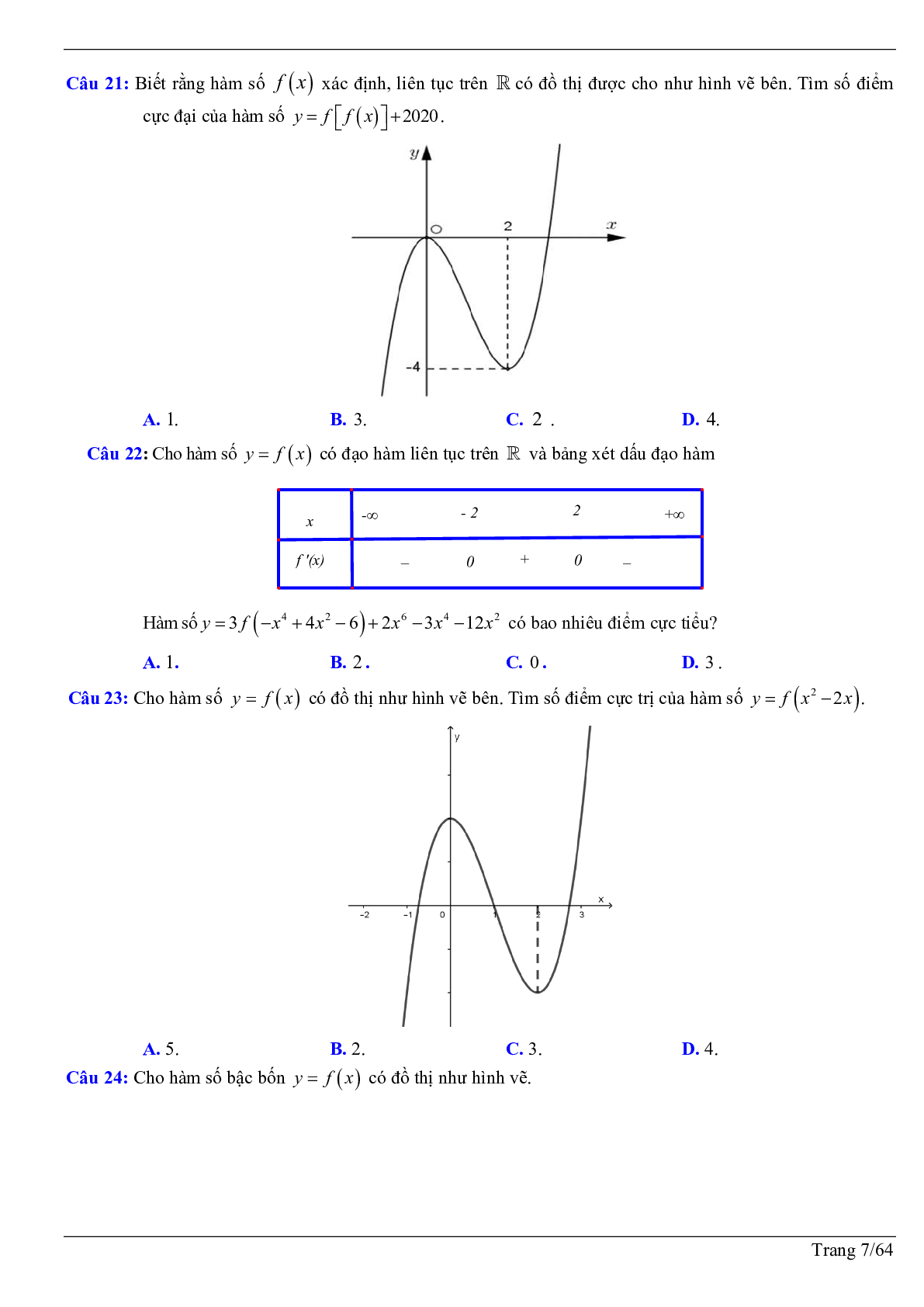
Câu 8: Cho hàm số bậc bốn \[y = f(x)\] có đạo hàm trên R. Đồ thị hình bên dưới là đồ thị của đạo hàm \[f'(x)\], biết \[f'(x)\] có hai điểm cực trị x = a Î (-2; -1) và x = b Î (1;2). Hỏi hàm số \[g(x) = 2019f\left( {f'(x)} \right) + 2020\] có bao nhiêu điểm cực trị ?

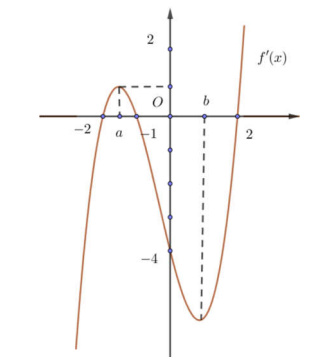
A. 10 .

B. 13 .

C. 11.

D. 9 .

Câu 9: Cho hàm số bậc bốn \[y = f(x)\] có đồ thị như hình vẽ dưới đây

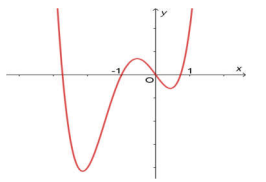
Số điểm cực trị của hàm số \[g(x) = f\left( {2 - {x^2}} \right)\] là

A. 3.

B. 5.

C. 6 .

D. 7 .

Câu 10: Cho hàm số bậc bốn \[y = f(x)\] có đồ thị như hình vẽ dưới đây

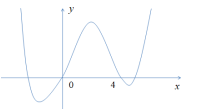
Số điểm cực trị của hàm số \[g(x) = f\left( {{e^{{x^2}}} + 3} \right)\] là

A. 6 .

B. 5.

C. 4 .

D. 3.

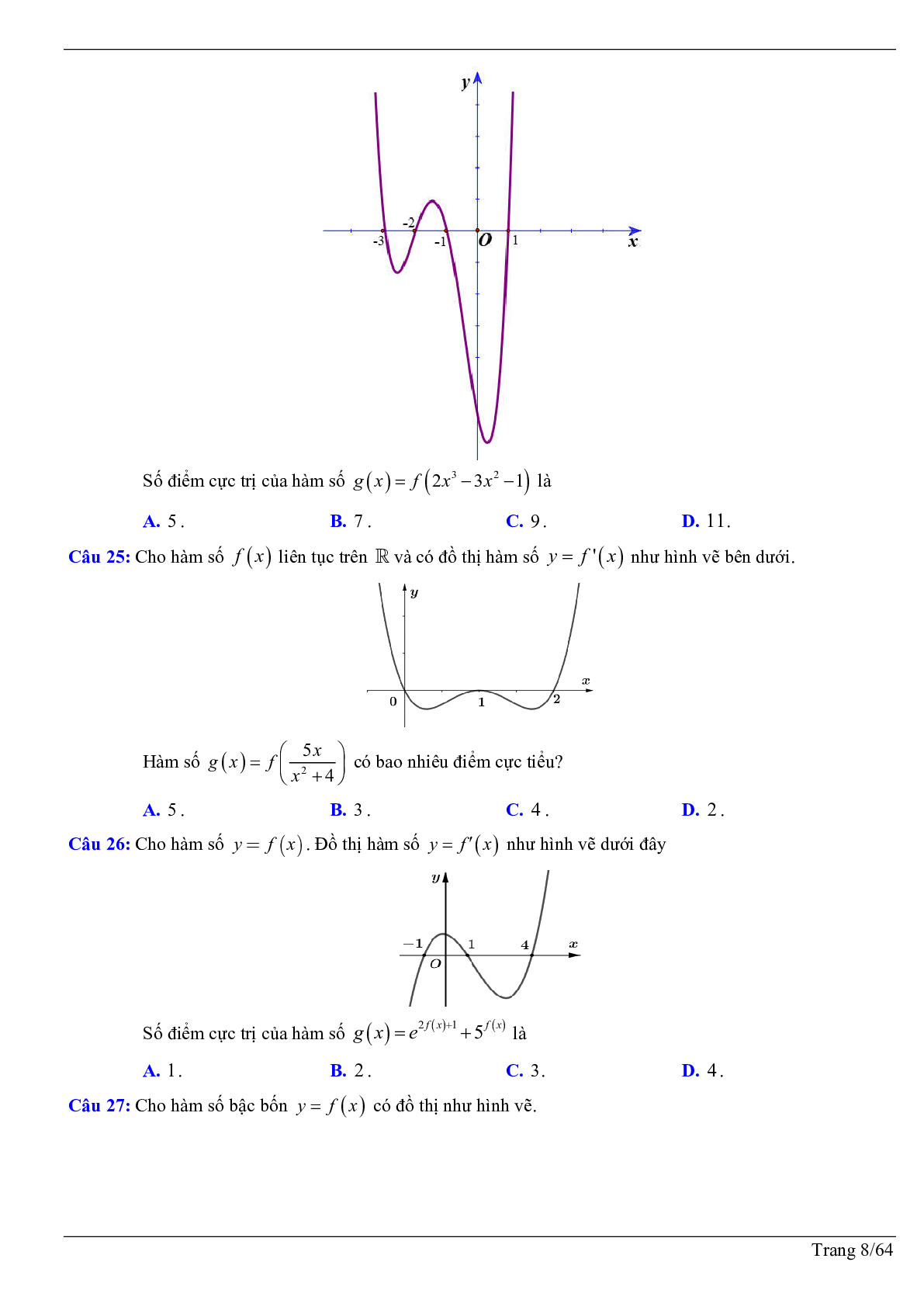
Câu 11: Cho hàm số bậc bốn \[y = f(x)\]. Đồ thị hình bên dưới là đồ thị của đạo hàm \[f'(x)\]. Hàm số \[g(x) = f\left( {{x^2} + 2x} \right)\] có bao nhiêu điểm cực tiểu ?

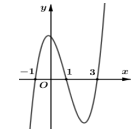
A. 2 .

B. 5 .

C. 4 .

D. 3.

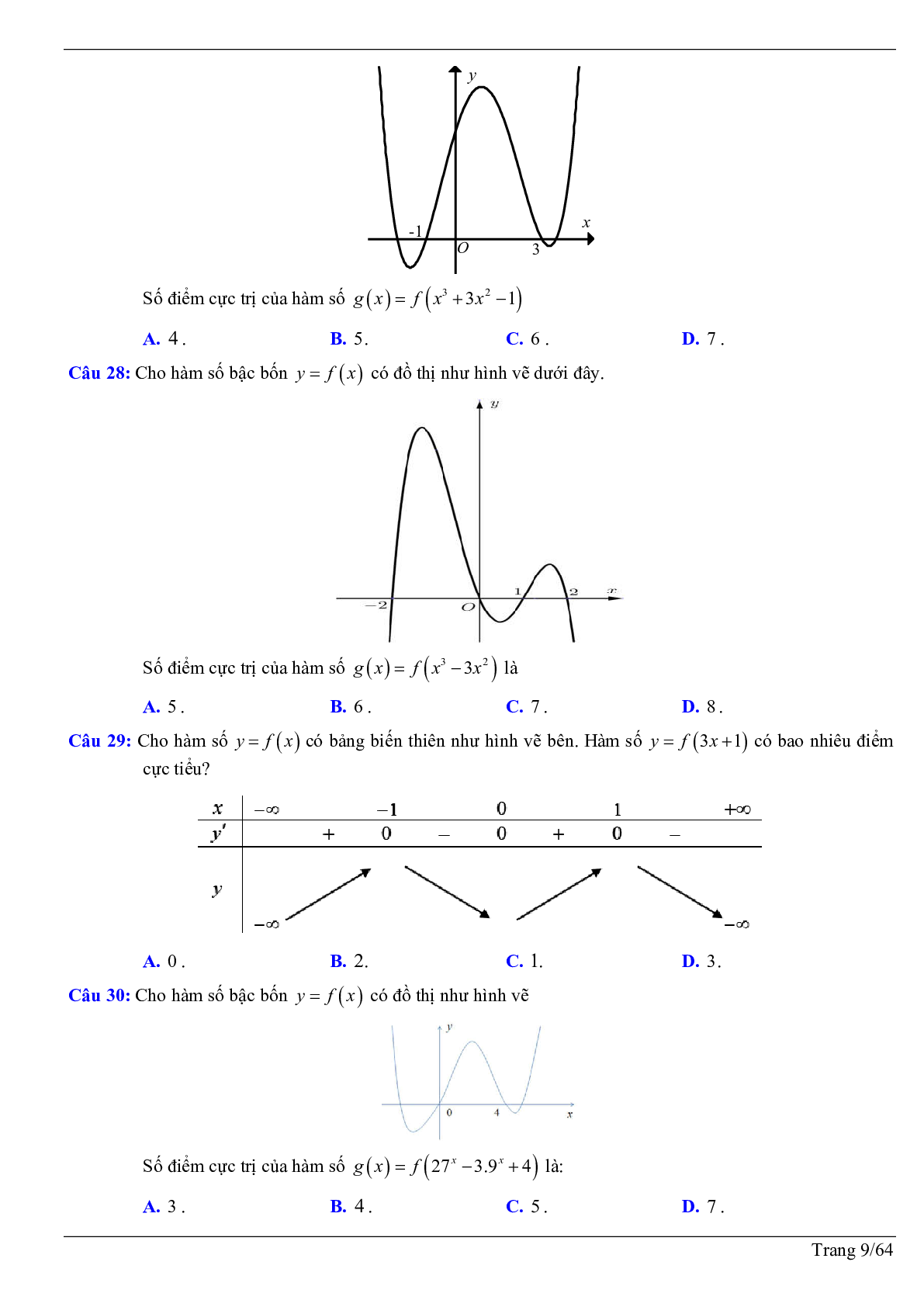
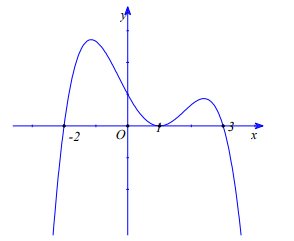
Câu 12: Cho hàm số bậc ba \[y = f(x)\] có đồ thị như hình vẽ. Hỏi hàm số \[g(x) = f\left( { - {x^2} - x} \right)\] có bao nhiêu điểm cực trị?

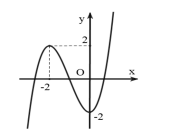
A. 2 .

B. 5.

C. 3.

D. 4 .

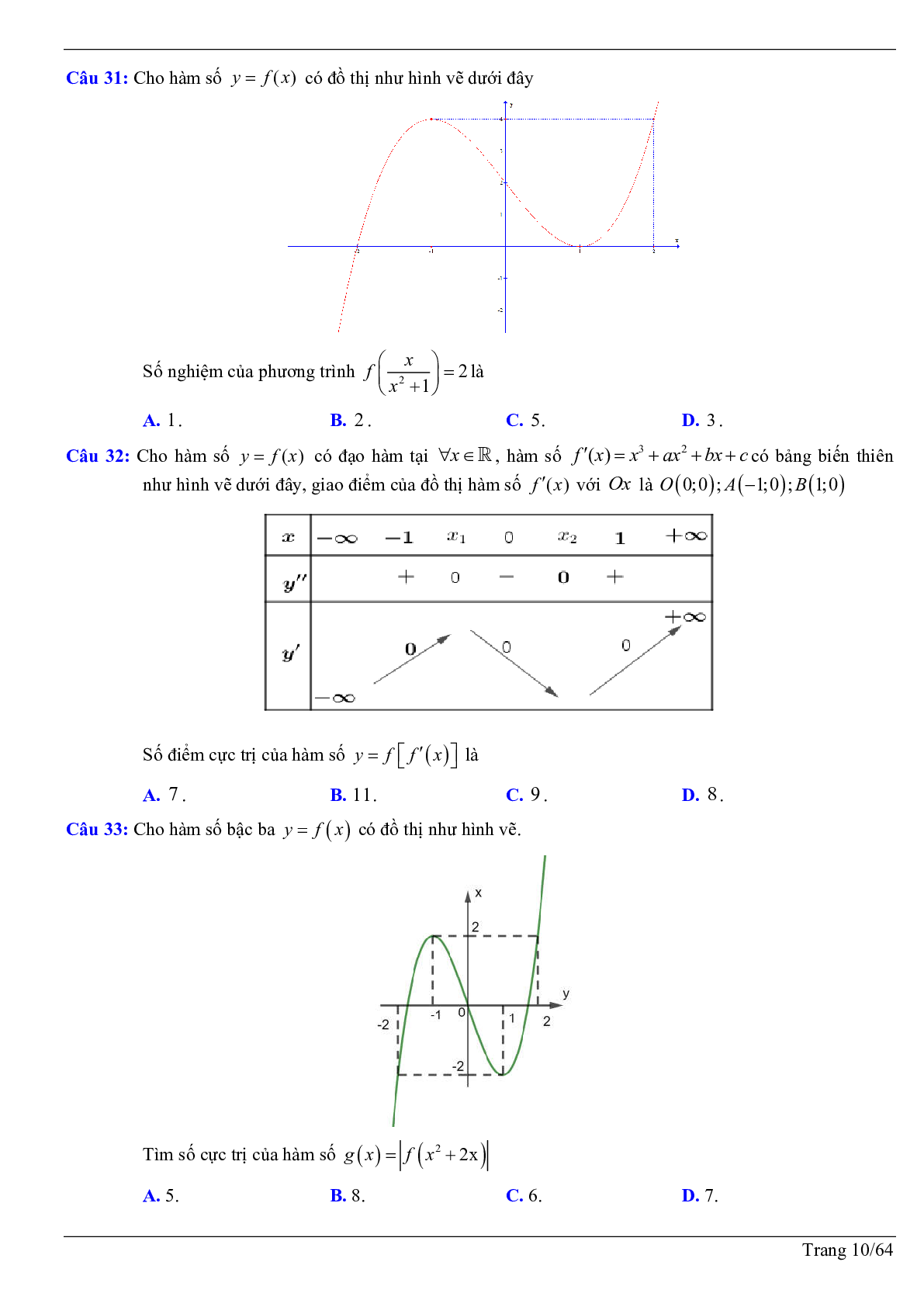
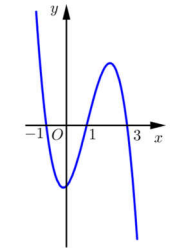
Câu 13: Cho hàm số bậc ba \[y = f(x)\] có đồ thị như hình vẽ dưới đây.

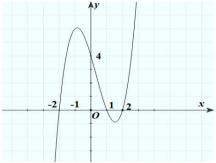
Số điểm cực trị của hàm số \[g(x) = f\left( {\sin x - 2} \right)\] trong khoảng (0;2020p) là:

A. 4040.

B. 8080.

C. 8078.

D. 2020.

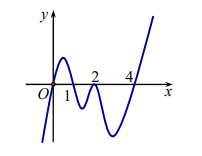
Câu 14: Cho hàm số bậc bốn \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ dưới đây

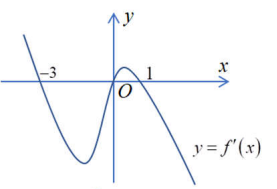
Số điểm cực trị của hàm số \[y = f\left( {{x^2} + 2x} \right)\] là

A. 4.

B. 2.

C. 3.

D. 5.

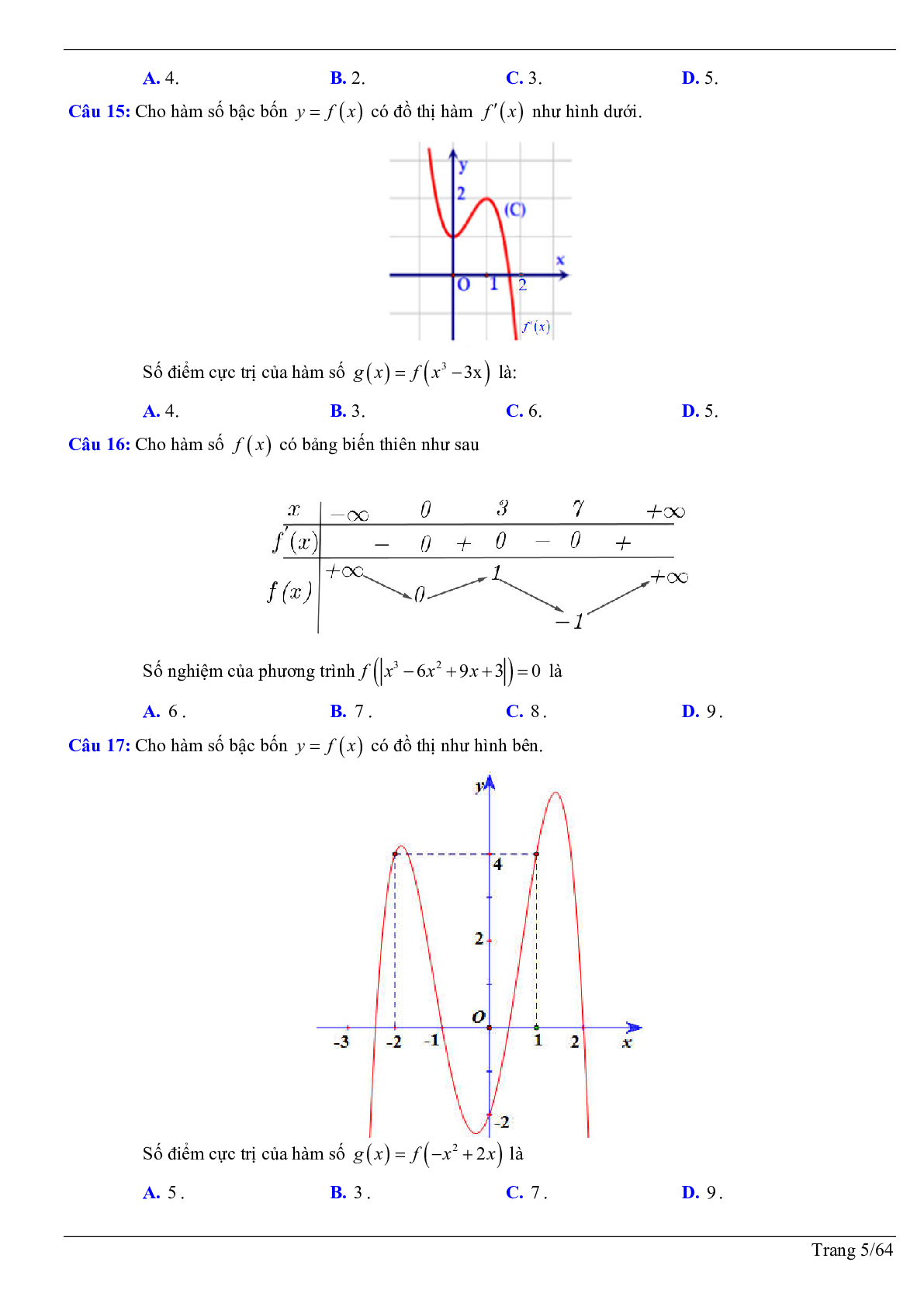
Câu 15: Cho hàm số bậc bốn \[y = f(x)\] có đồ thị hàm \[f'(x)\] như hình dưới.

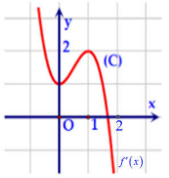
Số điểm cực trị của hàm số \[g(x) = f\left( {{x^3} - 3x} \right)\] là:

A. 4.

B. 3.

C. 6.

D. 5.

Câu 16: Cho hàm số \[f(x)\] có bảng biến thiên như sau

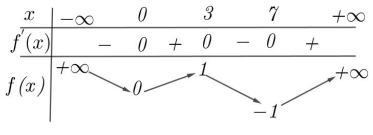
Số nghiệm của phương trình \[f\left( {\left| {{x^3} - 6{x^2} + 9x + 3} \right|} \right) = 0\] là

A. 6 .

B. 7 .

C. 8 .

D. 9 .

Câu 17: Cho hàm số bậc bốn \[y = f(x)\] có đồ thị như hình bên.

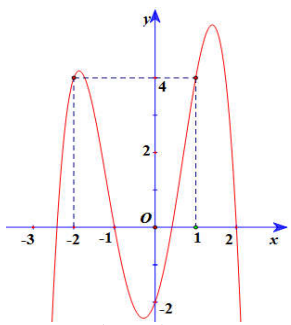
Số điểm cực trị của hàm số \[g(x) = f\left( { - {x^2} + 2x} \right)\] là

A. 5 .

B. 3 .

C. 7 .

D. 9 .

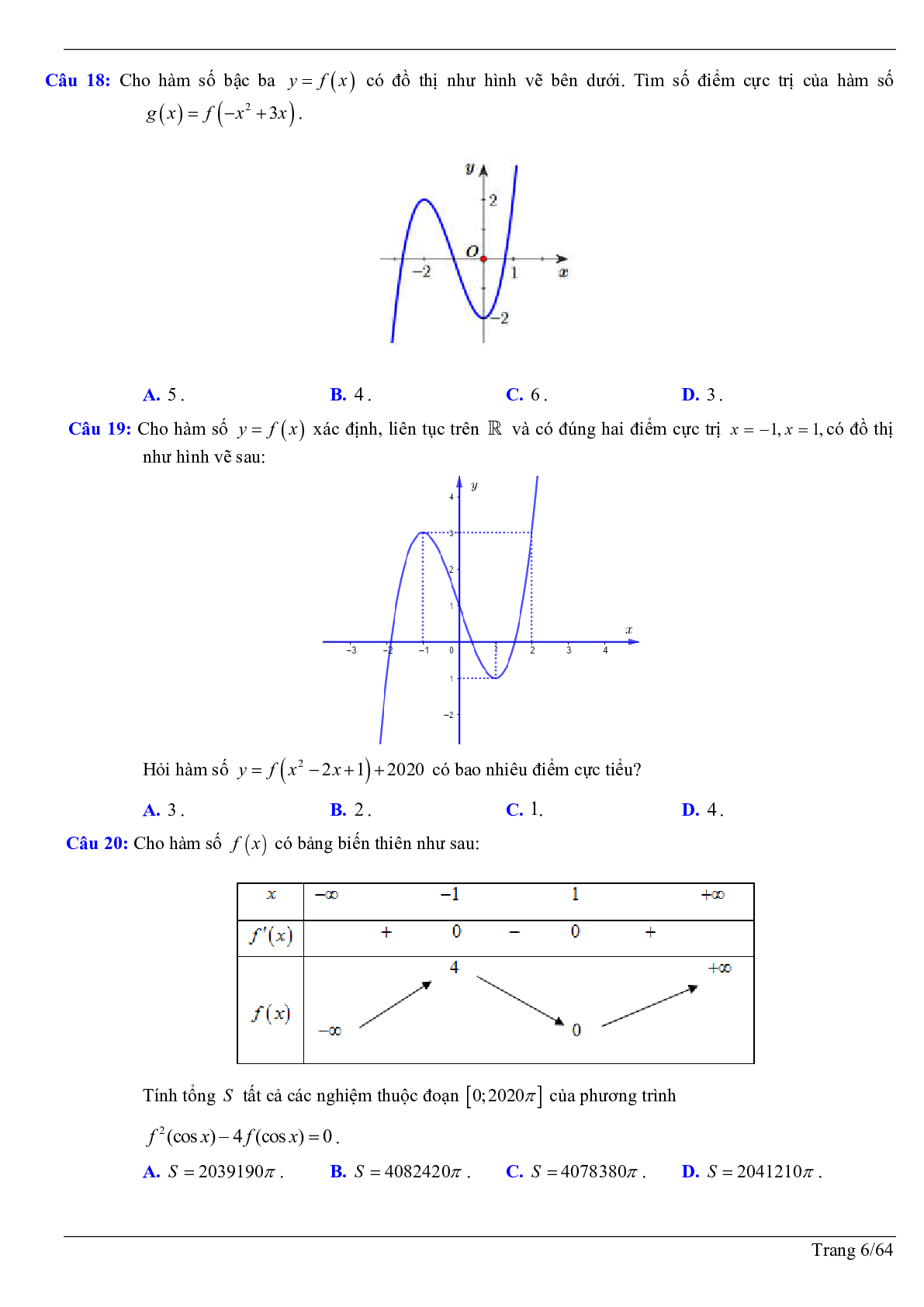
Câu 18: Cho hàm số y = f(x) có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số là

A. M(0; 2)    B. N(-2; -14)

C. P(2; -14)     D. N(-2; -14) và P(2; -14)

Đáp án

Câu 19: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên

Mệnh đề nào sau đây là đúng?

A. Hàm số có đúng hai cực trị

B. Hàm số có điểm cực tiểu là -2

C. Hàm số có giá trị cực đại bằng 0.

D. Hàm số đạt cực đại tại x = 0 đạt cực tiểu tại x = -1 và x = 1

Đáp án

Câu 20: Tìm a, b, c sao cho hàm số y = x³ + ax² + bx + c có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .

Đáp án

Sử dụng giả thiết và điều kiện cần của cực trị ta có

y(1) = 0; y'(-1) = 0; y(-1) = 0

Trong đó , y' = 3x² + 2ax + b

Từ đó suy ra:

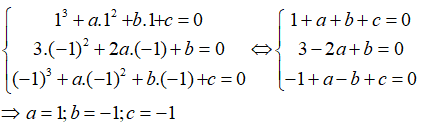
Với a = 1; b = -1; c = -1 thì hàm số đã cho trở thành y = x³ + x² - x - 1

Ta có y' = 3x² + 2x - 1, y'' = 6x + 2. Vì y''=(-1) = -4 < 0 nên hàm số đạt cực đại tại x = -1 . Vậy a = 1; b = -1; c = -1 là các giá trị cần tìm.

Chọn đáp án C.

Bài giảng Toán học 12 Bài 2: Cực trị của hàm số