Tailieumoi.vn xin giới thiệu chuyên đề Hai mặt phẳng vuông góc thuộc chương trình Toán 11. Chuyên đề gồm 77 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.
Chuyên đề Hai mặt phẳng vuông góc
Phần 1: Bài tập trắc nghiệm lý thuyết hai mặt phẳng vuông góc cực hay
1. Góc giữa hai mặt phẳng
a. Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai đường thẳng đó.
b. Cách xác định góc giữa hai mặt phẳng:
Giả sử (P) ∩ (Q) = c. Từ I ∈ c, dựng
c. Diện tích hình chiếu của một đa giác
Gọi S là diện tích của đa giác (H) trong (P), S' là diện tích của hình chiếu (H') của (H) trên (Q), φ = ((P), (Q)) . Khi đó: S' = S.cosφ
2. Hai mặt phẳng vuông góc
a. Định nghĩa:
Hai mặt phẳng được gọi là vuông góc nếu góc giữa hai đường thẳng đó bằng 90°. (P) ⊥ (Q) ⇔ ((P), (Q)) = 90°
b. Điều kiện để hai mặt phẳng vuông góc với nhau:
Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng đó vuông góc với nhau.
c. Tính chất của hai mặt phẳng vuông góc
+ Định lí: Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau thì bất kì đường thẳng a nào nằm trong (P) và vuông góc với giao tuyến của (P) và( Q) đều vuông góc với (Q)
+ Hệ quả 1: Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau và A là 1 điểm nằm trong (P) thì đường thẳng a đi qua điểm A và vuông góc với (Q) sẽ nằm trong (P).
+ Hệ quả 2: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
+ Hệ quả 3: Qua đường thẳng a không vuông góc với mặt phẳng (P) có duy nhất một mặt phẳng (Q) vuông góc với mp(P).
3. Hình lăng trụ đứng. Hình hộp chữ nhật và hình lập phương
a. Hình lăng trụ đứng : Là hình lăng trụ có cạnh bên vuông góc với mặt đáy
b. Hình lăng trụ đều: Là hình lăng trụ đứng có đáy là đa giác đều.
c. Hình hộp đứng: Là hình lăng trụ đứng có đáy là hình bình hành.
d. Hình hộp chữ nhật: là hình hộp đứng có đáy là hình chữ nhật.
e. Hình lập phương: Là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
4. Hình chóp đều và hình chóp cụt đều
Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu đáy của nó là đa giác đều và các cạnh bên bằng nhau.
Định nghĩa: Khi cắt hình chóp đều bởi một mặt phẳng song song với đáy để được một hình chóp cụt đó được gọi là hình chóp cụt đều.
Ví dụ 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Hướng dẫn giải
Chọn C
Đường thẳng thỏa mãn cần tìm là đường thẳng đi qua điểm A cho trước và vuông góc với mặt phẳng (P) cho trước. Đây là đường thẳng cố định.
Ví dụ 2: Chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Cho hai đường thẳng a và b vuông góc với nhau, mặt phẳng nào vuông góc với đường này thì song song với đường kia.
B. Cho đường thẳng a ⊥ (α) , mọi mặt phẳng (β) chứa a thì (β) ⊥ (α) .
C. Cho hai đường thẳng chéo nhau a và b, luôn luôn có mặt phẳng chứa đường này và vuông góc với đường thẳng kia.
D. Cho hai đường thẳng a và b vuông góc với nhau, nếu mặt phẳng (α) chứa a và mặt phẳng (β) chứa b thì (α) ⊥ (β) .
Hướng dẫn giải
Chọn B
Định lí: Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng đó vuông góc với nhau .
Ví dụ 3: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một cạnh bên vuông góc với đáy. Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau mệnh đề nào đúng?
A. Có ba cặp mặt phẳng vuông góc với nhau
B. Có hai cặp mặt phẳng vuông góc với nhau
C. Có năm cặp mặt phẳng vuông góc với nhau
D. Có bốn cặp mặt phẳng vuông góc với nhau
Hướng dẫn giải
Xét hình chóp S.ABCD có đáy là hình vuông và SA ⊥ (ABCD)
+ Do SA ⊂ (SAB) và SA ⊥ (ABCD) nên (SAB) ⊥ (ABCD)
+ Do SA ⊂ (SAD) và SA ⊥ (ABCD) nên (SAD) ⊥ (ABCD)
+ Do AD ⊥ SA, AD ⊥ AB nên AD ⊥ ( SAB)
AD ⊂ (SAD) và AD ⊥ (SAB) nên (SAD) ⊥ (SAB).
+ Chứng minh tương tự; ta có: (SAD) ⊥ (SCD) và (SAB) ⊥ (SBC).
⇒ có tất cả năm cặp mặt phẳng vuông góc với nhau.
Chọn C
Ví dụ 4: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
B. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Một mặt phẳng (P) và một đường thẳng a không thuộc (P) cùng vuông góc với đường thẳng b thì (P) // a .
Hướng dẫn giải
Chọn D
Ví dụ 5: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
Hướng dẫn giải
Chọn D
Định nghĩa: Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật. Khi đó tất cả 6 mặt của hình hộp đều là hình chữ nhật
Hình hộp đứng : Là hình lăng trụ đứng có đáy là hình bình hành. Khi đó chỉ có 4 mặt của hình hộp là hình chữ nhật
Ví dụ 6: Trong các mệnh đề sau đây, hãy tìm mệnh đề đúng.
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
B. Nếu hai mặt vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.
C. Hai mặt phẳng (α) và (β) vuông góc với nhau và cắt nhau theo giao tuyến d. Với mỗi điểm A thuộc (α) và mỗi điểm B thuộc (β) thì ta có đường thẳng AB vuông góc với d.
D. Nếu hai mặt phẳng (α) và (β) đều vuông góc với mặt phẳng (γ) thì giao tuyến d của (α) và (β) nếu có sẽ vuông góc với (γ)
Hướng dẫn giải
Chọn D
Đây là định lí.
Ví dụ 7: Cho hai mặt phẳng (α) và (β) vuông góc với nhau và gọi d = (α) ∩ (β).
I. Nếu a ⊂ (α) và a ⊥ d thì a ⊥ (β)
II. Nếu d' ⊥ (α) thì d' ⊥ d
III. Nếu b ⊥ d thì b ⊂ (α) hoặc b ⊂ (β)
IV. Nếu (γ) ⊥ d thì (γ) ⊥ (α) và (γ) ⊥ (β)
Các mệnh đề đúng là
A. I, II và III.
B. III và IV.
C. II và III.
D. I, II và IV.
Hướng dẫn giải
Chọn D.
Dựa theo tính chất hai mặt phẳng vuông góc nên suy ra : I ; II và IV đúng.
Ví dụ 8: Cho hình chóp S.ABC có đáy ABC là tam giác đều. Trong các mệnh đề sau, mệnh đề nào đúng?
A. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân đỉnh
B. S.ABC là hình chóp đều nếu góc giữa các mặt phẳng chứa các mặt bên và mặt phẳng đáy bằng nhau.
C. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân.
D. S.ABC là hình chóp đều nếu các mặt bên có diện tích bằng nhau.
Hướng dẫn giải
Chọn A
+ Định nghĩa: Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
+ Nếu hình chóp S.ABC có các mặt bên là các tam giác cân tại S thì SA = SB = SC.
Lại có đáy ABC là tam giác đều
⇒ S.ABC là hình chóp đều.
Ví dụ 9: Trong lăng trụ đều, khẳng định nào sau đây sai?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
Hướng dẫn giải
A. Vì lăng trụ đều nên các cạnh bằng nhau. Do đó đáy là đa giác đều.
B. Vì lăng trụ đều là lăng trụ đứng nên các mặt bên vuông góc với đáy.
C. Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên vuông góc với đáy.
D. Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên bằng nhau và cùng vuông góc với đáy. Do đó các mặt bên là những hình vuông.
Chọn D
Ví dụ 10: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Hướng dẫn giải
Chọn đáp án B
A sai vì đáy có thể là hình bình hành.
B đúng
C sai vì đáy có thể là hình bình hành
D sai vì đáy có thể là hình bình hành.
Ví dụ 11: Hình hộp ABCD.A'B'C'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?
A. Tất cả các cạnh đáy bằng nhau và cạnh bên vuông góc với mặt đáy.
B. Có một mặt bên vuông góc với mặt đáy và đáy là hình vuông.
C. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông.
D. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc với mặt đáy.
Hướng dẫn giải
Chọn đáp án C
+ Định nghĩa: Hình lăng trụ tứ giác đều là hình lăng trụ đứng có đáy là hình vuông.
+ Do đó; để hình hộp ABCD.A’B’C’D’ trở thành hình lăng trụ tứ giác đều thì các mặt bên là hình chữ nhật và đáy là hình vuông .
Phần 2: Cách tính góc giữa hai mặt phẳng trong không gian cực hay
Để tính góc giữa hai mặt phẳng (α) và (β) ta có thể thực hiện theo một trong các cách sau:
Cách 1. Tìm hai đường thẳng a; b lần lượt vuông góc với hai mặt phẳng (α) và (β). Khi đó góc giữa hai đường thẳng a và b chính là góc giữa hai mặt phẳng (α) và (β).
Cách 2. Sử dụng công thức hình chiếu: Gọi S là diện tích của hình (H) trong mp(α) và S’ là diện tích hình chiếu (H’) của (H) trên mp(β) thì S’ = S.cosφ
⇒ cosα ⇒ φ
Cách 3. Xác định cụ thể góc giữa hai mặt phẳng rồi sử dụng hệ thức lượng trong tam giác để tính.
+ Bước 1: Tìm giao tuyến Δ của hai mp
+ Bước 2: Chọn mặt phẳng (γ) vuông góc Δ
+ Bước 3: Tìm các giao tuyến (γ) với (α); (β)
⇒ ((α), (β)) = (a, b)
Ví dụ 1: Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là ∠CBD
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là ∠AIB
C. (BCD) ⊥ (AIB)
D. (ACD) ⊥ (AIB)
Hướng dẫn giải
+ Tam giác BCD cân tại B có I trung điểm đáy CD
⇒ CD ⊥ BI (1)
+ Tam giác CAD cân tại A cóI trung điểm đáy CD
⇒ CD ⊥ AI (2)
Từ (1) và (2) ⇒ CD ⊥ (ABI).
⇒ (BCD) ⊥ (ABI) Và (ACD) ⊥ (ABI);
Góc giữa hai mặt phẳng (ACD) và (BCD) là ∠AIB .
Vậy A: sai
Chọn A
Ví dụ 2: Cho tứ diện đều ABCD. Góc giữa (ABC) và (ABD) bằng α. Chọn khẳng định đúng trong các khẳng định sau?
Hướng dẫn giải
Đặt AB = a. Gọi I là trung điểm của AB.
Tam giác ABC đều cạnh a nên CI ⊥ AB và CI = a√3/2
Tam giác ABD đều nên DI ⊥ AB và DI = a√3/2
Do đó, ((ABC), (ABD)) = (CI, DI) = ∠CID = α
Tam giác CID có
Chọn A
Ví dụ 3: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Tính của góc giữa một mặt bên và một mặt đáy.
Hướng dẫn giải
Chọn C.
Gọi H là giao điểm của AC và BD.
+ Do S.ABCD là hình chóp tứ giác đều nên SH ⊥( ABCD)
Ta có: (SCD) ∩ (ABCD) = CD. Gọi M là trung điểm CD.
+ Tam giác SCD là cân tại S ; tam giác CHD cân tại H (Tính chất đường chéo hình vuông)
SM ⊥ CD và HM ⊥ CD
⇒ ((SCD), (ABCD)) = (SM, HM) = ∠SMH = α
Từ giả thiết suy ra tam giác SCD là tam giác đều cạnh a có SM là đường trung tuyến ⇒ SM = a√3/2
Ví dụ 4: Cho hình chóp S.ABC có hai mặt bên (SAB) và(SAC) vuông góc với mặt phẳng (ABC) , tam giác ABC vuông cân ở A và có đường cao AH (H ∈ BC) . Gọi O là hình chiếu vuông góc của A lên (SBC) . Khẳng định nào sau đây sai ?
A. SA ⊥ (ABC)
B. O ∈ SH
C. (SAH) ⊥ (SBC)
D. ((SBC), (ABC)) = ∠SBA
Hướng dẫn giải
Ví dụ 5: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠BAD = 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF)và (SBC) là
A. 90° B. 60° C. 30° D. 45°
Hướng dẫn giải
Tam giác BCD có BC = BD và ∠BCD = 60° nên tam giác BCD đều
Lại có E là trung điểm BC ⇒ DE ⊥ BC
Mặt khác, tam giác BDE có OF là đường trung bình
⇒ OF // DE ⇒ BC ⊥ OF (1).
+ Do SO ⊥ (ABCD) ⇒ BC ⊥ SO (2).
+ Từ (1) và (2), suy ra BC ⊥ (SOF) ⇒ (SBC) ⊥ (sOF)
Vậy, góc giữa ( SOF) và( SBC) bằng 90°
Chọn A
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
A. 30° B. 90° C. 60° D. 45°
Hướng dẫn giải
Gọi H là chân đường vuông góc của S xuống mặt phẳng đáy (ABCD) (SH ⊥(ABCD))
+ Do SA = SB = SC = a nên hình chiếu vuông góc H của S lên mp(ABCD) là tâm đường tròn ngoại tiếp tam giác ABC.
+ Mà tam giác ABC cân tại B ( Vì BA = BC = a) ⇒ tâm H phải nằm trên BD ⇒ SH ⊂ (SBD)
Ví dụ 7: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng a. Gọi M là trung điểm SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
A. 90° B. 60° C. 45° D. 30°
Hướng dẫn giải
Gọi M’ là trung điểm OC.
Do S.ABCD là hình chóp tứ giác đều nên SO ⊥ (ABCD)
⇒ SO ⊥ OC.
Xét tam giác SOC vuông tại O đường trung tuyến OM có: OM = SC/2 = a/2
Chọn đáp án C
Ví dụ 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A đến BD bằng 2a/√5. Biết SA ⊥ (ABCD) và SA = 2a. Gọi α là góc giữa hai mặt phẳng (ABCD) và (SBD). Khẳng định nào sau đây sai?
A. (SAB) ⊥ (SAD)
B. (SAC) ⊥ (ABCD)
C. tanα = √5
D. α = ∠SOA
Hướng dẫn giải
Gọi AK là khoảng cách từ A đến BD
Khi đó:
Phần 3: Cách chứng minh hai mặt phẳng vuông góc trong không gian cực hay
* Chứng minh hai mặt phẳng vuông góc
Để chứng minh (P) ⊥ (Q), ta có thể chứng minh bởi một trong các cách sau:
- Chứng minh trong (P) có một đường thẳng a mà a ⊥ (Q).
- Chứng minh ((P), (Q)) = 90°
* Chứng minh đường thẳng vuông góc với mặt phẳng
Để chứng minh d ⊥ (P), ta có thể chứng minh bởi một trong các cách sau:
- Chứng minh d ⊂ (Q) với (Q) ⊥ (P) và d vuông góc với giao tuyến c của (P) và (Q).
- Chứng minh d = (Q) ∩ (R) với (Q) ⊥ (P) và (R) ⊥ (P).
- Sử dụng các cách chứng minh đã biết ở phần trước.
Ví dụ 1: Cho tứ diện ABCD có AB ⊥ (BCD) . Trong tam giác BDC vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK ⊥ AC tại K. Khẳng định nào sau đây sai ?
A. (ADC) ⊥ (ABE) B. (ADC) ⊥ (DFK)
C. (ADC) ⊥ (ABC) D. (BDC) ⊥ (ABE)
Hướng dẫn giải
Ta xét các phương án:
Chọn C
Ví dụ 2: Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC) . Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
A. (ABE) ⊥ (ADC) B. (ABD) ⊥ (ADC)
C. (ABC) ⊥ (DFK) D. (DFK) ⊥ (ADC)
Hướng dẫn giải
Chọn B
Ví dụ 3: Cho hình chóp S.ABC có SA ⊥ (ABC) và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?
A. H ∈ SB
B. H trùng với trọng tâm tam giác SBC.
C. H ∈ SC
D. H ∈ SI (I là trung điểm của BC).
Hướng dẫn giải
Chọn D
Gọi I là trung điểm của BC
⇒ AI ⊥ BC mà BC ⊥ SA ⇒ BC ⊥ (SAI)
⇒ SI ⊥ BC (1)
Khi đó H là hình chiếu vuông góc của A lên (SBC) .
Suy ra AH ⊥ BC
Lại có: SA ⊥ BC
⇒ BC ⊥ (SAH) ⇒ BC ⊥ SH (2)
Từ (1) và (2) suy ra 3 điểm S; H; I thẳng hàng.
Chọn D.
Ví dụ 4: Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC) . Khẳng định nào sau đây sai?
A. SC ⊥ (ABC)
B. Nếu A’ là hình chiếu vuông góc của A lên ( SBC) thì A' ∈ SB .
C. (SAC) ⊥ (ABC)
D. BK là đường cao của tam giác ABC thì BK ⊥ (SAC)
Hướng dẫn giải
Chọn B
+ Ta có:
+ Gọi A’ là hình chiếu vuông góc của A lên (SBC)
khi đó AA' ⊥ (SBC) ⇒ AA' ⊥ BC ⇒ A' ∈ BC
Suy ra đáp án B sai.
Chọn B.
Ví dụ 5: Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC) , tam giác ABC vuông cân ở A và có đường cao AH. Gọi O là hình chiếu vuông góc của A lên (SBC) . Khẳng định nào sau đây đúng?
A. SC ⊥ (ABC)
B. (SAH) ⊥ (SBC)
C. O ∈ SC
D. Góc giữa (SBC) và (ABC) là góc ∠SBA
Hướng dẫn giải
Chọn B
Ta có:
Gọi H là trung điểm của BC ⇒ AH ⊥ BC (vì tam giác ABC vuông cân tại A).
mà BC ⊥ SA ⇒ BC ⊥ (SAH) ⇒ (SBC) ⊥ (SAH)
Khi đó O là hình chiếu vuông góc của A lên (SBC)
Thì suy ra O thuộc SH và ((SBC), (ABC)) = ∠SHA
Vậy đáp án B đúng
Ví dụ 6: Cho hình lập phương ABCD.A1B1C1D1 . Mặt phẳng (A1BD) không vuông góc với mặt phẳng nào dưới đây?
A. (AB1D) B. (ACC1A1) C. (ABD1) D. (A1BC1)
Hướng dẫn giải
* Gọi I = AB1 ∩ A1B
Tam giác A1BD đều có DI là đường trung tuyến nên
Tam giác A1BD đều có BJ là đường trung tuyến nên BJ ⊥ A1D .
Chọn D
Ví dụ 7: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây sai?
A. Tam giác AB’C là tam giác đều.
B. Nếu α là góc giữa AC’ và ( ABCD) thì cosα = √(2/3) .
C. ACC'A' là hình chữ nhật có diện tích bằng 2a2.
D. Hai mặt (AA'C'C) và (BB'D'D) ở trong hai mặt phẳng vuông góc với nhau.
Hướng dẫn giải
Chọn C
Từ giả thiết tính được AC = a√2
Mặt khác vì ABCD.A'B'C'D' là hình lập phương nên suy ra ∠AA'C' = 90°
Xét tứ giác ACC'A' có
⇒ ACC'A' là hình chữ nhật có các cạnh a và a√2.
Diện tích hình chữ nhật ACC’A’ là :
S = a.a.√2 = a2√2 (đvdt)
⇒ đáp án C sai.
Phần 4: Cách tính độ dài đoạn thẳng trong không gian cực hay
Ví dụ 1: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c. Độ dài đường chéo AC' là
Hướng dẫn giải:
Áp dụng định lí Py-ta-go vào tam giác vuông ABB’ ta có :
Do ABCD.A’B’C’D’ là hình lập phương nên:
B’C’ ⊥ (ABB'A') ⇒ B'C ⊥ AB'
Áp dụng định lí Py-ta-go vào tam giác vuông AB’C’ ta có:
Vậy đường chéo hình hộp chữ nhật
Chọn A
Ví dụ 2: Cho hình hộp ABCD.A'B'C'D' có AB = a, BC = b, CC’ = c. Nếu AC' = BD' = B'D = √(a2 + b2 + c2) thì hình hộp là
A. Hình lập phương
B. Hình hộp chữ nhật
C. Hình hộp thoi
D. Hình hộp đứng
Hướng dẫn giải:
Nếu AC’= BD’ ⇒ hình bình hành ABC’D’ là hình chữ nhật
Nếu BD’= B’D ⇒ hình bình hành BDD’B’ là hình chữ nhật
Nếu AC’= B’D ⇒ hình bình hành ADC’B’ là hình chữ nhật
⇒ nếu AC’ = BD’ = B’D thì hình hộp là hình hộp chữ nhật.
Chọn B
Ví dụ 3: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai mặt phẳng đó hai điểm A và B sao cho AB= 8. Gọi C là một điểm trên (P) , D là một điểm trên (Q) sao cho AC; BD cùng vuông góc với giao tuyến d và AC = 6; BD = 24. Độ dài CD là:
A. 20 B. 22 C. 30 D. 26
Hướng dẫn giải:
Tam giác ABC vuông tại A nên
Ví dụ 4: Cho ba tia Ox, Oy, Oz vuông góc nhau từng đôi một. Trên Ox, Oy, Oz lần lượt lấy các điểm A, B, C sao cho OA = OB = OC = a. Khẳng định nào sau đây sai?
A. O.ABC là hình chóp đều
B. Tam giác ABC có diện tích
C. Tam giác ABC có chu vi
D. Ba mặt phẳng (OAB), (OBC) và (OAC) vuông góc với nhau từng đôi một.
Hướng dẫn giải:
Chọn C
+ Áp dụng định lý Pytago trong tam giác OAB vuông tại O ta có:
AB2 = OA2 + OB2 = a2 + a2 = 2a2 ⇒ AB = a√2
Hoàn toàn tương tự ta tính được BC = AC = a√2.
⇒ Tam giác ABC là tam giác đều.
Mặt khác theo giả thiết OA = OB = OC = a
⇒ Các mặt bên của hình chóp O. ABC là các tam giác cân tại O còn đáy ABC là tam giác đều
⇒ O.ABC là hình chóp đều ⇒ phương án A đúng.
+ Chu vi tam giác BAC là:
⇒ phương án C sai
+ Nửa chu vi tam giác ABC là: p = 3a(√2)/2 .
Áp dụng công thức Hê - rông, diện tích tam giác ABC là:
Chọn C
Ví dụ 5: Cho hình thoi ABCD có cạnh bằng a và ∠A = 60° . Trên đường thẳng vuông góc với mặt phẳng (ABDC) tại O (O là tâm của ABCD), lấy điểm S sao cho tam giác SAC là tam giác đều. Khẳng định nào sau đây đúng?
A. S.ABCD là hình chóp đều.
B. Hình chóp S.ABCD có các mặt bên là các tam giác cân.
C. SO = 3a/2
D. SA và SB hợp với mặt phẳng (ABCD) những góc bằng nhau.
Hướng dẫn giải:
Chọn C
+ Xét tam giác ABD có ∠ = 60° và AB = AD = a
⇒ tam giác ABD là tam giác đều cạnh a.
+ Vì O là tâm của ABCD nên suy ra AO là đường trung tuyến trong tam giác ABD đều cạnh a nên tính được
+ Mặt khác theo giả thiết SAC là tam giác đều ⇒ SA = SC = AC = a√3
Áp dụng định lí Py ta go vào tam giác SOA ta có:
SO = √(SA2 - AO2) = 3a/2
⇒ C đúng
Ví dụ 6: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a; CD = 2x. Gọi I và J lần lượt là trung điểm của AB và CD. Tính IJ theo a và x?
Hướng dẫn giải:
+ Tam giác ACD cân tại A có AJ đường trung tuyến nên đồng thời là đường cao: AJ ⊥ CD (1)
Tam giác BCD cân tại B có BJ là đường trung tuyến nên đồng thời là đường cao : BJ ⊥ CD (2)
Vậy tam giác ABJ vuông tại J
Phần 5: Cách xác định thiết diện chứa một đường thẳng và vuông góc với một mặt phẳng
Cho mặt phẳng (α) và đường thẳng a không vuông góc với (α). Xác định mặt phẳng (β) chứa a và vuông góc với (α)
- Để giải bài toán này ta làm theo các bước sau:
+ Chọn một điểm A ∈ a
+ Dựng đường thẳng b đi qua A và vuông góc với (α). Khi đó mp(a; b) chính là mặt phẳng (β).
Ví dụ 1: Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A; B cùng thuộc Δ và lấy C trên (P), D trên (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua A và vuông góc với CD là hình gì?
A. Tam giác cân. B. Hình vuông
C. Tam giác đều. D. Tam giác vuông
Hướng dẫn giải
Gọi I là trung điểm của BC
Vì tam giác ABC vuông cân tại A nên AI ⊥ BC
Ta có
Trong (ACD) , dựng đường thẳng đi qua A và vuông góc với CD cắt CD tại H
Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) là tam giác AHI.
Vì AI ⊥ (BCD) ⇒ AI ⊥ HI nên tam giác AHI là tam giác vuông tại I.
Chọn D
Ví dụ 2: Cho hình chóp S.ABCD, đáy ABCD là hình vuông, SA ⊥ (ABCD). Gọi (α) là mặt phẳng chứa AB và vuông góc với (SCD), (α) cắt chóp S.ABCD theo thiết diện là hình gì?
A. hình bình hành
B. hình thang vuông
C. hình thang không vuông
D. hình chữ nhật
Hướng dẫn giải
Dựng AH ⊥ CD
Ta có
Từ đó thiết diện là hình thang ABKH
Mặt khác AB ⊥ (SAD) nên AB ⊥ AH
Vậy thiết diện là hình thang vuông tại A và H
Chọn đáp án B
Ví dụ 3: Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có AB = a ; AD = 2a ; SA vuông góc với đáy và SA = a. Gọi (P) là mặt phẳng qua SO và vuông góc với (SAD). Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?
Hướng dẫn giải
Trong (ABCD) dựng đường thẳng d qua O và d // AB.
Gọi M và N lần lượt là giao điểm của d với BC và AD.
Ta có : AB ⊥ AD và AB ⊥ SA nên AB ⊥ (SAD)
Lại có: MN // AB ⇒ MN ⊥ (SAD).
⇒ ( SMN) ⊥ (SAD) (1)
Mà SO ⊂ (SMN) nên (P) chính là (SMN).
⇒ Thiết diện của hình chóp cắt bởi mp (P) là tam giác SMN.
Do MN ⊥ (SAD) nên MN ⊥ SN; tam giác SMN vuông tại N.
Ví dụ 4: Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A; B cùng thuộc Δ và lấy C trên (P), D trên (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD = a. Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua A và vuông góc với CD là?
Hướng dẫn giải
Chọn C
Ta có:
Gọi H là trung điểm BC, ta có
Trong mặt phẳng (BCD), kẻ HI ⊥ CD thì ta có CD ⊥ (AHI)
Khi đó mặt phẳng (α) cắt tứ diện ABCD theo thiết diện là tam giác AHI
Mặt khác tam giác ABC vuông cân tại A nên BC = a√2 ⇒ AH = a√2/2
Trong tam giác BCD, kẻ đường cao BK thì BK = a√2/√3 và HI = a/√6
Vậy: thiết diện cần tìm là tam giác AHI vuông tại H và có diện tích S = a2√3/12
Ví dụ 5: Cho hình lăng trụ đứng AbC.A'B'C' có đáy ABC là tam giác vuông tại A, với AB = c; AC = b , cạnh bên AA’ = h. Mặt phẳng (P) đi qua A’ và vuông góc với B’C. Thiết diện của lăng trụ cắt bởi mặt phẳng (P) có hình:
A. h1 và h2 B. h2 và h3 C. h2 D. h1
Hướng dẫn giải
Gọi (P) là mặt phẳng đi qua A’ và vuông góc với BC.
Từ A’ ta dựng A'K' ⊥ B'C', Vì (ABC) ⊥ (BCC'B') nên A'K' ⊥ B'C' ⇒ A'K' ⊥ (BCC'B') ⇒ A'K' ⊥ BC' (1)
Mặt khác trong mặt phẳng (BCC'B') dựng K'x ⊥ B'C và cắt BB’ tại 1 điểm N(2) Từ (1) và (2) ta có :
Chọn đáp án A
Bài toán về hai mặt phẳng vuông góc
Lý thuyết và bài tập hai mặt phẳng vuông góc
Bài 4. Hai mặt phẳng vuông góc
A. Lý thuyết
I. Góc giữa hai mặt phẳng.
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Tức là \[\left\{ {\begin{array}{*{20}{c}}{(\alpha ) \bot (P)}\\{(\beta ) \bot (Q)}\end{array}} \right. \Rightarrow \left( {(P),(Q)} \right) = (a,b)\]
Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói góc giữa hai mặt phẳng đó bằng 00.
Diện tích hình chiếu \[S' = S\cos \varphi \]
Trong đó S là diện tích đa giác nằm trong (a), S' là diện tích đa giác nằm trong (b) còn j là góc giữa (a) và (b)
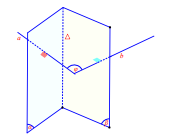
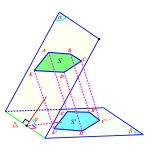
Nhận xét: Trong thực hành để xác định góc của hai mặt phẳng ta chỉ cần làm như sau: Bước 1 : Tìm giao tuyến D = (a) Ç ( b)
Bước 2 : Lấy một điểm M Î (b).
Dựng hình chiếu H của M trên (a) hay MH ^ mp(a)
(Trong bước này MH gọi là đường vuông góc với mặt phẳng đáy. Thông thường đề bài cho sẵn và H gọi là chân đường vuông góc)
Bước 3 : Lấy chân đường vuông góc là H và dựng HN ^ D (Bước này gọi là bước dựng lần kẻ thứ nhất)
Bước 4 : Ta chứng minh MN ^ D.
Bước 5 : Kết luận \[\left( {(P),(Q)} \right) = (HN,MN) = HNM = \varphi \]
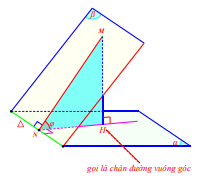
Ví dụ 1. Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại A, AB = AC = a; SA = a và vuông góc với đáy.
a). Tính góc giữa hai mặt phẳng (SBC) và (ABC).
b). Tính góc giữa hai mặt phẳng (SAC) và (SBC)
II. Hai mặt phẳng vuông góc.
1. Định nghĩa.
Hai mặt phẳng vuông góc với nhau nếu góc giữa chúng bằng 900.
Kí hiệu: \[(P) \bot (Q) \Leftrightarrow \left( {(P),(Q)} \right) = {90^0}\]
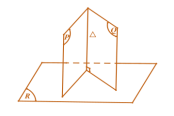
2. Tính chất.
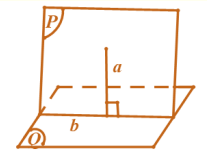
Tính chất 1. Hai mặt phẳng vuông góc với nhau khi và chỉ khi trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia.
Kí hiệu: \[\left\{ {\begin{array}{*{20}{c}}{a \subset (P)}\\{a \bot (Q)}\end{array}} \right. \Rightarrow (P) \bot (Q)\].
Nhận xét. Tính chất này giúp cho ta chứng minh được hai mặt phẳng vuông góc với nhau.
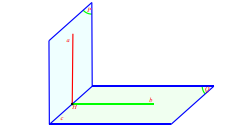
Tính chất 2. Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
Kí hiệu: \[\left\{ {\begin{array}{*{20}{c}}{(P) \bot (Q)}\\{a \subset (P)}\\{b = (P) \cap (Q)}\\{a \bot b}\end{array}} \right. \Rightarrow a \bot (Q)\]
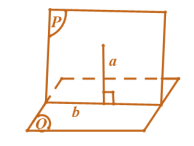
Tính chất 3. Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Nếu từ một điểm thuộc mp (P) dựng một đường thẳng vuông góc với mp (Q) thì đường thẳng này nằm trong (P)
Kí hiệu: \[\left\{ {\begin{array}{*{20}{c}}{A \in (P)}\\{(P) \bot (Q)}\\{A \in a \bot (Q)}\end{array} \Rightarrow } \right.a \subset (P)\].
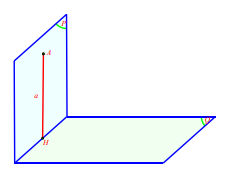
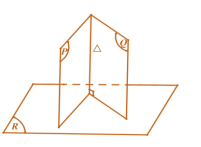
Tính chất 4. Nếu hai mặt phẳng cắt nhau cùng vuông góc với một mặt phẳng thì giao tuyến của chúng củng vuông góc với mặt phẳng đó
Kí hiệu: \[\left\{ {\begin{array}{*{20}{c}}{(P) \bot (R)}\\{(Q) \bot (R)}\\{(P) \cap (Q) = \Delta }\end{array} \Rightarrow } \right.\Delta \bot (R)\]
3. Ví dụ minh họa.
Ví dụ 2. Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy. Gọi M là trung điểm AC . Chứng minh (SAB) ^ (SBC) và (SBM) ^ (SAC).
Ví dụ 3. Cho tam giác ABC. Vẽ BB' và CC' cùng vuông góc với mặt phẳng (ABC) . Gọi H, K lần lượt là hình chiếu vuông góc của A trên BC, B'C' . Chứng minh ( AB'C') ^ (AHK).
III. Hình lăng trụ đứng, hình hộp chữ nhật.
1. Hình lăng trụ đứng.
Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với hai mặt đáy.
Các mặt bên là các hình chữ nhật.
Các mặt bên vuông góc với hai đáy.
Lăng trụ đứng có đáy là đa giác đều được gọi là lăng trụ đều.
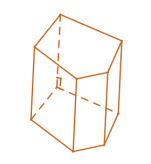
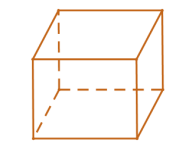
2. Hình hộp chữ nhật.
Hình hộp chữ nhật là hình lăng trụ đứng có đáy là hình chữ nhật.
Tất cả các mặt đều là hình chữ nhật
Đường chéo \[d = \sqrt {{a^2} + {b^2} + {c^2}} \] với a,b,c là ba kích thước.
3. Hình hộp lập phương.
Hình lập phương là hình hộp chữ nhật có đáy và các mặt bên đều là hình vuông.
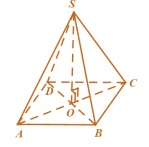
4. Hình chóp đều và hình chóp cụt đều.
Hình chóp đều là hình chóp có đáy là một đa giác đều và chân đường cao trùng với tâm của đa giác đáy.
Các cạnh bên của hình chóp đều tạo với đáy các góc bằng nhau
Các mặt bên của hình chóp đều là các tam giác cân bằng nhau.
Các mặt bên của hình chóp đều tạo với đáy các góc bằng nhau.
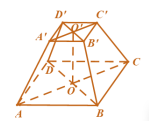
Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với đáy cắt tất cả các cạnh bên của hình chóp được gọi là hình chóp cụt đều.
Hai đáy của hình chóp cụt đều là hai đa giác đồng dạng.
Ví dụ 4. Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi K là hình chiếu của C trên BD, H là hình chiếu của C trên C'K. Chứng minh (CDH) ^ (C'BD).
Ví dụ 5. Cho hình lăng trụ đứng ABC.A¢B¢C¢ có AB = BC = a, AC =\[a\sqrt 2 \]
1). Chứng minh rằng: BC ^ AB¢ .
2). Gọi M là trung điểm của AC. Chứng minh (BC¢M¢) ^ (ACC’A’).
3). Tính khoảng cách giữa BB¢ và AC¢ .
B. Phân dạng và bài tập minh họa.
Dạng 1. Chứng minh hai mặt phẳng vuông góc với nhau.
1.Phương pháp: Để chứng minh hai mặt phẳng (P) và (Q) vuông góc với nhau ta có thể dùng một trong các cách sau:
Cách 1. Chứng minh trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia.
Kí hiệu: \[\left\{ {\begin{array}{*{20}{c}}{a \subset (P)}\\{a \bot (Q)}\end{array}} \right. \Rightarrow (P) \bot (Q)\]
Cách 2. Xác định góc giữa hai mặt phẳng, rồi tính trực tiếp góc đó bằng 900.
Kí hiệu: \[\left( {(\alpha ),(\beta )} \right) = {90^0} \Leftrightarrow (\alpha ) \bot (\beta )\].
Cách 3. Tìm hai vec tơ \[\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\], lần lượt vuông góc với các mặt phẳng (a),(b) rồi chứng minh \[\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\].
2. Bài tập minh họa:
Bài tập 1. Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Các tam giác SAC và SBD cân tại S. Gọi O là tâm hình thoi. Chứng minh SO ^ (ABCD) và (SAC) ^ (SBD).
Bài tập 2. Cho hình chóp S. ABCD có cạnh SA = a, các cạnh còn lại bằng b .
a). Chứng minh (SAC) ^(ABCD) và (SAC) ^ (SBD).
b). Tính đường cao của hình chóp S. ABCD theo a,b
c). Tìm sự liên hệ giữa a và b để S. ABCD là một hình chóp đều.





