Bài 4 trang 97 Toán 8 Tập 1 Cánh diều | Giải bài tập Toán lớp 8

Van Anh Ngày: 09-08-2024 Lớp 8

1.6 K

Với giải Bài 4 trang 97 Toán lớp 8 Tập 1 Cánh diều chi tiết trong Bài 1: Định lí Pythagore giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 1: Định lí Pythagore

Bài 4 trang 97 Toán 8 Tập 1: Cho một tam giác đều cạnh a.

a) Tính độ dài đường cao của tam giác đó theo a.

b) Tính diện tích của tam giác đó theo a.

Lời giải:

Giả sử ABC là tam giác đều cạnh a (hình vẽ).

Bài 4 trang 97 Toán 8 Tập 1 Cánh diều | Giải Toán 8

a) Vẽ đường cao AH của tam giác đều ABC.

Khi đó H là trung điểm của BC nên HB = HC = $\frac{1}{2} a$ .

Xét tam giác AHC vuông tại H, theo định lí Pythagore ta có:

AC² = AH² + HC²

Suy ra AH² = AC² – HC²

$= a^{2} - {(\frac{1}{2} a)}^{2} = a^{2} - \frac{1}{4} a^{2} = \frac{3}{4} a^{2} = {(\frac{\sqrt{3}}{2})}^{2} . a^{2} = {(\frac{a \sqrt{3}}{2})}^{2}$

Do đó $A H = \frac{a \sqrt{3}}{2}$ .

b) Diện tích của tam giác ABC là:

$S = \frac{1}{2} . A H . B C = \frac{1}{2} . \frac{a \sqrt{3}}{2} . a = \frac{a^{2} \sqrt{3}}{4}$ (đơn vị diện tích).

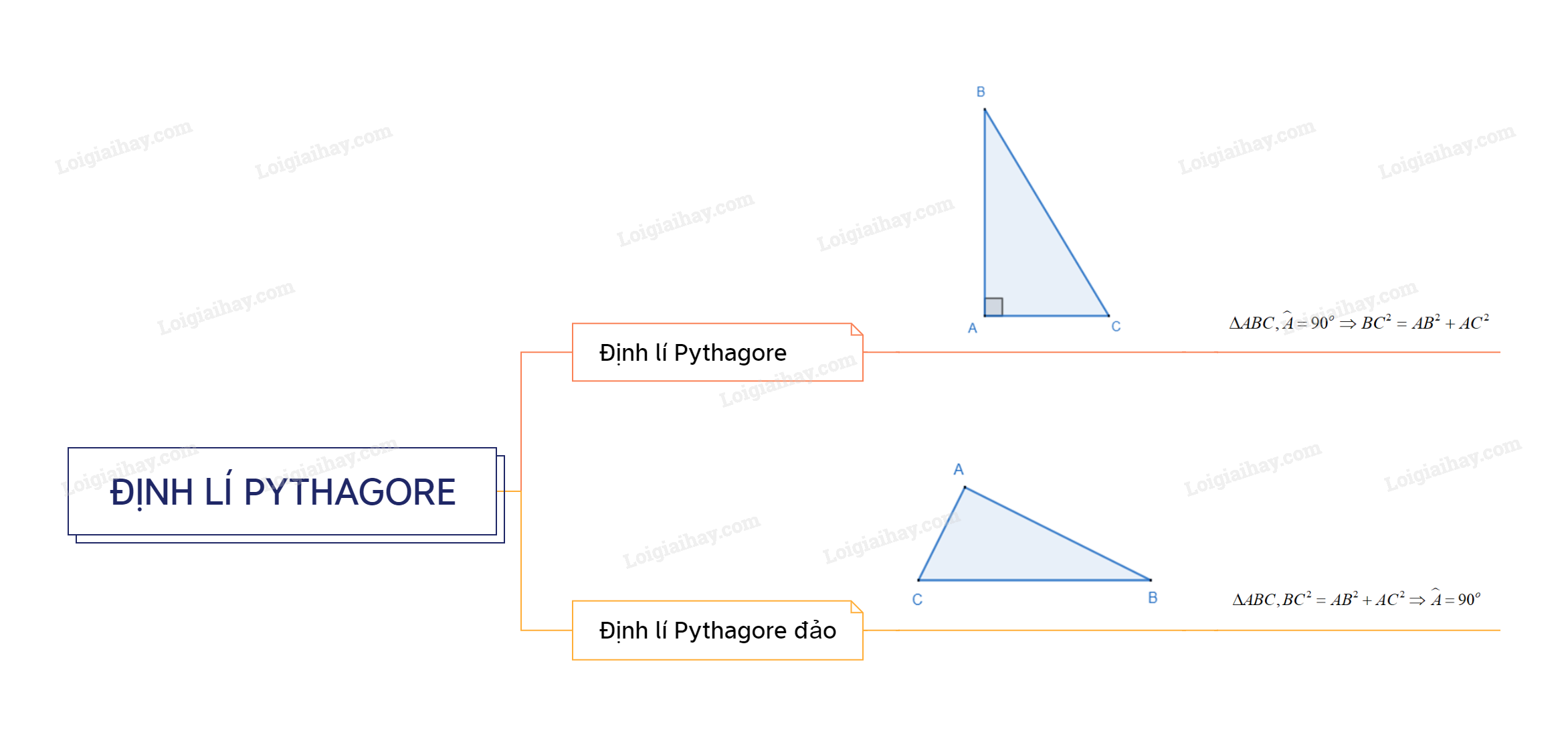
Sơ đồ tư duy Định lí Pythagore.

Xem thêm các lời giải bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:

Khởi động trang 94 Toán 8 Tập 1: Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại....

Hoạt động 1 trang 94, 95 Toán 8 Tập 1: Thực hiện các hoạt động sau:...

Luyện tập 1 trang 95 Toán 8 Tập 1: Tính độ dài đường chéo của hình vuông có độ dài cạnh là a...

Hoạt động 2 trang 95 Toán 8 Tập 1: Thực hiện các hoạt động sau:....

Luyện tập 2 trang 96 Toán 8 Tập 1: Tam giác có ba cạnh là 20 cm, 21 cm, 29 cm có phải là tam giác vuông hay không?....

Bài 1 trang 96 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Tìm độ dài cạnh còn lại trong mỗi trường hợp sau:....

Bài 2 trang 96 Toán 8 Tập 1: Tìm giác có độ dài ba cạnh trong mỗi trường hợp sau có phải là tam giác vuông hay không?...

Bài 3 trang 97 Toán 8 Tập 1: Cho tam giác vuông cân có độ dài cạnh góc vuông bằng 1 dm. Tính độ dài cạnh huyền của tam giác đó.....

Bài 4 trang 97 Toán 8 Tập 1: Cho một tam giác đều cạnh a.....

Bài 5 trang 97 Toán 8 Tập 1: Hình 9 mô tả một thanh gỗ dài 3,5 m dựa vào một bức tường thẳng đứng.. Chân thanh gỗ cách mép tường một khoảng là 2,1 m. Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là bao nhiêu mét?.....

Bài 6 trang 97 Toán 8 Tập 1: Hình 10 mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiều cao của khung phía trước khoảng 7 m, chiều cao của khung phía sau là 6 m, hai khung cách nhau một khoảng là 5 m. Chiều dài của mái che sân khấu đó là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?.....

Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:

Chủ đề 2: Thực hành tạo dựng Hologram

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Từ khóa :

toán 8

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

135

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm