Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 13: Hai mặt phẳng song song chi tiết sách Toán 11 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 13: Hai mặt phẳng song song

Giải Toán 11 trang 88 Tập 1

Mở đầu trang 88 Toán 11 Tập 1: Các đầu bếp chuyên nghiệp luôn có kĩ năng dùng dao điêu luyện để thái thức ăn như rau, củ, thịt, cá,... thành các miếng đều nhau và đẹp mắt. Các nhát cắt cần tuân thủ nguyên tắc gì để đạt được điều đó?

Lời giải:

Sau bài học này ta giải quyết được câu hỏi trên như sau:

Các nhát cắt cần tuân thủ nguyên tắc là nằm trong các mặt phẳng song song với nhau.

1. Hai mặt phẳng song song

HĐ1 trang 88 Toán 11 Tập 1: Các mặt bậc thang trong Hình 4.40 gợi nên hình ảnh về các mặt phẳng không có điểm chung. Hãy tìm thêm một số ví dụ khác cũng gợi nên hình ảnh đó.

Lời giải:

- Các mặt của từng tầng trong giá để dép gợi nên hình ảnh về các mặt phẳng không có điểm chung.

- Mặt sàn và mặt trần nhà bằng gợi nên hình ảnh về các mặt phẳng không có điểm chung.

- Hai mặt đối diện của hộp diêm gợi nên hình ảnh về các mặt phẳng không có điểm chung.

...

Câu hỏi trang 88 Toán 11 Tập 1: Trong hình ảnh mở đầu, các nhát cắt có nằm trong các mặt phẳng song song hay không?

Lời giải:

Trong hình ảnh mở đầu, các nhát cắt nằm trong các mặt phẳng song song.

2. Điều kiện và tính chất của hai mặt phẳng song song

Giải Toán 11 trang 89 Tập 1

HĐ2 trang 89 Toán 11 Tập 1: Cho mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) (H.4.41).

Nếu (α) và (β) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?

Lời giải:

Do a song song với mặt phẳng (β) và a nằm trong mặt phẳng (α) nên (α) và (β) cắt nhau theo giao tuyến c song song với a. Lí luận tương tự, ta thấy c song song với b. Từ đó suy ra a song song với b hoặc a trùng với b (mâu thuẫn giả thiết).

Câu hỏi trang 89 Toán 11 Tập 1: Nếu không có điều kiện “hai đường thẳng cắt nhau” thì khẳng định trên còn đúng không?

Lời giải:

Giả sử hai đường thẳng a và b trùng nhau thì khi đó có thể xảy ra trường hợp hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến c song song với hai đường thẳng trùng nhau trên, do đó (α) và (β) không song song với nhau. Do vậy, nếu không có điều kiện “hai đường thẳng cắt nhau” thì khẳng định trên không đúng.

Luyện tập 1 trang 89 Toán 11 Tập 1: Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m, n lần lượt song song với hai đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD).

Lời giải:

Vì m // BC nên m // (BCD).

Vì n // BD nên n // (BCD).

mp(m, n) chứa hai đường thẳng cắt nhau m và n (cắt nhau tại A) cùng song song với mặt phẳng (BCD) nên mp(m, n) song song với mặt phẳng (BCD).

Vận dụng 1 trang 89 Toán 11 Tập 1: Một chiếc bàn có phần chân là hai khung sắt hình chữ nhật có thể xoay quanh một trục như trong Hình 4.43. Khi mặt bàn được đặt lên phần chân bàn thì mặt bàn luôn song song với mặt đất. Hãy giải thích tại sao.

Lời giải:

Đặt tên các đường thẳng như trong hình vẽ dưới đây.

Vì các khung sắt có dạng hình chữ nhật nên các cạnh đối diện của khung sắt song song với nhau, do đó a // c và b // d.

Vì c và d là các đường thẳng của chân bàn nằm trên mặt đất, nên a // c thì đường thẳng a song song với mặt đất và b // d thì đường thẳng b song song với mặt đất.

Mặt phẳng bàn chứa hai đường thẳng cắt nhau a và b cùng song song với mặt đất nên mặt phẳng bàn song song với mặt đất.

HĐ3 trang 89 Toán 11 Tập 1: Đặt một tấm bìa cứng lên một góc của mặt bàn nằm ngang (H.4.44) sao cho mặt bìa song song với mặt đất. Khi đó mặt bìa có trùng bới mặt bàn hay không?

Lời giải:

Mặt bàn nằm ngang thì song song với mặt đất. Khi tấm bìa cứng được đặt lên một góc của mặt bàn nằm ngang sao cho mặt bìa song song với mặt bàn thì mặt bìa trùng với mặt bàn.

Câu hỏi trang 89 Toán 11 Tập 1: Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì hai mặt phẳng đó có song song với nhau hay không? Vì sao?

Lời giải:

Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì hai mặt phẳng đó song song với nhau.

Chứng minh: Cho ba mặt phẳng (P), (Q), (R) phân biệt có (P) // (Q), (Q) // (R). Ta chứng minh (P) // (R).

Giải Toán 11 trang 90 Tập 1

Luyện tập 2 trang 90 Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc cạnh SA, SB, SC, SD sao cho $\frac{MA}{MS}=\frac{NB}{NS}=\frac{PC}{PS}=\frac{QD}{QS}=\frac{1}{2}$ . Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng.

Lời giải:

Xét tam giác SAB có $\frac{MA}{MS}=\frac{NB}{NS}=\frac{1}{2}$ hay $\frac{SM}{SA}=\frac{SN}{SB}=\frac{1}{3}$ , suy ra MN // AB (theo định lí Thalés). Do đó MN song song với mặt phẳng (ABCD). Tương tự, NP // BC nên NP song song với mặt phẳng (ABCD). Vậy mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN và NP cùng song song với mặt phẳng (ABCD) nên mặt phẳng (MNP) song song với mặt phẳng (ABCD). Lập lập tương tự ta có mặt phẳng (MPQ) cũng song song với mặt phẳng (ABCD).

Hai mặt phẳng (MNP) và (MPQ) cùng đi qua điểm M và cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng đó trùng nhau, tức là bốn điểm M, N, P, Q đồng phẳng.

HĐ4 trang 90 Toán 11 Tập 1: Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46).

a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).

b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?

Lời giải:

a) Giả sử mặt phẳng (R) không cắt mặt phẳng (Q), tức là hai mặt phẳng (R) và (Q) song song với nhau, mà mặt phẳng (P) song song với mặt phẳng (Q), do đó mặt phẳng (R) cũng song song với mặt phẳng (P) (hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau), mẫu thuẫn với giả thiết (R) cắt (P) theo giao tuyến a.

Vậy mặt phẳng (R) cắt mặt phẳng (Q).

b) Vì a và b cùng thuộc mặt phẳng (R) nên hai đường thẳng a và b không thể chéo nhau.

Hai đường thẳng a và b không có điểm chung, vì nếu chúng có điểm chung A thì hai mặt phẳng (P) và (Q) cũng có điểm chung A (mâu thuẫn với giả thiết (P) và (Q) song song với nhau). Vậy hai đường thẳng a và b không thể cắt nhau.

Giải Toán 11 trang 91 Tập 1

Luyện tập 3 trang 91 Toán 11 Tập 1: Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).

Lời giải:

Trong Ví dụ 2, ta đã chứng minh được hai mặt phẳng (MNPQ) và (ABCD) song song với nhau. Vì vậy hai giao tuyến của mặt phẳng (EMQ) với hai mặt phẳng (MNPQ) và (ABCD) song song với nhau. Ta có (EMQ) ∩ (MNPQ) = MQ. Trong mặt phẳng (MEQ), qua E vẽ đường thẳng song song với MQ cắt CD tại H (EH // MQ // AD) thì đường thẳng EH là giao tuyến của hai mặt phẳng (EMQ) và mặt phẳng (ABCD).

3. Định lí Thalès trong không gian

HĐ5 trang 91 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d' cắt ba mặt phẳng lần lượt tại A, B, C và A', B', C' (C khác C'). Gọi D là giao điểm của AC' và (Q) (H.4.48).

a) Các cặp đường thẳng BD và CC', B'D và AA' có song song với nhau không?

b) Các tỉ số $\frac{AB}{BC},\frac{AD}{D{C}^{\text{'}}}$ và $\frac{A^{\text{'}}{B}^{\text{'}}}{B^{\text{'}}{C}^{\text{'}}}$ có bằng nhau không?

Lời giải:

a) Mặt phẳng (ACC') lần lượt cắt hai mặt phẳng song song (Q) và (R) theo hai giao tuyến BD và CC'. Do đó, BD // CC'.

Mặt phẳng AC'A' lần lượt cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến AA' và B'D. Do đó, B'D // AA'.

b) Xét tam giác ACC' có BD // CC', theo định lý Thalés trong tam giác ta suy ra $\frac{AB}{BC}=\frac{AD}{D{C}^{\text{'}}}$

Tương tự, xét tam giác AA'C' có B'D // AA', ta suy ra $\frac{AD}{D{C}^{\text{'}}}=\frac{A^{\text{'}}{B}^{\text{'}}}{B^{\text{'}}{C}^{\text{'}}}$ .

Vậy $\frac{AB}{BC}=\frac{AD}{D{C}^{\text{'}}}=\frac{A^{\text{'}}{B}^{\text{'}}}{B^{\text{'}}{C}^{\text{'}}}$ .

Luyện tập 4 trang 91 Toán 11 Tập 1: Trong HĐ5, cho AB = 2 cm, BC = 4 cm và A'B' = 3 cm. Tính độ dài của đoạn thẳng B'C'.

Lời giải:

Theo định lí Thalès trong không gian, ta có $\frac{AB}{A^{\text{'}}{B}^{\text{'}}}=\frac{BC}{B^{\text{'}}{C}^{\text{'}}}$ .

Suy ra $B^{\text{'}}{C}^{\text{'}}=\frac{A^{\text{'}}{B}^{\text{'}}.BC}{AB}=\frac{3.4}{2}=6$ (cm).

4. Hình lăng trụ và hình hộp

HĐ6 trang 91 Toán 11 Tập 1: Các hình ảnh dưới đây có đặc điểm chung nào với hình lăng trụ đứng tam giác mà em đã học ở lớp 7?

Lời giải:

Các hình ảnh đã cho trên đều có chứa hai mặt nằm trong hai mặt phẳng song song, các mặt còn lại chứa các cạnh đối diện song song với nhau.

Giải Toán 11 trang 92

Câu hỏi trang 92 Toán 11 Tập 1: Hãy giải thích tại sao các mặt bên của hình lăng trụ là hình bình hành, từ đó suy ra các cạnh bên đôi một song song và có độ dài bằng nhau.

Lời giải:

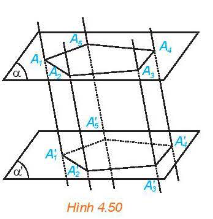
Xét mặt bên A₁A'₁A'₂A₂, theo lí thuyết, ta có A₁A'₁ // A₂A'₂, lại có mặt phẳng (A₁A'₁A'₂A₂) lần lượt cắt hai mặt phẳng song song (α) và (α') theo hai giao tuyến A₁A₂ và A'₁A'₂ nên A₁A₂ // A'₁A'₂. Do vậy, tứ giác A₁A'₁A'₂A₂ là hình bình hành (các cặp cạnh đối diện song song). Từ đó suy ra A₁A'₁ // A₂A'₂ và A₁A'₁ = A₂A'₂.

Chứng minh tương tự, ta có các mặt bên khác của hình lăng trụ là hình bình hành, từ đó suy ra các cạnh bên đôi một song song và có độ dài bằng nhau.

Luyện tập 5 trang 92 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M và M' lần lượt là trung điểm của cạnh BC và B'C'. Chứng minh rằng AMC.A'M'C' là hình lăng trụ.

Lời giải:

Vì các cạnh bên của hình lăng trụ ABC.A'B'C' đôi một song song nên AA', BB', CC' đôi một song song (1).

Ta có BB' // CC' nên BCC'B' là hình thang.

Vì M và M' lần lượt là trung điểm của cạnh BC và B'C' nên MM' là đường trung bình của hình thang BCC'B', suy ra MM', BB', CC' đôi một song song (2).

Từ (1) và (2) suy ra MM', AA', CC' đôi một song song.

Mặt phẳng (ABC) song song với mặt phẳng (A'B'C') nên mặt phẳng (AMC) song song với mặt phẳng (A'M'C').

Do vậy, AMC.A'M'C' là hình lăng trụ.

HĐ7 trang 92 Toán 11 Tập 1: Hình ảnh nào trong HĐ6 gợi nên hình ảnh về hình lăng trụ có đáy là hình bình hành?

Lời giải:

Hình ảnh thứ hai từ trái sang phải trong HĐ6 gợi nên hình ảnh về hình lăng trụ có đáy là hình bình hành.

Giải Toán 11 trang 93 Tập 1

Luyện tập 6 trang 93 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng hai mặt phẳng (ADD'A') và (BCC'B') song song với nhau.

Lời giải:

Hình hộp ABCD.A'B'C'D' có hai đáy ABCD và A'B'C'D' là các hình bình hành.

Ta có: AD // BC (do ABCD là hình bình hành), do đó AD // (BCC'B').

Lại có: AA' // BB' (các cạnh bên của hình hộp), do đó AA' // (BCC'B').

Mặt phẳng (ADD'A') chứa hai đường thẳng cắt nhau AD và AA' cùng song song với mặt phẳng (BCC'B') nên hai mặt phẳng (ADD'A') và (BCC'B') song song với nhau.

Vận dụng 2 trang 93 Toán 11 Tập 1: Để xác định mực nước trong một chiếc bể có dạng hình hộp, bác Hà đặt một thanh gỗ đủ dài vào trong bể sao cho một đầu của thanh gỗ dựa vào mép của nắp bể, đầu còn lại nằm trên đáy bể (H.4.53). Sau đó bác Hà rút thanh gỗ ra ngoài và tính tỉ lệ giữa độ dài của phần thanh gỗ bị ngâm trong nước và độ dài của cả thanh gỗ. Tỉ lệ này chính bằng tỉ lệ giữa mực nước và chiều cao của bể. Hãy giải thích vì sao.

Lời giải:

Vì bể nước có dạng hình hộp nên nắp bể và đáy bể nằm trong hai mặt phẳng song song. Khi mặt nước yên lặng thì mặt nước, nắp bể và đáy bể nằm trong ba mặt phẳng đôi một song song. Khi đó, thanh gỗ và chiều cao của bể đóng vai trò như hai đường thẳng phân biệt cắt ba mặt phẳng đôi một song song trên. Vậy áp dụng định lí Thalés trong không gian, ta khẳng định được tỉ lệ giữa mực nước và chiều cao của bể chính là tính tỉ lệ giữa độ dài của phần thanh gỗ bị ngâm trong nước và độ dài của cả thanh gỗ.

Bài tập

Bài 4.21 trang 93 Toán 11 Tập 1: Trong không gian cho ba mặt phẳng phân biệt (P), (Q), (R). Những mệnh đề nào sau đây là đúng?

a) Nếu (P) chứa một đường thẳng song song với (Q) thì (P) song song với (Q).

b) Nếu (P) chứa hai đường thẳng song song với (Q) thì (P) song song với (Q).

c) Nếu (P) và (Q) song song với (R) thì (P) song song với (Q).

d) Nếu (P) và (Q) cắt (R) thì (P) và (Q) song song với nhau.

Lời giải:

a) Mệnh đề a) là mệnh đề sai vì hai mặt phẳng (P) và (Q) có thể cắt nhau theo giao tuyến b song song với đường thẳng a nằm trong (P).

b) Mệnh đề b) là mệnh đề sai vì thiếu điều kiện hai đường thẳng đó phải cắt nhau.

c) Mệnh đề c) là mệnh đề đúng vì (P) và (Q) là hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba là mặt phẳng (R) thì (P) và (Q) song song với nhau.

d) Mệnh đề d) là mệnh đề sai vì (P) và (Q) cắt (R) thì (P) và (Q) có thể cắt nhau.

Giải Toán 11 trang 94 Tập 1

Bài 4.22 trang 94 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AA', BB', CC'. Chứng minh rằng mặt phẳng (MNP) song song với mặt phẳng (ABC).

Lời giải:

Vì ABC.A'B'C' là hình hình lăng trụ tam giác nên ABB'A' và BCC'B' là các hình bình hành hay cũng là các hình thang.

Vì M, N lần lượt là trung điểm của các cạnh AA', BB' nên MN là đường trung bình của hình thang ABB'A', do đó MN // AB, suy ra MN song song với mặt phẳng (ABC).

Tương tự, ta chứng minh được NP // BC, suy ra NP song song với mặt phẳng (ABC).

Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN và NP cùng song song với mặt phẳng (ABC) nên hai mặt phẳng (MNP) và (ABC) song song với nhau.

Bài 4.23 trang 94 Toán 11 Tập 1: Cho hình thang ABCD có hai đáy AB và CD. Qua các điểm A, D lần lượt vẽ các đường thẳng m, n song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh rằng mp(B, m) và mp(C, n) song song với nhau.

Lời giải:

Vì m // n nên đường thẳng m song song với mp(C, n).

Vì ABCD là hình thang có hai đáy là AB và CD nên AB // CD, suy ra đường thẳng AB song song với mp(C, n).

mp(B, m) chứa hai đường thẳng cắt nhau m và AB cùng song song với mp(C, n) nên mp(B, m) và mp(C, n) song song với nhau.

Bài 4.24 trang 94 Toán 11 Tập 1: Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm A₁, A₂ sao cho AA₁ = A₁A₂ = A₂S. Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua A₁, A₂. Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại B₁, C₁. Mặt phẳng (Q) cắt các cạnh SB, SC lần lượt tại B­₂, C₂. Chứng minh BB₁ = B₁B₂ = B₂S và CC₁ = C₁C₂ = C₂S.

Lời giải:

Vì hai mặt phẳng (P) và (Q) song song với mặt phẳng (ABC) nên (P) // (Q), do đó ba mặt phẳng (ABC), (P) và (Q) đôi một song song. Theo định lí Thalés trong không gian, ta suy ra $\frac{A_2{A}_1}{A{A}_1}=\frac{B_2{B}_1}{B{B}_1}=\frac{C_2{C}_1}{C{C}_1}$ .

Mà AA₁ = A₁A₂ nên $\frac{A_2{A}_1}{A{A}_1}=1$ , suy ra $\frac{A_2{A}_1}{A{A}_1}=\frac{B_2{B}_1}{B{B}_1}=\frac{C_2{C}_1}{C{C}_1}=1$ , do đó BB₁ = B₁B₂ và CC₁ = C₁C₂.

Sử dụng định lí Thalés ta cũng chứng minh được $\frac{A_{2}S}{A_2{A}_1}=\frac{B_{2}S}{B_2{B}_1}=\frac{C_{2}S}{C_2{C}_1}$ .

Mà A₁A₂ = A₂S nên $\frac{A_{2}S}{A_2{A}_1}=1$ , suy ra $\frac{A_{2}S}{A_2{A}_1}=\frac{B_{2}S}{B_2{B}_1}=\frac{C_{2}S}{C_2{C}_1}=1$ , do đó B₁B₂ = B₂S và C₁C₂ = C₂S.

Vậy BB₁ = B₁B₂ = B₂S và CC₁ = C₁C₂ = C₂S.

Bài 4.25 trang 94 Toán 11 Tập 1: Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Một mặt phẳng song song với mặt phẳng (A'B'C'D') cắt cạnh bên của hình lăng trụ lần lượt tại A", B", C", D". Hỏi hình tạo bởi các điểm A, B, C, D, A", B", C", D" là hình gì?

Lời giải:

Vì ABCD.A'B'C'D' là hình lăng trụ tứ giác nên hai mặt phẳng (ABCD) và (A'B'C'D') song song với nhau, mà mặt phẳng (A"B"C"D") song song với mặt phẳng (A'B'C'D'). Do đó, hai mặt phẳng (ABCD) và (A"B"C"D") song song với nhau (1).

Vì các cạnh bên của hình lăng trụ đôi một song song với nhau nên AA", BB", CC" đôi một song song (2).

Từ (1) và (2) suy ra ABCD.A"B"C"D" là hình lăng trụ tứ giác. Vậy hình tạo bởi các điểm A, B, C, D, A", B", C", D" là hình lăng trụ tứ giác.

Bài 4.26 trang 94 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G và G' lần lượt là trọng tâm của hai tam giác ABC và A'B'C'.

a) Chứng minh rằng tứ giác AGG'A' là hình bình hành.

b) Chứng minh rằng AGC.A'G'C' là hình lăng trụ.

Lời giải:

a) Gọi M và N lần lượt là trung điểm của BC và B'C'. Khi đó ta có MN là đường trung bình của hình bình hành BCC'B', suy ra MN // BB' và MN = BB'.

Do ABC.A'B'C' là hình lăng trụ tam giác nên AA' // BB' và AA' = BB'.

Từ đó suy ra MN // AA' và MN = AA'. Do đó, AMNA' là hình bình hành.

Suy ra AM // A'N và AM = A'N.

Vì G và G' lần lượt là trọng tâm của hai tam giác ABC và A'B'C' nên $\frac{A^{\text{'}}{G}^{\text{'}}}{A^{\text{'}}N}=\frac{AG}{AM}=\frac{2}{3}$ .

Do đó, AG = A'G' và AG // A'G'. Từ đó suy ra tứ giác AGG'A' là hình bình hành.

b) Vì tứ giác AGG'A' là hình bình hành nên AA' // GG'.

Tương tự ta chứng minh được CGG'C' là hình bình hành nên CC' // GG'.

Do đó, ba đường thẳng AA', GG' và CC' đôi một song song.

Lại có hai mặt phẳng (AGC) và (A'G'C') song song với nhau.

Vậy AGC.A'G'C' là hình lăng trụ tam giác.

Bài 4.27 trang 94 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Một mặt phẳng song song với mặt bên (ABB'A') của hình hộp và cắt các cạnh AD, BC, A'D', B'C' lần lượt tại M, N, M', N' (H.4.54). Chứng minh rằng ABNM.A'B'N'M' là hình hộp.

Lời giải:

Vì ABCD.A'B'C'D' là hình hộp nên các cạnh bên AA', BB', CC', DD' đôi một song song với nhau và (ABCD) // (A'B'C'D').

Vì M thuộc AD và N thuộc BC nên MN nằm trong mặt phẳng ABCD, tương tự M'N' nằm trong mặt phẳng (A'B'C'D'). Do đó, (ABNM) // (A'B'N'M') (1).

Ta có: (ABB'A') // (MNN'M') và mặt phẳng (ABCD) cắt (ABB'A') và (MNN'M') lần lượt theo các giao tuyến AB và MN, do đó AB // MN.

Tương tự, ta chứng minh được: M'N' // A'B'; NN' // BB'; MM' // AA'.

Mà AA' // BB' do đó bốn đường thẳng AA', BB', NN', MM' đôi một song song với nhau (2).

Từ (1) và (2) suy ra ABNM.A'B'N'M' là hình lăng trụ.

Tứ giác ABNM có AB // MN và AM // BN (do AD // BC) nên ABNM là hình bình hành.

Tứ giác A'B'N'M' có A'B' // M'N' và A'M' // B'N' (do A'D' // B'C') nên A'B'N'M' là hình bình hành.

Hình lăng trụ ABNM.A'B'N'M' có đáy là hình bình hành nên nó là hình hộp.

Bài 4.28 trang 94 Toán 11 Tập 1: Cầu thang xương cá là dạng cầu thang có hình dáng tương tự như những đốt xương cá, thường có những bậc cầu thang với khoảng mở lớn, tạo đượng sự nhẹ nhàng và thoáng đãng cho không gian sống. Trong Hình 4.55, phần mép của mỗi bậc thang nằm trên tường song song với nhau. Hãy giải thích tại sao.

Lời giải:

Các bậc cầu thang là các mặt phẳng song song với nhau từng đôi một, mặt phẳng tường cắt mỗi mặt phẳng là các bậc của cầu thang theo các giao tuyến là phần mép của mỗi bậc cầu thang nằm trên tường nên các giao tuyến này song song với nhau.

Video bài giảng Toán 11 Bài 13: Hai mặt phẳng song song - Kết nối tri thức

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Lý thuyết Hai mặt phẳng song song

1. Hai mặt phẳng song song

Hai mặt $\left(\alpha \right)$ và $\left(\beta \right)$ được gọi là song song với nhau nếu chúng không có điểm chung. Kí hiệu $\left(\alpha \right)$// $\left(\beta \right)$ hay $\left(\beta \right)$//$\left(\alpha \right)$.

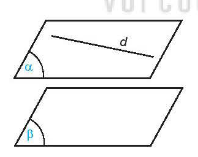
*Nhận xét: $\{\begin{array}{l}\left(\alpha \right)//\left(\beta \right)\\ d\subset \left(\alpha \right)\end{array}\Rightarrow d//\left(\beta \right)$.

2. Điều kiện và tính chất của hai mặt phẳng song song

Nếu mặt phẳng $\left(\alpha \right)$ chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng $\left(\beta \right)$thì $\left(\alpha \right)$và $\left(\beta \right)$song song với nhau.

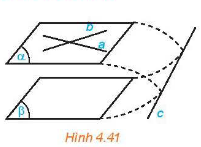
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

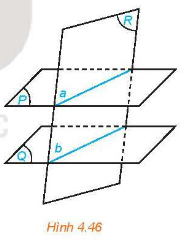
3. Định lí Thalès trong không gian

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.

$\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{BC}{B^{\prime }{C}^{\prime }}=\frac{AC}{A^{\prime }{C}^{\prime }}$

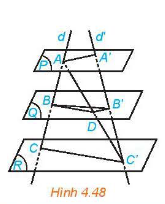
4. Hình lăng trụ và hình hộp

Cho hai mặt phẳng song song $\left(\alpha \right)$ và $\left({\alpha }^{\prime }\right)$. Trên $\left(\alpha \right)$ cho đa thức đa giác lồi $A_1{A}_2...A_n$. Qua các đỉnh$A_1,A_2,...,A_n$vẽ các đường thẳng đôi một song song và cắt mặt phẳng $\left({\alpha }^{\prime }\right)$tại ${A_1}^{\prime },{A_2}^{\prime },...,{A_n}^{\prime }$. Hình gồm hai đa giác$A_1{A}_2...A_n$, ${A_1}^{\prime }{A_2}^{\prime }...{A_n}^{\prime }$ và các tứ giác $A_1{A_1}^{\prime }{A_2}^{\prime }{A}_2$,$A_2{A_2}^{\prime }{A_3}^{\prime }{A}_3$,…,$A_n{A_n}^{\prime }{A_1}^{\prime }{A}_1$được gọi là hình lăng trụ và kí hiệu là $A_1{A}_2...A_n.{A_1}^{\prime }{A_2}^{\prime }...{A_n}^{\prime }$.

Các điểm $A_1,A_2,...,A_n$ và ${A_1}^{\prime },{A_2}^{\prime },...,{A_n}^{\prime }$được gọi là các đỉnh, các đoạn thẳng $A_1{A_1}^{\prime },A_2{A_2}^{\prime },...,A_n{A_n}^{\prime }$được gọi là các cạnh bên, các đoạn thẳng $A_1{A}_2,A_2{A}_3,...,A_n{A}_1$và ${A_1}^{\prime }{A_2}^{\prime },{A_2}^{\prime }{A_3}^{\prime },...,{A_n}^{\prime }{A_1}^{\prime }$ gọi là cạnh  đáy của hình trụ.

Hai đa giác $A_1{A}_2...A_n$và ${A_1}^{\prime }{A_2}^{\prime }...{A_n}^{\prime }$được gọi là hai mặt đáy của hình lăng trụ.

Các tứ giác $A_1{A_1}^{\prime }{A_2}^{\prime }{A}_2$,$A_2{A_2}^{\prime }{A_3}^{\prime }{A}_3$,…,$A_n{A_n}^{\prime }{A_1}^{\prime }{A}_1$ gọi là các mặt bên của hình trụ.

Hình lăng trụ tứ giác ABCD.A’B’C’D’ có hai đáy là hình bình hành được gọi là hình hộp.