Luyện tập 1 trang 89 Toán 11 Tập 1 Kết nối tri thức | Giải bài tập Toán lớp 11

Luyện tập 1 trang 89 Toán 11 Tập 1 Kết nối tri thức | Giải bài tập Toán lớp 11

Van Anh Ngày: 11-08-2024 Lớp 11

329

Với giải Luyện tập 1 trang 89 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 13: Hai mặt phẳng song song giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 13: Hai mặt phẳng song song

Luyện tập 1 trang 89 Toán 11 Tập 1: Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m, n lần lượt song song với hai đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD).

Lời giải:

Luyện tập 1 trang 89 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

Vì m // BC nên m // (BCD).

Vì n // BD nên n // (BCD).

mp(m, n) chứa hai đường thẳng cắt nhau m và n (cắt nhau tại A) cùng song song với mặt phẳng (BCD) nên mp(m, n) song song với mặt phẳng (BCD).

Lý thuyết Điều kiện và tính chất của hai mặt phẳng song song

Nếu mặt phẳng $(α)$ chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng $(β)$ thì $(α)$ và $(β)$ song song với nhau.

(ảnh 2)

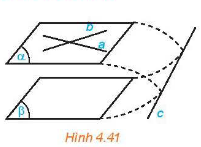
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

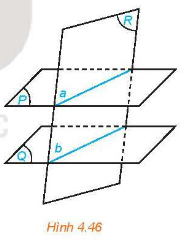
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

(ảnh 3)

Video bài giảng Toán 11 Bài 13: Hai mặt phẳng song song - Kết nối tri thức

Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Mở đầu trang 88 Toán 11 Tập 1: Các đầu bếp chuyên nghiệp luôn có kĩ năng dùng dao điêu luyện để thái thức ăn như rau, củ, thịt, cá,... thành các miếng đều nhau và đẹp mắt. Các nhát cắt cần tuân thủ nguyên tắc gì để đạt được điều đó?...

HĐ1 trang 88 Toán 11 Tập 1: Các mặt bậc thang trong Hình 4.40 gợi nên hình ảnh về các mặt phẳng không có điểm chung. Hãy tìm thêm một số ví dụ khác cũng gợi nên hình ảnh đó.....

Câu hỏi trang 88 Toán 11 Tập 1: Trong hình ảnh mở đầu, các nhát cắt có nằm trong các mặt phẳng song song hay kkhông....

HĐ2 trang 89 Toán 11 Tập 1: Cho mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) (H.4.41).....

Câu hỏi trang 89 Toán 11 Tập 1: Nếu không có điều kiện “hai đường thẳng cắt nhau” thì khẳng định trên còn đúng không?....

Luyện tập 1 trang 89 Toán 11 Tập 1: Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m, n lần lượt song song với hai đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD)......

Vận dụng 1 trang 89 Toán 11 Tập 1: Một chiếc bàn có phần chân là hai khung sắt hình chữ nhật có thể xoay quanh một trục như trong Hình 4.43. Khi mặt bàn được đặt lên phần chân bàn thì mặt bàn luôn song song với mặt đất. Hãy giải thích tại sao.....

HĐ3 trang 89 Toán 11 Tập 1: Đặt một tấm bìa cứng lên một góc của mặt bàn nằm ngang (H.4.44) sao cho mặt bìa song song với mặt đất. Khi đó mặt bìa có trùng bới mặt bàn hay không?...

Câu hỏi trang 89 Toán 11 Tập 1: Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì hai mặt phẳng đó có song song với nhau hay không? Vì sao?....

Luyện tập 2 trang 90 Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc cạnh SA, SB, SC, SD sao cho $\frac{M A}{M S} = \frac{N B}{N S} = \frac{P C}{P S} = \frac{Q D}{Q S} = \frac{1}{2}$ . Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng....

HĐ4 trang 90 Toán 11 Tập 1: Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46).....

Luyện tập 3 trang 91 Toán 11 Tập 1: Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).....

HĐ5 trang 91 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d' cắt ba mặt phẳng lần lượt tại A, B, C và A', B', C' (C khác C'). Gọi D là giao điểm của AC' và (Q) (H.4.48)....

Luyện tập 4 trang 91 Toán 11 Tập 1: Trong HĐ5, cho AB = 2 cm, BC = 4 cm và A'B' = 3 cm. Tính độ dài của đoạn thẳng B'C'.....

HĐ6 trang 91 Toán 11 Tập 1: Các hình ảnh dưới đây có đặc điểm chung nào với hình lăng trụ đứng tam giác mà em đã học ở lớp 7....

Câu hỏi trang 92 Toán 11 Tập 1: Hãy giải thích tại sao các mặt bên của hình lăng trụ là hình bình hành, từ đó suy ra các cạnh bên đôi một song song và có độ dài bằng nnhau...

Luyện tập 5 trang 92 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M và M' lần lượt là trung điểm của cạnh BC và B'C'. Chứng minh rằng AMC.A'M'C' là hình lăng trụ.....

HĐ7 trang 92 Toán 11 Tập 1: Hình ảnh nào trong HĐ6 gợi nên hình ảnh về hình lăng trụ có đáy là hình bình hành?...

Luyện tập 6 trang 93 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng hai mặt phẳng (ADD'A') và (BCC'B') song song với nhau....

Vận dụng 2 trang 93 Toán 11 Tập 1: Để xác định mực nước trong một chiếc bể có dạng hình hộp, bác Hà đặt một thanh gỗ đủ dài vào trong bể sao cho một đầu của thanh gỗ dựa vào mép của nắp bể, đầu còn lại nằm trên đáy bể (H.4.53). Sau đó bác Hà rút thanh gỗ ra ngoài và tính tỉ lệ giữa độ dài của phần thanh gỗ bị ngâm trong nước.. và độ dài của cả thanh gỗ. Tỉ lệ này chính bằng tỉ lệ giữa mực nước và chiều cao của bể. Hãy giải thích vì sao.....

Bài 4.21 trang 93 Toán 11 Tập 1: Trong không gian cho ba mặt phẳng phân biệt (P), (Q), (R). Những mệnh đề nào sau đây là đúng?....

Bài 4.22 trang 94 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AA', BB', CC'. Chứng minh rằng mặt phẳng (MNP) song song với mặt phẳng (ABC)....

Bài 4.23 trang 94 Toán 11 Tập 1: Cho hình thang ABCD có hai đáy AB và CD. Qua các điểm A, D lần lượt vẽ các đường thẳng m, n song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh rằng mp(B, m) và mp(C, n) song song với nhau.....

Bài 4.24 trang 94 Toán 11 Tập 1: Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm A₁, A₂ sao cho AA₁ = A₁A₂ = A₂S. Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua A₁, A₂. Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại B₁, C₁. Mặt phẳng (Q) cắt các cạnh SB, SC lần lượt tại B₂, C₂. Chứng minh BB₁ = B₁B₂ = B₂S và CC₁ = C₁C₂ = C₂S....

Bài 4.25 trang 94 Toán 11 Tập 1: Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Một mặt phẳng song song với mặt phẳng (A'B'C'D') cắt cạnh bên của hình lăng trụ lần lượt tại A", B", C", D". Hỏi hình tạo bởi các điểm A, B, C, D, A", B", C", D" là hình gì?....

Bài 4.26 trang 94 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G và G' lần lượt là trọng tâm của hai tam giác ABC và A'B'C'.....

Bài 4.27 trang 94 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Một mặt phẳng song song với mặt bên (ABB'A') của hình hộp và cắt các cạnh AD, BC, A'D', B'C' lần lượt tại M, N, M', N' (H.4.54). Chứng minh rằng ABNM.A'B'N'M' là hình hộp.....

Bài 4.28 trang 94 Toán 11 Tập 1: Cầu thang xương cá là dạng cầu thang có hình dáng tương tự như những đốt xương cá, thường có những bậc cầu thang với khoảng mở lớn, tạo đượng sự nhẹ nhàng và thoáng đãng cho không gian sống. Trong Hình 4.55, phần mép của mỗi bậc thang nằm trên tường song song với nhau. Hãy giải thích tại sao....

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Từ khóa :

Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

135

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.