Với giải HĐ3 trang 9 Toán 8 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Đơn thức và đa thức nhiều biến giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 1: Đơn thức và đa thức nhiều biến

Video bài giải Toán 8 Bài 1: Đơn thức và đa thức nhiều biến - Chân trời sáng tạo

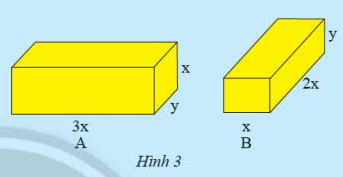
HĐ3 trang 9 Toán 8 Tập 1: Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3.

a) Tính tổng thể tích của hình hộp chữ nhật A và B.

b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.

Lời giải:

a) Thể tích của hình hộp chữ nhật A là: $V_A=3x.y.x=3.x^{2}y$

Thể tích của hình hộp chữ nhật B là: $V_B=2x.x.y=2x^{2}y$

Tổng thể tích của hình hộp chữ nhật A và B là: $3x^{2}y+2x^{2}y=\left(3+2\right).x^{2}y=5x^{2}y$

b) Biểu thức biểu diễn sự chênh lệch thể tích của A và B là: $3x^{2}y-2x^{2}y=\left(3-2\right).x^{2}y=x^{2}y$

Lý thuyết Đơn thức thu gọn

Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.

Thừa số là một số nói trên được gọi là hệ số, tích của các thừa số còn lại phần biến của đơn thức thu gọn.

Chú ý:

• Tổng số mũ của tất cả các biến có trong đơn thức (có hệ số khác 0) gọi là bậc của đơn thức đó.

• Ta coi một số khác 0 là đơn thức thu gọn, có hệ số bằng chính số đó và có bậc bằng 0.

• Đơn thức không (số 0) không có bậc.

• Khi viết đơn thức thu gọn ta thường viết hệ số trước, phần biến sau và các biến được viết theo thứ tự bảng chữ cái.

Ví dụ 3.Đơn thức nào sau đây là đơn thức thu gọn? Chỉ ra hệ số và bậc của mỗi đơn thức đó? Hãy thu gọn các đơn thức còn lại.

$-2\text{x}yz;\sqrt{10}{x}^{2}y{z}^3;3{\text{x}}^{2}yz.7yz;\frac{3}{4}$

Hướng dẫn giải

Các đơn thức thu gọn là

–2xyz, có hệ số là – 2, bậc bằng 1 + 1 + 1 = 3;

$\sqrt{10}{x}^{2}y{z}^3$, có hệ số là $\sqrt{10}$, bậc bằng 2 + 1 + 3 = 6;

$\frac{3}{4}$, có hệ số là $\frac{3}{4}$, bậc bằng 0

3x²yz . 7yz không phải là đơn thức thu gọn vì trong tích 3x²yz . 7yz có hai số là 3 và 7, các biến y, z xuất hiện hai lần

Thu gọn đơn thức:

3x²yz . 7yz = (3 . 7)x² (y . y)(z . z) = 21x²y²z².

Các đơn thức thu gọn là: $–2xyz;\sqrt{10}{x}^{2}y{z}^3;\frac{3}{4}$.

Đơn thức 3x²yz . 7yz không phải là đơn thức thu gọn vì trong tích 3x²yz . 7yz có hai số là 3 và 7; các biến y, z xuất hiện hai lần.

Thu gọn đơn thức:

3x²yz . 7yz = (3 . 7)x² (y . y)(z . z) = 21x²y²z².

Chú ý:

• Để thu gọn một đơn thức, ta nhóm các thừa số là các số rồi tính tích của chúng, nhóm các thừa số cùng một biến rồi viết tích của chúng thành lũy thừa của biến đó.

• Từ nay, khi nói đến đơn thức, nếu không nói gì thêm, ta hiểu đó là đơn thức thu gọn.