HĐ2 trang 61 Toán lớp 10: Trong Hình 4.33:
a) Hãy biểu thị mỗi vectơ →OM,→ON theo các vectơ →i,→j.
b) Hãy biểu thị vectơ →MN theo các vectơ →OM,→ON từ đó biểu thị vectơ →MN theo các vectơ →i,→j.
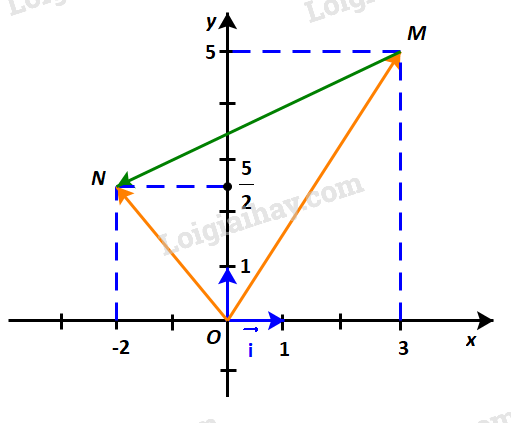
Phương pháp giải:
a) Quy tắc hình bình hành:
Tứ giác OAMB là hình bình hành thì →OM=→OA+→OB
b) Quy tắc hiệu: →MN=→ON−→OM
Lời giải:
Dựng hình bình hành OAMB và OCND như hình dưới:
Khi đó: →OM=→OA+→OB và →ON=→OC+→OD.
Dễ thấy:
→OA=3→i;→OB=5→j và →OC=−2→i;→OD=52→j
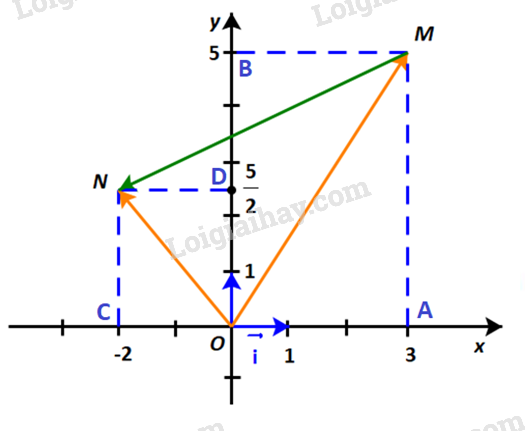
⇒{→OM=3→i+5→j→ON=−2→i+52→j
b) Ta có: →MN=→ON−→OM (quy tắc hiệu)
⇒→MN=(−2→i+52→j)−(3→i+5→j)⇔→MN=(−2→i−3→i)+(52→j−5→j)⇔→MN=−5→i−52→j
Vậy →MN=−5→i−52→j
Luyện tập 1 trang 61 Toán lớp 10: Tìm tọa độ của →0
Lời giải:
Vì: →0=0.→i+0.→j nên →0 có tọa độ là (0;0).
2. Biểu thức tọa độ của các phép toán vectơ
HĐ3 trang 61 Toán lớp 10: Trong mặt phẳng tọa độ Oxy, cho →u=(2;−3),→v=(4;1),→a=(8;−12)
a) Hãy biểu thị mỗi vectơ →u,→v,→a theo các vectơ →i,→j
b) Tìm tọa độ của các vectơ →u+→v,4.→u
c) Tìm mối liên hệ giữa hai vectơ →u,→a
Phương pháp giải:
a) Vectơ →a có tọa độ (x;y) thì →a=x.→i+y.→j
b)
Bước 1: Tính →u+→v,4.→u theo các vectơ →i,→j
Bước 2: Suy ra tọa độ của các vectơ →u+→v,4.→u
c)
Quan sát biểu thị theo các vectơ →i,→j của các vectơ →u,→a để suy ra mối liên hệ.
Lời giải:
a) Ta có: →u=(2;−3)
⇒→u=2.→i+(−3).→j
Tương tự ta có: →v=(4;1),→a=(8;−12)
⇒→v=4.→i+1.→j;→a=8.→i+(−12).→j
b) Ta có: {→u=2.→i+(−3).→j→v=4.→i+1.→j(theo câu a)
⇒{→u+→v=(2.→i+(−3).→j)+(4.→i+1.→j)4.→u=4(2.→i+(−3).→j)⇔{→u+→v=(2.→i+4.→i)+((−3).→j+1.→j)4.→u=4.2.→i+4.(−3).→j⇔{→u+→v=6.→i+(−2).→j4.→u=8.→i+(−12).→j
c) Vì {4.→u=8.→i+(−12).→j→a=8.→i+(−12).→j nên ta suy ra 4.→u=→a
Xem thêm lời giải Toán 10 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
