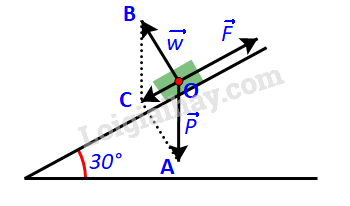
Vận dụng trang 54 Toán lớp 10: Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148 N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng so với phương nằm ngang (H.4.18). Nếu lực kéo của mỗi người bằng 100N, thì cần tối thiểu bao nhiêu người để kéo pháo?
Phương pháp giải:
Khi cân bằng lực (trọng lực, phản lực, lực kéo) thì khẩu pháo đứng yên, do đó để kéo được khẩu pháo lên thì lực kéo phải lớn hơn hoặc bằng tổng hợp lực của trọng lực và phản lực.
Tìm hướng và độ lớn của tổng hợp lực giữa trọng lực và phản lực, từ đó suy ra độ lớn của lực kéo.
Lời giải:
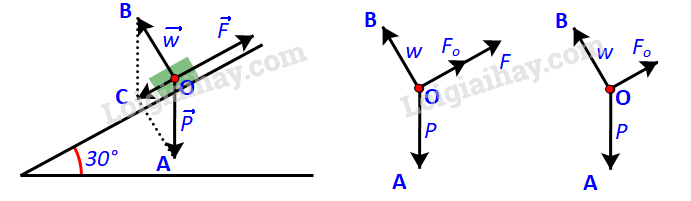
Khẩu pháo chịu tác động của ba lực: trọng lực (kí hiệu ), phản lực (kí hiệu ) và lực kéo . Để kéo pháo thì độ lớn của lực kéo phải lớn hơn độ lớn của lực kéo khi pháo cân bằng (kí hiệu )
Khi pháo cân bằng thì:
Để tổng hợp lực và , ta vẽ hình bình hành OACB.
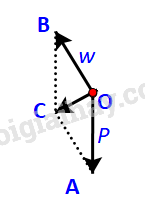
Ta có:
là trung điểm của , hay .
Lại có: (do là phản lực)
Mà ;
Vậy lực có độ lớn là , để kéo pháo thì lực cùng hướng với và
Vì nên cần tối thiểu 111 người để kéo pháo.
Bài tập
Bài 4.6 trang 54 Toán lớp 10: Cho bốn điểm . Chứng minh rằng:
a)
b)
Phương pháp giải:
Với 3 điểm A, B, C bất kì, ta có: và
Lời giải:
a)
b)
và
Bài 4.7 trang 54 Toán lớp 10: Cho hình bình hành ABCD. Hãy tìm điểm M để . Tìm mối quan hệ giữa hai vectơ và .
Phương pháp giải:
Bước 1: Xác định vectơ dựa vào quy tắc hình bình hành, từ đó xác định điểm M.
Bước 2: Nhận xét về phương và chiều của hai vectơ và hoặc tìm biểu thức liên hệ giữa hai vectơ đó.
Lời giải:
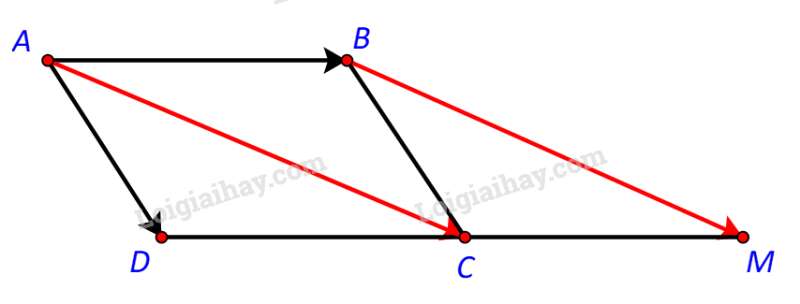
Ta có: (do ABCD là hình bình hành)
Tứ giác ABMC là hình bình hành.
. Mà
là trung điểm DM.
Nói cách khác: hay hai vectơ và đối nhau.
Chú ý khi giải
+) Tứ giác ABCD là hình bình hành
+) ABCD là hình bình hành thì
Bài 4.8 trang 54 Toán lớp 10: Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của các vectơ
Phương pháp giải:
Với 3 điểm A, B, C bất kì, ta có:
Tứ giác MNPQ là hình bình hành thì
Lời giải:
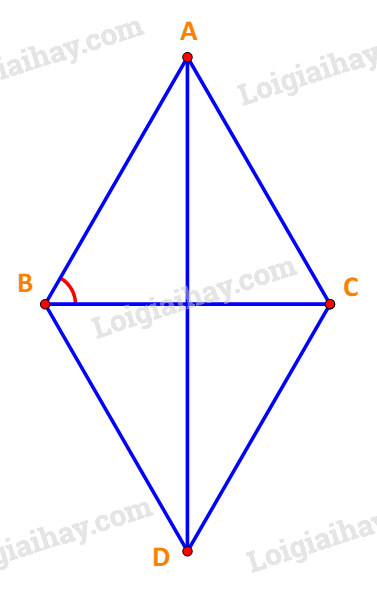
Dựng hình bình hành ABDC tâm O như hình vẽ.
Ta có:
Vì tứ giác ABDC là hình bình hành, lại có nên ABDC là hình thoi.
Vậy và .
Bài 4.9 trang 54 Toán lớp 10: Hình 4.19 biểu diễn hai lực cùng tác động lên một vật, cho Tính độ lớn của hợp lực .
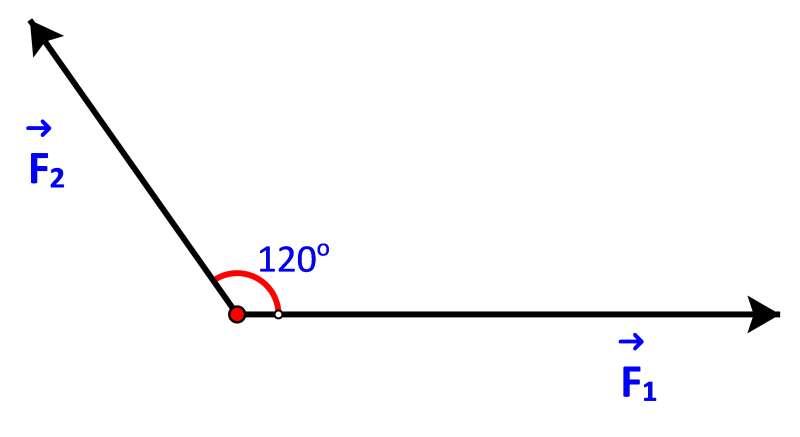
Phương pháp giải:
Để tìm tổng của hai vectơ chung gốc ta dựng hình hình bành ABDC, khi đó:
Lời giải:
Dựng hình bình hành ABDC với hai cạnh là hai vectơ như hình vẽ
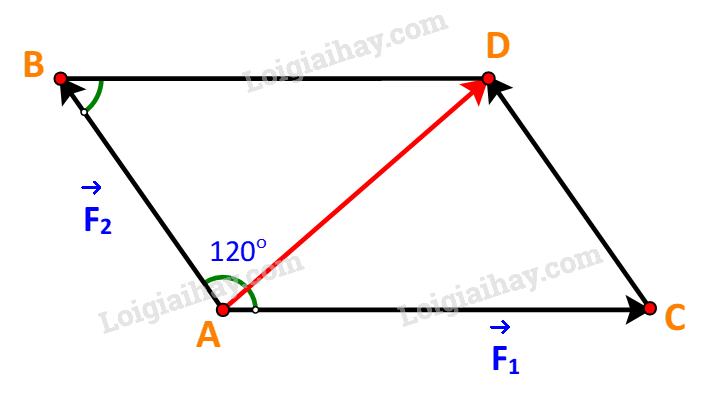
Ta có:
Xét ta có:
Theo định lí cosin ta có:
Vậy
Bài 4.10 trang 54 Toán lớp 10: Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không khổi và có độ lớn bàng nhau. Hai tàu luôn dược giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yêu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước.
Phương pháp giải:
Biểu diễn hướng đi của hai tàu.
Phân tích theo vectơ vận tốc riêng và vận tốc dòng nước.
Lời giải:
Ta đã biết vectơ dòng nước và hướng di chuyển (tức là vectơ vận tốc thực của hai tàu).
Ta cần xác định vectơ vận tốc của mỗi tàu, chỉ biết chúng có độ lớn bằng nhau.
Giả sử tàu 1 là tàu đi về phía hạ lưu còn tàu 2 là tàu đi về phía thượng nguồn.
Tàu 1 và tàu 2 bắt đầu di chuyển từ điểm A và A’ ở bờ bên này đến điểm E, E’ ở bờ bên kia.
Vecto vận tốc dòng nước tác động lên tàu là như nhau, biểu diễn bởi các vectơ và
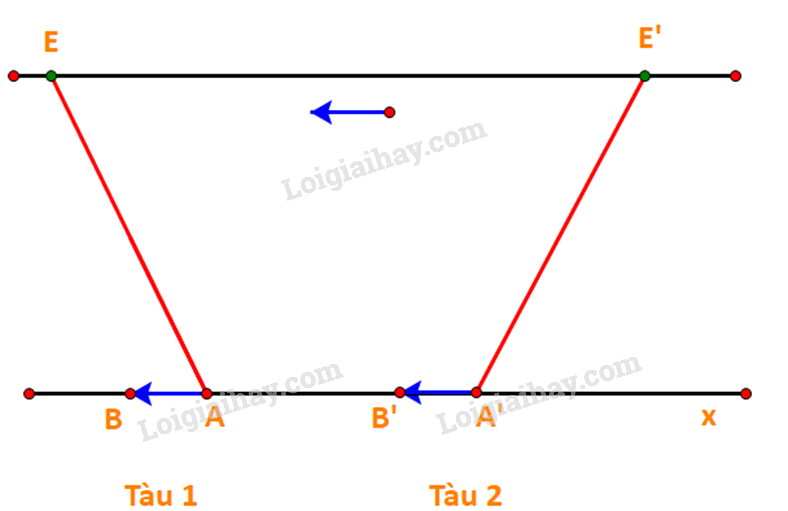
Gọi vectơ vận tốc riêng của hai tàu lần lượt là các vectơ và
Vecto vận tốc thực của hai tàu là vectơ và .
Với tàu 1, để xác định các điểm C, D:
Từ B ta kẻ đường vuông góc với bờ, cắt AE tại một điểm, kí hiệu là C. Tiếp theo, dựng hình bình hành ABCD ta được điểm D.
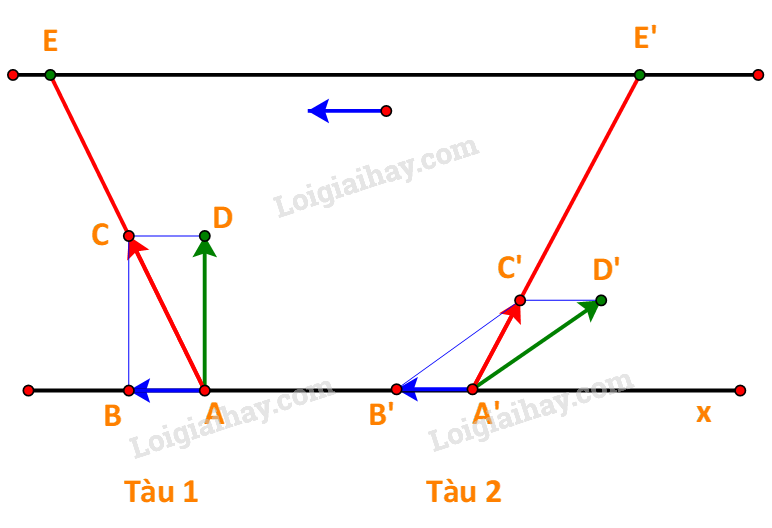
Với tàu 2, để xác định các điểm C’, D’
Trên A’E’ lấy điểm C’ sao cho B’C’= AD. Dựng hình bình hành A’B’C’D’, ta được điểm D’.
Giải thích:
Tàu 1: Được dòng nước đẩy theo vectơ , và đi với vận tốc thực là vectơ , khi ấy hướng di chuyển là vectơ tổng chính là vectơ
Tàu 2: Bị dòng nước đẩy theo vectơ , và đi với vận tốc thực là vectơ , khi ấy hướng di chuyển là vectơ tổng chính là vectơ
Các vectơ và có độ dài bằng nhau (cùng bằng B’C’).
Do hai tàu chuyển động theo hướng tạo với bờ cùng một góc nhọn nên quãng đường đường đi khi chạm bờ bên kia là như nhau. Hay AE = A’E’.
Tàu nào có độ lớn vận tốc thực lớn hơn thì tàu đó sang bờ bên kia trước.
Xét tam giác A’B’C’, theo định lí cosin ta có:
Mà
Mặt khác, tam giác ABC vuông tại B nên:
hay
Vậy vận tốc của tàu 1 lớn hơn, nói cách khác tàu đi hướng xuống hạ lưu sẽ sang bờ bên kia trước.
Xem thêm lời giải Toán 10 Kết nối tri thức hay, chi tiết khác: