Hoạt động 3 trang 38 Toán 10 Tập 2 | Kết nối tri thức Giải Toán lớp 10

Hoạt động 3 trang 38 Toán 10 Tập 2 | Kết nối tri thức Giải Toán lớp 10

Hoàng Ngân Ngày: 28-03-2023 Lớp 10

832

Với giải Hoạt động 3 trang 38 SGK Toán 10 Kết nối tri thức chi tiết trong Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

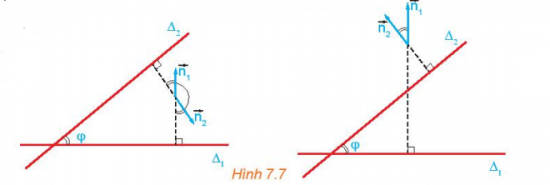
Hoạt động 3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆1 và ∆2 tương ứng có các vectơ pháp tuyến $\vec{n_{1}}; \vec{n_{2}}$ . Gọi φ là góc giữa hai đường thẳng đó (H7.7). Nêu mối quan hệ giữa:

a) góc φ và góc ( $\vec{n_{1}}; \vec{n_{2}}$ );

b) cos φ và cos( $\vec{n_{1}}; \vec{n_{2}}$ ).

Giải Toán 10 Bài 20 (Kết nối tri thức): Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. (ảnh 1)

Lời giải:

a)

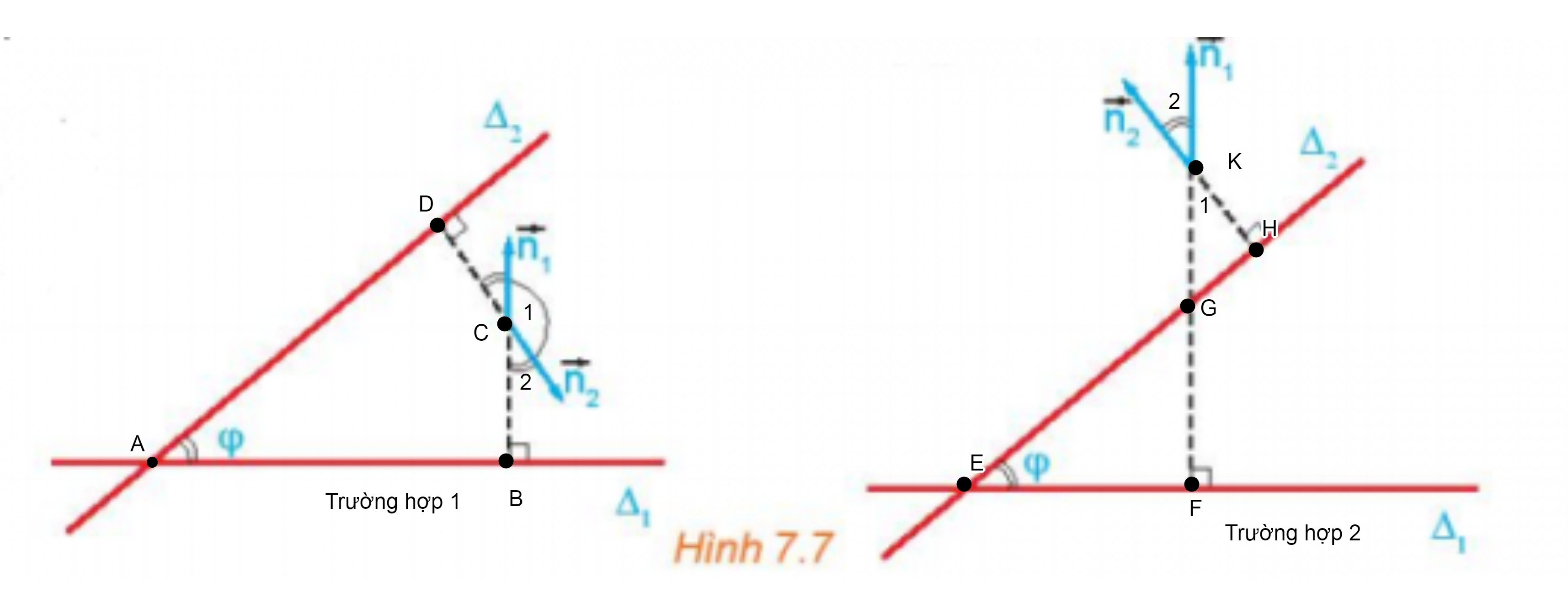
Giải Toán 10 Bài 20 (Kết nối tri thức): Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. (ảnh 1)

* Xét trường hợp 1:

Xét tứ giác ABCD có hai góc $\hat{A D C;} \hat{C B A}$ bằng 900 nên tứ giác ABCD là tứ giác nội tiếp.

Theo tính chất góc ngoài của tứ giác nội tiếp ta có : $\hat{A} = \hat{C_{2}}$ = φ

Mặt khác ta có: $\hat{C_{2}}$ và $(\vec{n_{1}}; \vec{n_{2}})$ là hai góc kề bù nên $(\vec{n_{1}}; \vec{n_{2}})$ = 180°– $\hat{C_{2}}$ = 180° – φ hay $(\vec{n_{1}}; \vec{n_{2}})$ + φ = 180°

⇒ $(\vec{n_{1}}; \vec{n_{2}})$ và φ là hai góc bù nhau. (1)

* Xét trường hợp 2:

Chứng minh tương tự ta có tứ giác EFHK là tứ giác nội tiếp

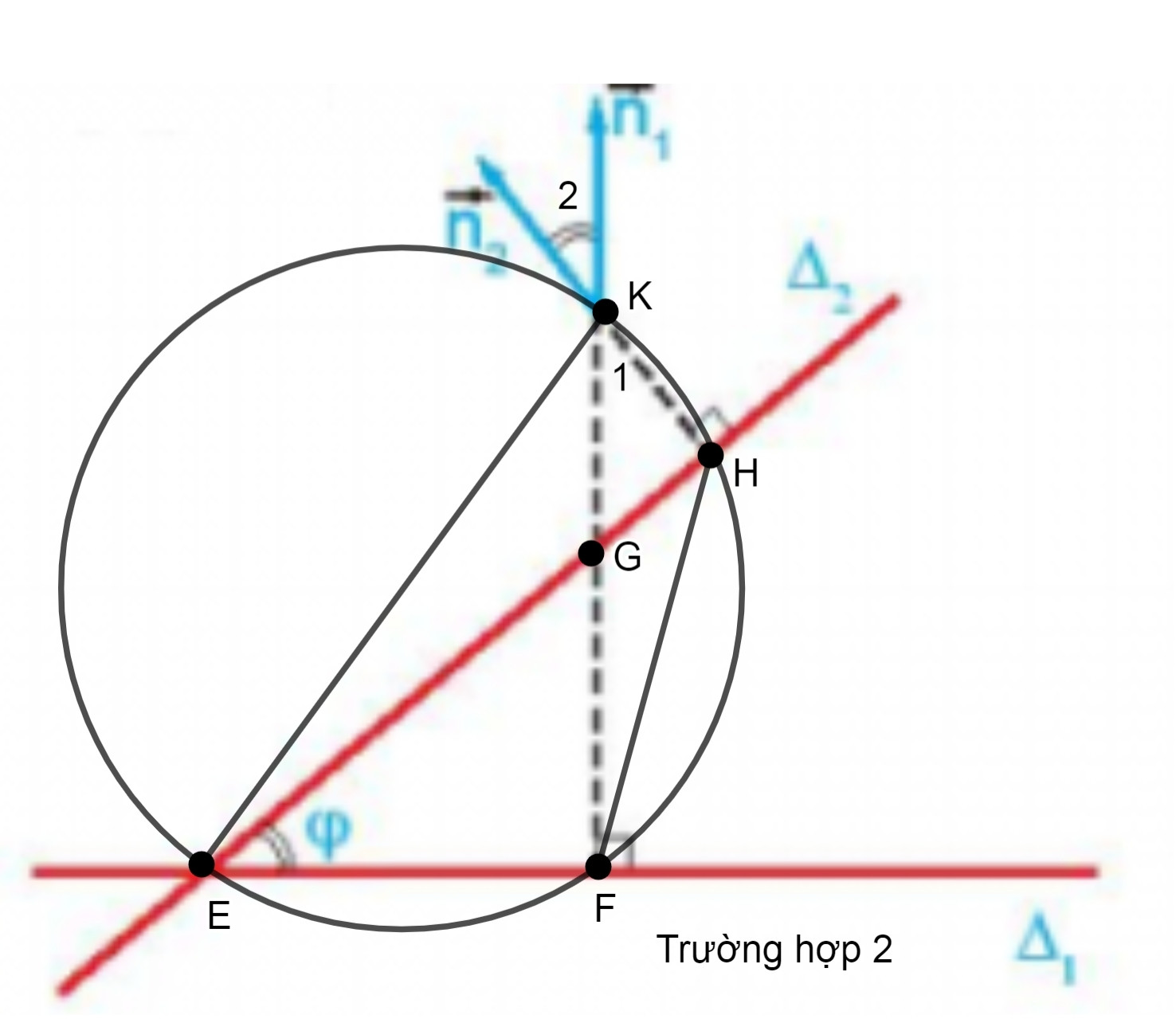
Giải Toán 10 Bài 20 (Kết nối tri thức): Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. (ảnh 1)

Ta có: $\hat{F E H}$ = $\hat{K_{1}}$ = φ (Vì hai góc nội tiếp $\hat{F E H}$ và $\hat{K_{1}}$ cùng chắn cung FH)

Mặt khác ta có: $\hat{K_{1}}$ và $(\vec{n_{1}}; \vec{n_{2}})$ là hai góc đối đỉnh nên $\hat{K_{1}}$ = $(\vec{n_{1}}; \vec{n_{2}})$

⇒ $(\vec{n_{1}}; \vec{n_{2}})$ = φ. (2)

Từ (1) và (2) suy ra: $(\vec{n_{1}}; \vec{n_{2}})$ = φ hoặc $(\vec{n_{1}}; \vec{n_{2}})$ + φ = 180°.

Vậy mối quan hệ giữa góc $(\vec{n_{1}}; \vec{n_{2}})$ và góc φ là $(\vec{n_{1}}; \vec{n_{2}})$ = φ hoặc $(\vec{n_{1}}; \vec{n_{2}})$ + φ = 180°.

b)

* Xét trường hợp 1: $(\vec{n_{1}}; \vec{n_{2}})$ = 180° – φ

Do đó cos $(\vec{n_{1}}; \vec{n_{2}})$ = cos(180° – φ) = -cos φ

* Xét trường hợp 2 : $(\vec{n_{1}}; \vec{n_{2}})$ = φ

Ta có: cos $(\vec{n_{1}}; \vec{n_{2}})$ = cosφ.

Vậy cos $(\vec{n_{1}}; \vec{n_{2}})$ = |cosφ|.

Xem thêm lời giải sách giáo khoa Toán 10 Kết nối tri thức hay, chi tiết khác:

Hoạt động 1 trang 36 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho hai đường thẳng...

Luyện tập 1 trang 37 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau:...

Hoạt động 2 trang 37 Toán 10 Tập 2: Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mỗi quan hệ gì với nhau?...

Hoạt động 3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆1 và ∆2 tương ứng có các vectơ pháp tuyến $\vec{n_{1}}; \vec{n_{2}}$ . Gọi φ là góc giữa hai đường thẳng đó (H7.7). Nêu mối quan hệ giữa:...

Luyện tập 2 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1: x + 3y + 2 = 0 và $∆$ 2: y = 3x + 1...

Luyện tập 3 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1: $\{\begin{cases} x = 2 + t \\ y = 1 - 2 t \end{cases}$ và ∆2: $\{\begin{cases} x = 1 + t' \\ y = 5 + 3 t' \end{cases}$ ...

Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0...

Hoạt động 4 trang 40 Toán 10 Tập 2: Cho điểm M(x0; y0) và đường thẳng ∆ : ax + by + c = 0 có vectơ pháp tuyến $\vec{n}$ (a; b). Gọi H là hình chiếu vuông góc của M lên ∆ (H.7.9)...

Trải nghiệm trang 40 Toán 10 Tập 2: Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4...

Luyện tập 5 trang 40 Toán 10 Tập 2: Tính khoảng cách từ điểm M(1; 2) đến đường thẳng ∆: $\{\begin{cases} x = 5 + 3 t \\ y = - 5 - 4 t \end{cases}$ ...

Vận dụng trang 41 Toán 10 Tập 2: Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15m, chiều rộng AB = 12m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5m, CF = 6m (H.7.11)...

Bài 7.7 trang 41 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau:..

Bài 7.8 trang 41 Toán 10 Tập 2: Tính góc giữa các cặp đường thẳng sau:...

Bài 7.9 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ Oxy cho điểm A(0; –2) và đường thẳng ∆ : x + y – 4 = 0...

Bài 7.10 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(–2; –1)...

Bài 7.11 trang 42 Toán 10 Tập 2: Chứng minh hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) vuông góc với nhau khi và chỉ khi aa’ = –1...

Bài 7.12 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại 3 vị trí O(0; 0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh...

Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 19: Phương trình đường thẳng

Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 22: Ba đường Conic

Bài tập cuối chương 7

Từ khóa :

toán 10 Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

170

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

117

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.