Luyện tập 2 trang 15 Toán lớp 10: Giả sử C là tập hợp các hình bình hành có hai đường chéo vuông góc; D là tập hợp các hình vuông.

Các mệnh đề sau đúng hay sai?

a) $C\subset D$;

b) $C\supset D$;

c) $C=D$.

Phương pháp giải:

Mô tả tập hợp C và tập hợp D.

So sánh các phần tử của hai tập hợp.

Lời giải:

+) Mô tả tập hợp D = {các hình vuông}

+) Mô tả tập hợp C = {các hình bình hành có hai đường chéo vuông góc} = {Các hình thoi}.

Thật vậy,

Xét tứ giác ABCD, là hình hình hành có hai đường chéo vuông góc.

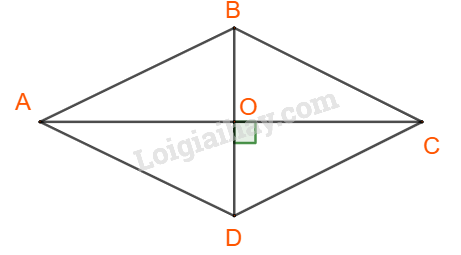
Gọi $AC\cap BD=O$ thì O là trung điểm của AC và BD.

Ta có: AO vừa là trung tuyến vừa là đường cao.

$\Rightarrow \mathrm{\Delta }ABD$ cân tại A.

$\Rightarrow AB=AD$.

Tương tự ta cũng có: $CB=CD$.

Mà $AB=CD;AD=BC$.

Do đó: $AB=CD=AD=BC$ hay tứ giác ABCD là hình thoi.

a) Vì nhiều hình thoi (các hình thoi không có góc nào vuông) thì không phải là hình vuông, nên $C\text{⧸}\subset D$.

Vậy mệnh đề “$C\subset D$” sai.

b) Vì mỗi hình vuông cũng là một hình thoi (hình thoi đặc biệt: có một góc vuông), nên các phần tử của D cũng là phần tử của D. Hay $C\supset D$
Do đó mệnh đề “$C\supset D$” đúng.

c) Vì $\{\begin{array}{l}C\subset D\\ C\supset D\end{array}\Rightarrow C\ne D$

Vậy mệnh đề “$C=D$” sai.

2. Các tập hợp số

HĐ5 trang 15 Toán lớp 10:  Các mệnh đề sau đúng hay sai?

a) Mọi số nguyên đều viết được dưới dạng phân số

b) Tập hợp các số thực chứa tập hợp các số hữu tỉ;

c) Tồn tại một số thực không là số hữu tỉ.

Phương pháp giải:

Nhắc lại: $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}$

Lời giải:

a) Dễ thấy: $\mathrm{\forall }a\in \mathbb{Z}:a={\displaystyle \frac{a}{1}}$

Vậy mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.

Hoặc:

Ta có; $\mathbb{Z}\subset \mathbb{Q}$ hay mỗi số nguyên cũng là một phân số.

Do đó mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.

b) Mệnh đề viết dưới dạng kí hiệu: “$\mathbb{R}\supset \mathbb{Q}$”, là mệnh đề đúng.

c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.

Ví dụ: $\sqrt{2}$ ( vì $\sqrt{2}\in \mathbb{R};\sqrt{2}\notin \mathbb{Q}$).

Luyện tập 3 trang 15 Toán lớp 10: Cho tập hợp C = {-4; 0; 1; 2}. Các mệnh đề sau đúng hay sai?

a) C là tập con của $\mathbb{Z}$

b) C là tập con của $\mathbb{N}$

c) C là tập con của $\mathbb{R}$

Phương pháp giải:

C là tập con của X nếu mỗi phần tử của C đều là phần tử của X.

Lời giải:

a) Dễ thấy: $-4;0;1;2\in \mathbb{Z}$

Vậy C là tập con của $\mathbb{Z}$, mệnh đề đúng.

b) Vì $-4\notin \mathbb{N}$ nên C không là tập con của $\mathbb{N}$

Vậy mệnh đề sai.

c) Dễ thấy: $-4;0;1;2\in \mathbb{R}$

Vậy C là tập con của $\mathbb{R}$, mệnh đề đúng.

Xem thêm lời giải Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải Toán 10 trang 12 Tập 1

Giải Toán 10 trang 13 Tập 1 

Giải Toán 10 trang 14 Tập 1 

Giải Toán 10 trang 15 Tập 1 

Giải Toán 10 trang 16 Tập 1 

Giải Toán 10 trang 17 Tập 1 

Giải Toán 10 trang 18 Tập 1 

Giải Toán 10 trang 19 Tập 1