Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Ôn tập chương 3: Hệ hai phương trình bậc nhất hai ẩn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Ôn tập chương 3: Hệ hai phương trình bậc nhất hai ẩn
a)
b)
c)
d)
Phương pháp giải:
Sử dụng: Cách giải hệ phương trình bằng phương pháp thế hoặc cộng đại số
Lời giải:
a)
Vậy hệ phương trình đã cho có nghiệm duy nhất là
b)
Vậy hệ phương trình đã cho có nghiệm duy nhất là
c)
Vậy hệ phương trình đã cho có nghiệm duy nhất là
d)
Vậy hệ phương trình đã cho có nghiệm duy nhất là
a)
b)
Phương pháp giải:
Cách giải hệ phương trình bằng phương pháp cộng đại số:
+ Bước : Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.
+ Bước : Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
+ Bước : Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Lời giải:
a)
Vậy hệ phương trình đã cho có nghiệm duy nhất là
b)
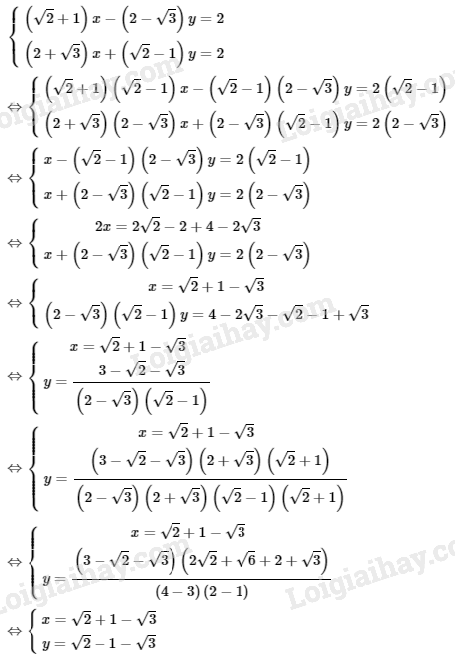
Vậy hệ phương trình đã cho có nghiệm duy nhất là
có nghiệm là
Phương pháp giải:
Sử dụng:
- Cặp số là nghiệm của hệ phương trình
Lời giải:
Cặp là nghiệm của hệ phương trình nên thay vào hệ đã cho, ta có:
Vậy
Phương pháp giải:
Sử dụng:
- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :
Bước : Lập hệ phương trình
+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng
+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước : Giải hệ phương trình nói trên.
Bước : Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
- Nếu chia được thương là , số dư là thì ta có biểu diễn:
Lời giải:
Gọi chữ số hàng chục là , chữ số hàng đơn vị là .
Điều kiện:
Hai lần chữ số hàng chục lớn hơn năm lần chữ số hàng đơn vị là nên ta có phương trình:
Chữ số hàng chục chia cho chữ số hàng đơn vị được thương là và dư là nên ta có phương trình:
Khi đó ta có hệ phương trình:
Ta thấy thỏa mãn điều kiện bài toán.
Vậy số cần tìm là .
Phương pháp giải:
Sử dụng:
- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :
Bước : Lập hệ phương trình
+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng
+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước : Giải hệ phương trình nói trên.
Bước : Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải:
Gọi số hàng cần chuyển là (tấn), số toa để chở là (toa).
Điều kiện: và
Nếu xếp vào mỗi toa tấn hàng thì còn thừa lại tấn, khi đó ta có phương trình:
Nếu xếp vào mỗi toa tấn thì còn có thể chở thêm tấn nữa, khi đó ta có phương trình:
Ta có hệ phương trình:
Giá trị thỏa mãn điều kiện bài toán.
Vậy xe lửa có toa và phải chở tấn.
Phương pháp giải:
Sử dụng:
- Xem toàn bộ công việc là (công việc)
- Thực hiện một công việc trong ngày thì xong việc.
Suy ra trong một ngày thực hiện được công việc
- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :
Bước : Lập hệ phương trình
+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng
+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước : Giải hệ phương trình nói trên (sử dụng phương pháp đặt ẩn số phụ)
Bước : Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải:
Gọi thời gian đội thứ nhất làm một mình xong công việc là (ngày), thời gian đội thứ hai làm một mình xong công việc là (ngày)
Điều kiện:
Trong ngày đội thứ nhất làm được (công việc)
Trong ngày đội thứ hai làm được (công việc)
Hai đội cùng làm thì trong ngày xong việc, khi đó trong ngày cả hai đội làm được (công việc)
Ta có phương trình:
Hai đội cùng làm trong ngày, sau đó đội thứ nhất làm tiếp một mình trong ngày nữa thì xong công việc, ta có phương trình:
Ta có hệ phương trình:
Đặt ta có:
Suy ra:
Giá trị thỏa mãn điều kiện bài toán.
Vậy đội thứ nhất làm một mình trong ngày thì xong công việc, đội thứ hai làm một mình trong ngày thì xong công việc.
Phương pháp giải:
Sử dụng:
- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :
Bước : Lập hệ phương trình
+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng
+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước : Giải hệ phương trình nói trên.
Bước : Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
- Công thức tính quãng đường đi được:
Trong đó là quãng đường đi được ; là vận tốc ; là thời gian .
Lời giải:
Gọi vận tốc của xe thứ nhất là , vận tốc của xe thứ hai là
Điều kiện:
Hai xe khởi hành cùng một lúc và đi ngược chiều nhau thì sau giờ gặp nhau nên tổng quãng đường hai xe đi được là 750km, ta có phương trình:
Xe thứ nhất khởi hành trước xe thứ hai giờ phút thì sau khi xe thứ hai đi được giờ chúng gặp nhau. Như vậy thời gian xe thứ nhất đi là:
giờ phút giờ.
Khi đó ta có phương trình:
Ta có hệ phương trình:
Ta thấy thỏa mãn điều kiện bài toán.
Vậy vận tốc của xe thứ nhất là ; vận tốc của xe thứ hai là
Bài tập bổ sung (trang 16 SBT Toán 9)
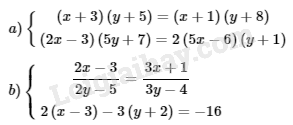
Phương pháp giải:
Sử dụng:
- Biến đổi hệ phương trình đã cho về hệ hai phương trình bậc nhất hai ẩn.
- Cách giải hệ phương trình bằng phương pháp cộng đại số:
+ Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.
+ Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
+ Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Lời giải :
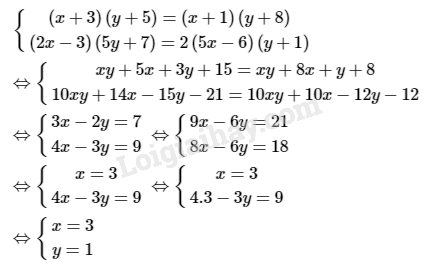
Vậy hệ phương trình đã cho có nghiệm duy nhất là .
Điều kiện:
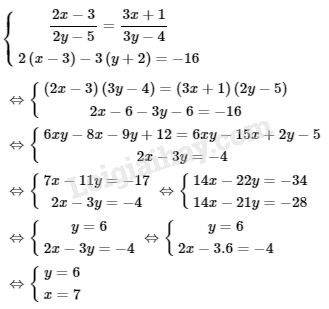
Ta thấy thoả mãn điều kiện bài toán.
Vậy hệ phương trình đã cho có nghiệm duy nhất là .
Phương pháp giải:
Sử dụng:
- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :
Bước 1: Lập hệ phương trình
+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng
+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải hệ phương trình nói trên.
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải:
Gọi khối lượng lúa thu được năm ngoái trên cánh đồng thứ nhất và cánh đồng thứ hai lần lượt là (tấn), (tấn).
Điều kiện:
Năm ngoái trên cả hai cánh đồng lượng lúa thu được là tấn, ta có phương trình:
Lượng lúa thu được năm nay trên cánh đồng thứ nhất tăng lên 30% so với năm ngoái tức là tăng (tấn)
Lượng lúa thu được năm nay trên cánh đồng thứ hai tăng lên 20% so với năm ngoái tức là tăng (tấn)
Năm nay lượng lúa trên cả hai cánh đồng tăng được tấn, ta có phương trình:
Ta có hệ phương trình:
Giá trị thỏa mãn điều kiện bài toán.
Vậy năm nay trên cánh đồng thứ nhất thu được: tấn.
Năm nay trên cánh đồng thứ hai thu được: tấn.
Phương pháp giải:
Sử dụng:
- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :
Bước 1: Lập hệ phương trình
+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng
+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải hệ phương trình nói trên.
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải:
Gọi khối lượng quặng loại thứ nhất là (tấn), loại thứ hai là (tấn).
Điều kiện:
Lượng sắt nguyên chất có trong mỗi loại quặng bằng lượng sắt có trong hỗn hợp nên ta có phương trình:
Nếu tăng khối lượng của mỗi loại quặng thêm tấn thì được một loại quặng chứa 63,25% sắt, khi đó ta có phương trình:
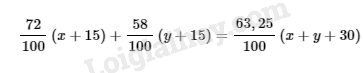
Ta có hệ phương trình:

Cả hai giá trị thỏa mãn điều kiện bài toán.
Vậy khối lượng quặng loại thứ nhất là tấn, loại thứ hai là tấn.
Bài III.4 trang 16 SBT Toán 9 tập 2: Một người đi ngựa và một người đi bộ đều đi từ bản đến bản . Người đi ngựa đến trước người đi bộ phút rồi lập tức quay trở về và gặp người đi bộ tại một địa điểm cách là . Trên cả quãng đường từ đến và ngược lại, người đi ngựa đi hết giờ phút. Hãy tính khoảng cách và vận tốc của mỗi người.Phương pháp giải:
Sử dụng:
- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :
Bước : Lập hệ phương trình
+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng
+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước : Giải hệ phương trình nói trên.
Bước : Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
- Công thức tính quãng đường đi được:
Trong đó là quãng đường đi được ; là vận tốc ; là thời gian .
Lời giải:
Gọi khoảng cách giữa hai bản và là , vận tốc của người đi bộ là .
Điều kiện:
Đổi giờ phút giờ
Người đi ngựa đi từ đến và ngược lại hết nên người đi ngựa đi từ đến hết .
Vận tốc của người đi ngựa là
Thời gian người đi bộ đi hết quãng đường là
Người đi ngựa đến trước người đi bộ phút tức là giờ, ta có phương trình:
Từ suy ra Điều này có nghĩa là vận tốc của người đi ngựa gấp đôi vận tốc của người đi bộ hay vận tốc của người đi ngựa là
Từ lúc đi đến lúc gặp nhau người đi bộ đi được , người đi ngựa đi được
Vì từ lúc đi đến lúc gặp nhau thời gian hai người đi bằng nhau nên ta có phương trình:
Ta có hệ phương trình:
Ta thấy và thỏa mãn điều kiện bài toán.
Vậy khoảng cách là , vận tốc của người đi bộ là , vận tốc của người đi ngựa là .