Giải Toán 7 trang 67 Tập 1 Kết nối tri thức

ndiep Ngày: 29-12-2022 Lớp 7

384

Với Giải toán lớp 7 trang 67 Tập 1 Kết nối tri thức chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 67 Tập 1 Kết nối tri thức

Vận dụng trang 67 Toán lớp 7: Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy

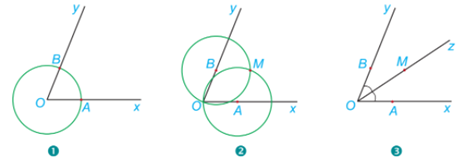
1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.

2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.

3. Vē tia Oz đi qua M.

Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.

Phương pháp giải:

Chứng minh hai tam giác $Δ O B M$ và $Δ O A M$ bằng nhau

Từ đó suy ra OM là tia phân giác của góc xOy.

Lời giải:

Xét $Δ O B M$ và $Δ O A M$ có:

$O A = O B (= R)$

OM chung

AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)

$\Rightarrow$ $Δ O B M$ = $Δ O A M$ (c.c.c)

$\Rightarrow$ $\hat{M O B} = \hat{M O A}$ (hai góc tương ứng)

Mà tia OM nằm trong góc xOy

Vậy OM là tia phân giác của góc xOy.

Bài tập

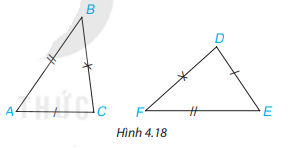
Bài 4.4 trang 67 Toán lớp 7: Cho tam giác ABC và DEF như hình 4.18. Trong các khẳng định sau, khẳng định nào đúng?

(1) $Δ A B C = Δ D E F$

(2) $Δ A C B = Δ E D F$

(3) $Δ B A C = Δ D F E$

(4) $Δ C A B = Δ D E F$

Phương pháp giải:

Quan sát hình vẽ chỉ ra các cặp cạnh bằng nhau từ đó suy ra thứ tự đỉnh của hai tam giác bằng nhau.

Lời giải:

Xét tam giác $Δ A C B$ và $Δ E D F$ có:

$\begin{array}{l} A C = E D \\ A B = E F \\ C B = D F \end{array}$

Suy ra $Δ A C B = Δ E D F$ (c.c.c)

Vậy khẳng định (2) đúng.

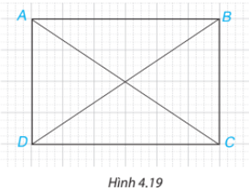
Bài 4.5 trang 67 Toán lớp 7: Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.

Phương pháp giải:

Chỉ ra hai cặp tam giác có độ dài ba cặp cạnh bằng nhau.

Lời giải:

Xét hai tam giác ABD và CDB có:

AB = CD (cùng có độ dài bằng 6 ô vuông).

AD = BC (cùng có độ dài bằng 4 ô vuông).

BD chung.

Do đó $△ ABD = △ CDB (c - c - c)$

Xét hai tam giác ACD và CAB có:

AD = BC (cùng có độ dài bằng 4 ô vuông).

CD = AB (cùng có độ dài bằng 6 ô vuông).

AC chung.

Do đó $△ ACD = △ CAB (c - c - c)$

Vậy hai cặp tam giác bằng nhau là: $△ ABD = △ CDB, △ ACD = △ CAB$

Bài 4.6 trang 67 Toán lớp 7: Cho Hình 4.20, biết $A B = C B, A D = C D, \hat{D A B} = 90^{\circ}, \hat{B D C} = 30^{\circ}$

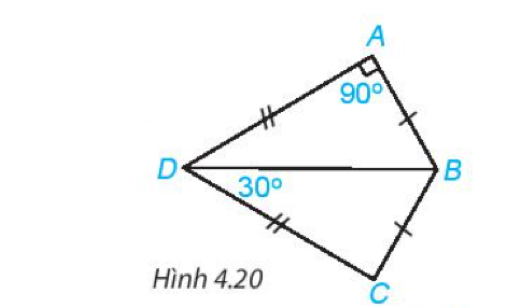
Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác | Kết nối tri thức (ảnh 1)

a) Chứng minh rằng $Δ A B D = Δ C B D$ .

b) Tính $\hat{A B C}$ .

Phương pháp giải:

a)Chứng minh ba cặp cạnh của hai tam giác bằng nhau.

b) $\hat{A B C} = \hat{A B D} + \hat{C B D}$

Lời giải:

a) Xét $Δ A B D$ và $Δ C B D$ có:

DA=DC(gt)

BD chung

BA=BC

Vậy $Δ A B D = Δ C B D$ (c.c.c)

b) Ta có $\hat{A} = \hat{C} = 90^{o}$ (hai góc tương ứng)

$\begin{array}{l} \hat{C} + \hat{C D B} + \hat{D B C} = 180^{o} \\ \Rightarrow 90^{o} + 30^{o} + \hat{D B C} = 180^{o} \\ \Rightarrow \hat{D B C} = 60^{o} \end{array}$