Bài 4 trang 80 Toán 10 Tập 2 | Cánh diều Giải toán lớp 10

Bài 4 trang 80 Toán 10 Tập 2 | Cánh diều Giải toán lớp 10

Van Anh Ngày: 15-03-2023 Lớp 10

5.9 K

Với giải Bài 4 trang 80 SGK Toán lớp 10 Cánh diều chi tiết trong Bài 3: Phương trình đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 3: Phương trình đường thẳng

Bài 4 trang 80 Toán lớp 10 Tập 2: Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0.

a) Lập phương trình tham số của đường thẳng d.

b) Tìm tọa độ điểm M thuộc d sao cho OM = 5 với O là gốc tọa độ.

c) Tìm tọa độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.

Lời giải:

a) Đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0.

Do đó d có 1 vectơ pháp tuyến là $\vec{n} = (1; - 2)$ , suy ra d có 1 vectơ chỉ phương là $\vec{u} = (2; 1)$

Cho y = 0, thay vào phương trình tổng quát của d ta được: x – 2 . 0 – 5 = 0 ⇔ x = 5.

Do đó, điểm A(5; 0) thuộc d.

Vậy phương trình tham số của đường thẳng d là

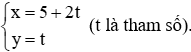
Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0

Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0

Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0

.

a) Lập phương trình tham số của đường thẳng d.

b) Tìm tọa độ điểm M thuộc d sao cho OM = 5 với O là gốc tọa độ.

c) Tìm tọa độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.

Lời giải:

a) Đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0.

Do đó d có 1 vectơ pháp tuyến là $\vec{n} = (1; - 2)$ , suy ra d có 1 vectơ chỉ phương là $\vec{u} = (2; 1)$

Cho y = 0, thay vào phương trình tổng quát của d ta được: x – 2 . 0 – 5 = 0 ⇔ x = 5.

Do đó, điểm A(5; 0) thuộc d.

Vậy phương trình tham số của đường thẳng d là

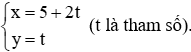
Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0

Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0

Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0

Xem thêm lời giải bài tập SGK Toán 10 Cánh diều hay, chi tiết khác:

Câu hỏi khởi động trang 73 Toán lớp 10 Tập 2: Một máy bay cất cánh từ sân bay theo một đường thẳng nghiêng với phương nằm ngang một góc 20°, vận tốc cất cánh là 200 km/h. Hình 24 minh họa hình ảnh đường bay của máy bay trên ra màn hình ra đa của bộ phận không lưu. Để xác định vị trí của máy bay tại những thời điểm quan trọng (chẳng hạn: 30 s, 60 s, 90 s, 120 s), người ta phải lập phương trình đường thẳng mô tả đường bay.....

Hoạt động 1 trang 73 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ $\vec{u} (\vec{u} \neq \vec{0})$ có giá song song (hoặc trùng) với đường thẳng ∆ (Hình 25).....

Hoạt động 2 trang 74 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có vectơ chỉ phương $\vec{u} = (a; b)$ . Xét điểm M(x; y) nằm trên ∆ (Hình 26).....

Luyện tập 1 trang 75 Toán lớp 10 Tập 2: Cho đường thẳng Δ có phương trình tham số....

Hoạt động 3 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ $\vec{n} (\vec{n} \neq \vec{0})$ có giá vuông góc với đường thẳng ∆ (Hình 27).....

Hoạt động 4 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có vectơ pháp tuyến $\vec{n} = (a; b)$ . Xét điểm M(x; y) nằm trên ∆ (Hình 28)....

Luyện tập 2 trang 76 Toán lớp 10 Tập 2: Cho đường thẳng Δ có phương trình tổng quát là x – y + 1 = 0.....

Hoạt động 5 trang 76 Toán lớp 10 Tập 2: Cho đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0). Nêu nhận xét về vị trí tương đối của đường thẳng ∆ với các trục tọa độ trong mỗi trường hợp sau:...

Bài 1 trang 79 Toán lớp 10 Tập 2: Lập phương trình tổng quát của đường thẳng Δ đi qua điểm A(– 1; 2) và...

Bài 2 trang 79 Toán lớp 10 Tập 2: Lập phương trình mỗi đường thẳng trong các Hình 34, 35, 36, 37 sau đây:....

Bài 3 trang 80 Toán lớp 10 Tập 2: Cho đường thẳng d có phương trình tham số là:....

Bài 4 trang 80 Toán lớp 10 Tập 2: Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0....

Bài 5 trang 80 Toán lớp 10 Tập 2: Cho tam giác ABC, biết A(1; 3); B(– 1; – 1); C(5; – 3). Lập phương trình tổng quát của....

Bài 6 trang 80 Toán lớp 10 Tập 2: Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng Δ ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng).....

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Giải SGK Toán 10 Bài 2: Biểu thức tọa độ của các phép toán

Giải SGK Toán 10 Bài 3: Phương trình đường thẳng

Giải SGK Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Giải SGK Toán 10 Bài 5: Phương trình đường tròn

Giải SGK Toán 10 Bài 6: Ba đường conic

Từ khóa :

toán 10 Giải bài tập phương trình đường thẳng

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

144

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

120

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

107

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

100

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.