Với giải Luyện tập 3 trang 9 Toán lớp 10 Kết nối tri thức với cuộc sống trong Bài 15: Hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 15: Hàm số
Luyện tập 3 trang 9 Toán 10 Tập 2: Vẽ đồ thị của các hàm số y = 3x + 1 và y = – 2x2. Hãy cho biết:
a) Hàm số y = 3x + 1 đồng biến hay nghịch biến trên ℝ.
b) Hàm số y = – 2x2 đồng biến hay nghịch biến trên mỗi khoảng: (– ∞; 0) và (0; + ∞).
Lời giải:
Vẽ các đồ thị hàm số:
* Hàm số y = 3x + 1
Tập xác định của hàm số là ℝ.
Với x = 0 thì y = 3 . 0 + 1 = 1
Với x = – 1 thì y = 3 . (– 1) + 1 = – 2
Vậy đồ thị hàm số y = 3x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; – 2).
* Hàm số y = – 2x2
Tập xác định của hàm số là ℝ.
Bảng giá trị tương ứng của x và y
|
x |
0 |
1 |
– 1 |
2 |
– 2 |
|
y = – 2x2 |
0 |
– 2 |
– 2 |
– 8 |
– 8 |
Trên mặt phẳng tọa độ, lấy năm điểm có tọa độ là (0; 0), (1; – 2), (– 1; – 2), (2; – 8), (– 2; – 8) rồi vẽ đường cong đi qua năm điểm trên ta được đồ thị của hàm số y = – 2x2.
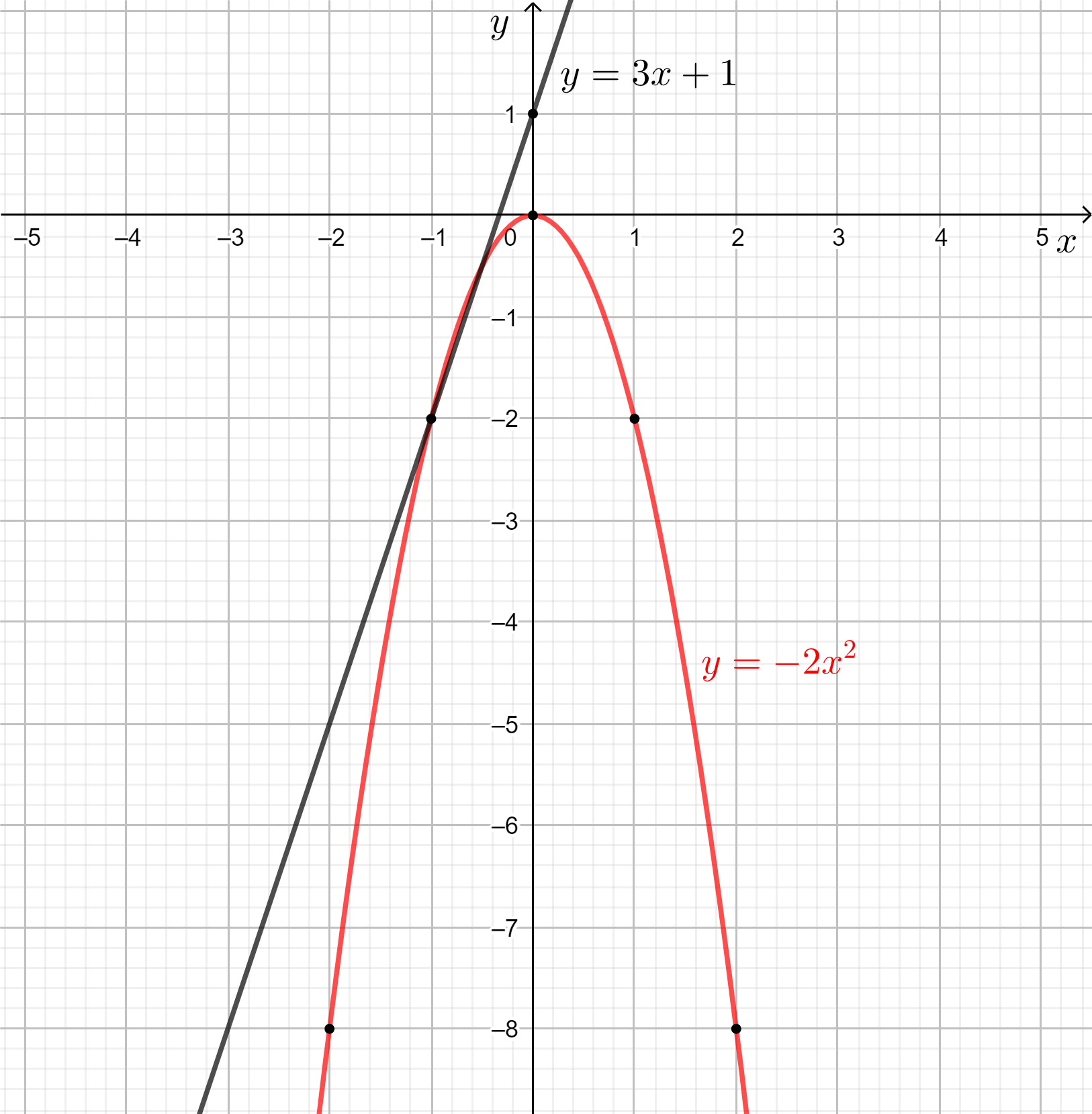
a) Từ hình trên trên, ta thấy đồ thị hàm số y = 3x + 1 đi lên từ trái sang phải trên ℝ nên hàm số y = 3x + 1 đồng biến trên ℝ.
b) Từ hình trên, ta có:
- Trên khoảng (– ∞; 0), đồ thị hàm số y = – 2x2 đi lên từ trái sang phải nên hàm số đồng biến trên khoảng này.
- Trên khoảng (0; + ∞), đồ thị hàm số y = – 2x2 đi xuống từ trái sang phải nên hàm số nghịch biến trên khoảng này.
Xem thêm các bài giải Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Hoạt động 2 trang 5 Toán 10 Tập 2: Quan sát Hình 6.1...
Hoạt động 3 trang 5 Toán 10 Tập 2: Tính tiền điện...
Luyện tập 2 trang 7 Toán 10 Tập 2:...
Hoạt động 6 trang 8 Toán 10 Tập 2: Quan sát đồ thị của hàm số y = f(x) = – x2 trên ℝ (H.6.5)...
Vận dụng 2 trang 9 Toán 10 Tập 2: Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7...
Bài 6.3 trang 9 Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:...
Bài 6.4 trang 9 Toán 10 Tập 2: Tìm tập xác định và tập giá trị của mỗi hàm số sau:...
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 17: Dấu của tam thức bậc hai
Bài 18: Phương trình quy về phương trình bậc hai
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack57. All Rights Reserved.
