Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 15: Hàm số chi tiết sách Toán 10 Tập 2 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 15: Hàm số

A. Các câu hỏi trong bài

Mở đầu trang 4 Toán 10 Tập 2: Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong tháng và số tiền phải trả (chưa tính thuế giá trị gia tăng). Có cách nào mô tả sự phụ thuộc của số tiền phải trả vào tổng lượng điện tiêu thụ hay không?

 

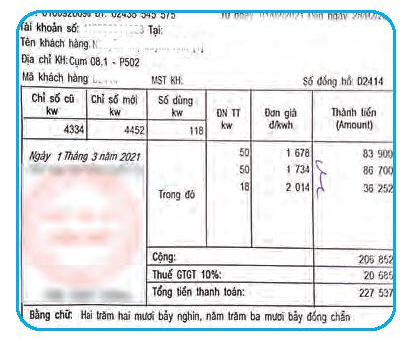
Lời giải:

Tổng lượng điện tiêu thụ trong tháng của khách hàng trên là: 50 + 50 + 18 = 118 (kWh).

Số tiền phải trả (chưa tính thuế giá trị gia tăng) là 206 852 đồng.

Giá tiền điện được tính theo bậc thang cho từng số lượng điện đã dùng.

Ở hóa đơn điện trên hình, người sử dụng điện dùng 118 kW, có nghĩa phải trả theo 3 bậc.

Nên ta tính số tiền điện bằng cách thực hiện phép tính:

50 . 1 678 + 50 . 1 734 + 18 . 2 014 = 206 852 (đồng).

Vậy số tiền điện phải trả phụ thuộc vào lượng điện tiêu thụ mỗi tháng.

Hoạt động 1 trang 5 Toán 10 Tập 2: Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:

Bảng 6.1 (Theo moitruongthudo.vn)

a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.

b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?

Lời giải:

a) Từ Bảng 6.1 ta có:

Nồng độ bụi PM 2.5 lúc 8 giờ là 57,9 μg/m3.

Nồng độ bụi PM 2.5 lúc 12 giờ là 60,07 μg/m3.

Nồng độ bụi PM 2.5 lúc 16 giờ là 81,78 μg/m3.

b) Mỗi thời điểm tương ứng với một giá trị của nồng độ bụi PM 2.5.

Hoạt động 2 trang 5 Toán 10 Tập 2: Quan sát Hình 6.1.

 

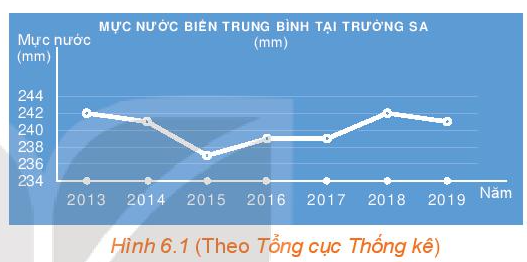
a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?

b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?

Lời giải:

a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong Hình 6.1 từ năm 2013 đến năm 2019.

b) Trong khoảng thời gian đó, mực nước biển trung bình tại Trường Sa thấp nhất vào năm 2015(khoảng 237 mm) và mực nước trung bình tại Trường Sa cao nhất vào năm 2013, năm 2018 (242 mm).

Hoạt động 3 trang 5 Toán 10 Tập 2: Tính tiền điện

Bảng 6.2

(Theo Tập đoàn Điện lực Việt Nam ngày 20-3-2019)

a) Dựa vào Bảng 6.2 về giá bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3:

Bảng 6.3

b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y vào x khi 0 ≤ x ≤ 50.

Lời giải:

a) Lượng điện tiêu thụ là 50 kWh thì ứng với mức tiêu thụ ở bậc 1 nên số tiền phải trả cho 50 kWh điện này là: 1 678 . 50 = 83 900 (đồng) = 83,9 (nghìn đồng).

Lượng điện tiêu thụ là 100 kWh thì 50 kWh đầu tính giá ở bậc 1 và 50 kWh sau tính giá ở bậc 2 nên số tiền phải trả cho 100 kWh điện này là:

1 678 . 50 + 1 734 . 50 = 170 600 (đồng) = 170,6 (nghìn đồng).

Lượng điện tiêu thụ là 200 kWh thì 50 kWh đầu tính giá ở bậc 1, 50 kWh tiếp theo tính giá ở bậc 2 và 100 kWh cuối tính  giá ở bậc 3 nên số tiền phải trả cho 200 kWh điện này là: 1 678 . 50 + 1 734 . 50 + 2 014 . 100 = 372 000 (đồng) = 372 (nghìn đồng).

Vậy ta điền vào bảng:

 

b) Gọi x là lượng điện tiêu thụ (đơn vị kWh), y là số tiền phải trả tương ứng (đơn vị nghìn đồng).

Do 0 ≤ x ≤ 50 nên lượng điện tiêu thụ thuộc mức điện bậc 1 với giá bán là 1 678 đồng/1 kWh hay chính là 1,678 nghìn đồng/1 kWh.

Khi đó, số tiền phải trả cho x (kWh) này là: y = 1,678 . x = 1,678x (nghìn đồng).

Vậy ta có công thức mô tả sự phụ thuộc của y vào x khi 0 ≤ x ≤ 50 là y = 1,678x.

Luyện tập 1 trang 6 Toán 10 Tập 2: a) Hãy cho biết Bảng 6.4 có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của hàm số đó.

Bảng 6.4 (Theo Tổng cục Thống kê)

b) Trở lại HĐ2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại x = 2018.

c) Cho hàm số y = f(x) = – 2x2. Tính f(1); f(2) và tìm tập xác định, tập giá trị của hàm số này.

Lời giải:

a) Từ Bảng 6.4 ta có: mỗi thời điểm xác định duy nhất một tuổi thọ trung bình của người Việt Nam nên bảng trên cho ta một hàm số.

Tập xác định của hàm số là: D = {2013; 2014; 2015; 2016; 2017; 2018}.

Tập giá trị của hàm số là: T = {73,1; 73,2; 73,3; 73,4; 73,5}.

b) Từ biểu đồ Hình 6.1 ta có ở năm 2018, mực nước biển trung bình tại Trường Sa là 242 mm.

Vậy giá trị của hàm số cho bằng biểu đồ trên tại x = 2018 là 242.

c) Ta có y = f(x) = – 2x2.

Do đó f(1) = – 2 . 12 = – 2; f(2) = – 2 . 22 = – 8.

Hàm số y = f(x) = – 2x2 xác định với mọi x ∈ ℝ.

Vậy tập xác định của hàm số trên là D = ℝ.

Vì x2 ≥ 0 với mọi x ∈ ℝ, suy ra 2x2 ≥ 0 với mọi x ∈ ℝ.

Nên y = – 2x2 ≤ 0 với mọi x ∈ ℝ.

Vậy tập giá trị của hàm số trên là T = (– ∞; 0].

Hoạt động 4 trang 7 Toán 10 Tập 2: Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số$y=\frac{1}{2}{x}^2$ .

(0; 0), (2; 2), (– 2; 2), (1; 2), (– 1; 2).

 

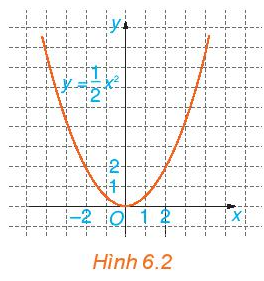
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.

Lời giải:

Xác định các điểm có tọa độ (0; 0), (2; 2), (– 2; 2), (1; 2), (– 1; 2) trên mặt phẳng tọa độ Oxy ở Hình 6.2, ta được

 

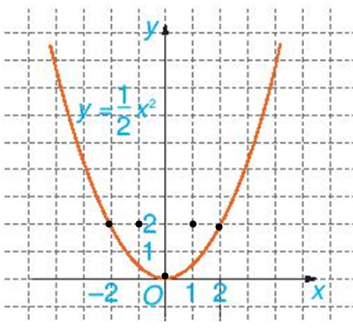
Quan sát hình trên ta thấy các điểm (0; 0), (2; 2), (– 2; 2) thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2$.

Với hoành độ x = 0, thay vào hàm số ta có y = $\frac{1}{2}$ . 02 = 0

Với x = 2, thay vào hàm số ta có y = $\frac{1}{2}$ . 22 = 2

Với x = – 2, thay vào hàm số ta có y = $\frac{1}{2}$ . (– 2)2 = 2.  

Vậy hoành độ và tung độ của những điểm nằm trên đồ thị thỏa mãn hàm số $y=\frac{1}{2}{x}^2$.

Luyện tập 2 trang 7 Toán 10 Tập 2:

a) Dựa vào đồ thị của hàm số $y=\frac{1}{2}{x}^2$ (H.6.2), tìm x sao cho y = 8.

b) Vẽ đồ thị của các hàm số y = 2x + 1 và y = 2x2 trên cùng một mặt phẳng tọa độ.

Lời giải:

a) Do y = 8 nên từ điểm tương ứng với số 8 trên trục Oy, ta kẻ đường thẳng song song với trục Ox, đường thẳng này cắt đồ thị hàm số $y=\frac{1}{2}{x}^2$ tại hai điểm. Từ hai điểm này, ta hạ đường thẳng vuông góc xuống trục Ox, ta thấy hai hình chiếu của hai điểm trên Ox là điểm 4 và – 4.

 

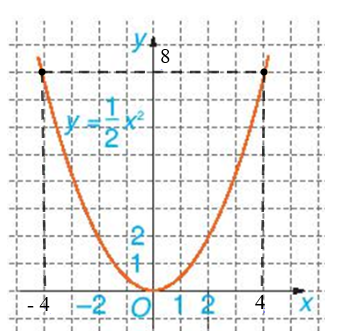
Vậy với y = 8 thì x = 4 hoặc x = – 4.

b) * Ta có: y = 2x + 1

Tập xác định của hàm số là ℝ.

Với x = 0 thì y = 2 . 0 + 1 = 1.

Với x = 1 thì y = 2 . 1 + 1 = 3.

Do đó đồ thị hàm số y = 2x + 1 là đường thẳng đi qua 2 điểm (0; 1) và (1; 3).

Ta vẽ đường thẳng đi qua 2 điểm (0; 1) và (1; 3).

* Ta có: y = 2x2

Tập xác định của hàm số là ℝ.

Ta có bảng giá trị tương ứng của x và y như sau:

 

Trên mặt phẳng tọa độ, vẽ đường cong đi qua các điểm (0; 0), (1; 2), (– 1; 2), (2; 8), (– 2; 8), đường cong này là đồ thị của hàm số y = 2x2.

 

Vận dụng 1 trang 7 Toán 10 Tập 2: Nếu lượng điện tiêu thụ từ 50 đến 100 kWh (50 < x ≤ 100) thì công thức liên hệ giữa y và x đã thiết lập ở HĐ3 không còn đúng nữa.

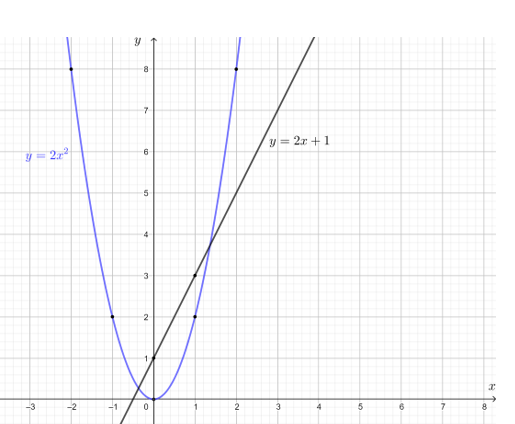
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:

y = 1,678 . 50 + 1,734(x – 50) = 83,9 + 1,734(x – 50) hay y = 1,734x – 2,8 (nghìn đồng).

Vậy trên tập xác định D = (50; 100], hàm số y mô tả số tiền phải thanh toán có công thức là y = 1,734x – 2,8; tập giá trị của nó là (83,9; 170,6].

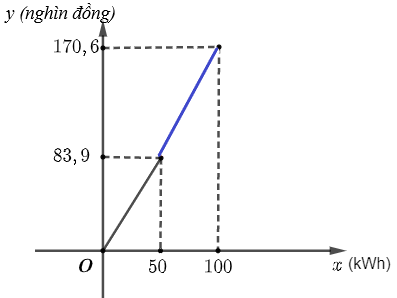
Hãy vẽ đồ thị ở Hình 6.3 vào vở rồi vẽ tiếp đồ thị của hàm số y = 1,734x – 2,8 trên tập D = (50; 100].

Lời giải:

Vẽ đồ thị hàm số y = 1,734x – 2,8 trên tập D = (50; 100].

Với x = 100 thì y = 170,6, đồ thị của hàm số là đoạn thẳng màu xanh trên hình sau:

 

Hoạt động 5 trang 8 Toán 10 Tập 2: Cho các hàm số y = – x + 1 và y = x. Tính giá trị y theo giá trị x để hoàn thành bảng sau:

x	– 2	– 1	0	1	2
y = – x + 1	?	?	?	?	?
y = x	?	?	?	?	?

 

Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số y = = – x + 1 và y = x tăng hay giảm?

Lời giải:

Ta thay các giá trị của x vào các hàm số đã cho để tính giá trị của y.

Ta tính được:

x	– 2	– 1	0	1	2
y = – x + 1	3	2	1	0	– 1
y = x	– 2	– 1	0	1	2

 

Từ bảng trên, ta nhận thấy, khi giá trị x tăng thì:

- Giá trị y tương ứng của hàm số y = – x + 1 giảm.

- Giá trị y tương ứng của hàm số y = x tăng.

Hoạt động 6 trang 8 Toán 10 Tập 2: Quan sát đồ thị của hàm số y = f(x) = – x2 trên ℝ (H.6.5).

 

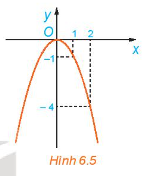
Hỏi:

a) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng (– ∞; 0)?

b) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng (0; + ∞)?

Lời giải:

a) Từ đồ thị Hình 6.5, ta thấy khi x tăng trên khoảng (– ∞; 0) thì đồ thị của hàm số đã cho đi lên từ trái sang phải, tức là giá trị của f(x) tăng trên khoảng này.

b) Từ đồ thị Hình 6.5, ta thấy khi x tăng trên khoảng (0; + ∞) thì đồ thị của hàm số đã cho đi xuống từ trái sang phải, tức là giá trị của f(x) giảm trên khoảng này.

Luyện tập 3 trang 9 Toán 10 Tập 2: Vẽ đồ thị của các hàm số y = 3x + 1 và y = – 2x2. Hãy cho biết:

a) Hàm số y = 3x + 1 đồng biến hay nghịch biến trên ℝ.

b) Hàm số y = – 2x2 đồng biến hay nghịch biến trên mỗi khoảng: (– ∞; 0) và (0; + ∞).

Lời giải:

Vẽ các đồ thị hàm số:

* Hàm số y = 3x + 1

Tập xác định của hàm số là ℝ.

Với x = 0 thì y = 3 . 0 + 1 = 1

Với x = – 1 thì y = 3 . (– 1) + 1 = – 2

Vậy đồ thị hàm số y = 3x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; – 2).

* Hàm số y = – 2x2

Tập xác định của hàm số là ℝ.

Bảng giá trị tương ứng của x và y

 

Trên mặt phẳng tọa độ, lấy năm điểm có tọa độ là (0; 0), (1; – 2), (– 1; – 2), (2; – 8), (– 2; – 8) rồi vẽ đường cong đi qua năm điểm trên ta được đồ thị của hàm số y = – 2x2.

 

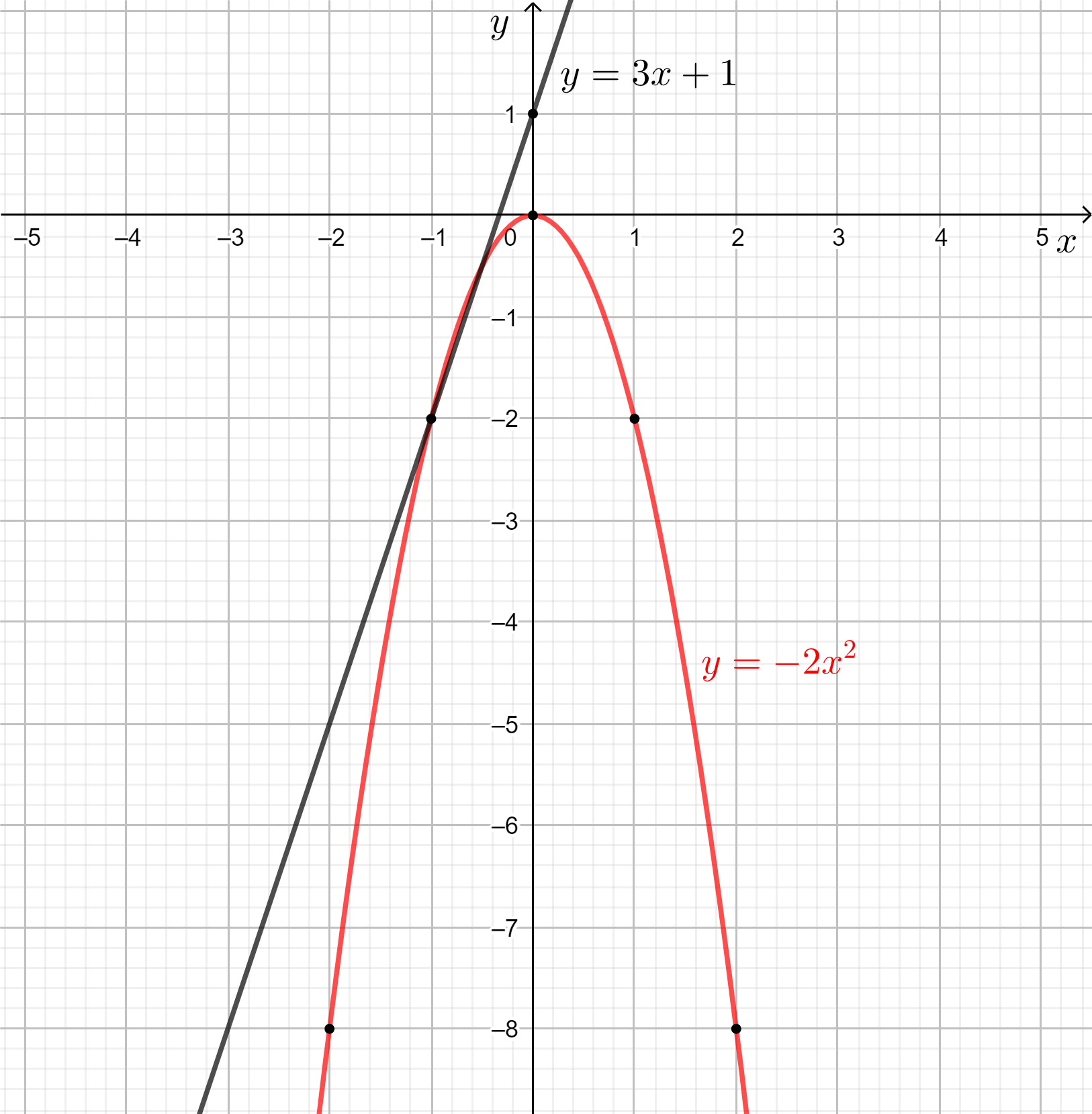
a) Từ hình trên trên, ta thấy đồ thị hàm số y = 3x + 1 đi lên từ trái sang phải trên ℝ nên hàm số y = 3x + 1 đồng biến trên ℝ.

b) Từ hình trên, ta có:

- Trên khoảng (– ∞; 0), đồ thị hàm số y = – 2x2 đi lên từ trái sang phải nên hàm số đồng biến trên khoảng này.

- Trên khoảng (0; + ∞), đồ thị hàm số y = – 2x2 đi xuống từ trái sang phải nên hàm số nghịch biến trên khoảng này.

Vận dụng 2 trang 9 Toán 10 Tập 2: Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.

 

a) Tính số tiền phải trả khi di chuyển 25 km.

b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.

c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.

Lời giải:

a) Khi di chuyển 25 km thì khách hàng phải trả 10 000 đồng cho 0,6 km đầu tiên (giá mở cửa) và 13 000 đồng cho mỗi km của  24,4 km (25 – 0,6) sau (đây là giá tính cho km tiếp theo dưới 25 km).

Tổng số tiền phải trả khi di chuyển 25 km là: 10 000 + 24,4 . 13 000 = 327 200 (đồng).

Vậy số tiền phải trả khi di chuyển 25 km là 327 200 đồng.

b) Gọi x (km, x > 0) là độ dài quãng đường di chuyển và y (đồng) là số tiền phải trả tương ứng.

Từ bảng giá cước, ta có:

- Giá mở cửa là 10 000 đồng cho 0,6 km đầu tiên, có nghĩa là khi x ≤ 0,6 thì số tiền phải trả tương ứng là y = 10 000.

- Giá tiền cho km tiếp theo đến dưới 25 km là 13 000 đồng cho mỗi km, có nghĩa là khi 0,6 < x ≤ 25 thì số tiền phải tương ứng là y = 10 000 + 13 000(x – 0,6) hay y = 13 000x + 2 200.

- Giá tiền phải trả cho km thứ 25 trở lên là 11 000 đồng cho mỗi km, có nghĩa là khi x > 25 thì số tiền phải trả tương ứng là y = 10 000 + 13 000 . 24,4 + 11 000(x – 25) hay y = 11 000 x + 52 200.

Vậy ta có công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển là:

$y=\left\{\begin{array}{l}10\mathrm{000,}x\le \mathrm{0,6}\\ 13000x+2\mathrm{200,}\mathrm{0,6}<x\le 25\\ 11000x+52\mathrm{200,}x>25.\end{array}\right.$

c) Ta vẽ đồ thị hàm số $y=\left\{\begin{array}{l}10\mathrm{000,}x\le \mathrm{0,6}\\ 13000x+2\mathrm{200,}\mathrm{0,6}<x\le 25\\ 11000x+52\mathrm{200,}x>25\end{array}\right.$.

Để vẽ đồ thị hàm số trên, ta vẽ các đồ thị y = 10 000 trên (0; 0,6], đồ thị y = 13 000x + 2 200 trên (0,6; 25] và đồ thị y = 11 000x + 52 200 trên (25; + ∞), mỗi đồ thị cần vẽ là một đoạn thẳng trên khoảng tương ứng.

Vậy ta vẽ được đồ thị hàm số trên:

 

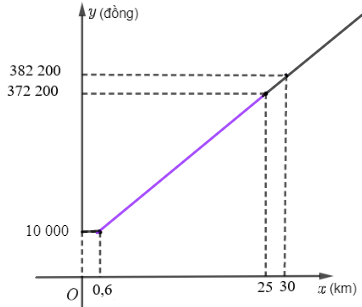
Từ hình trên, ta thấy đồ thị hàm số $y=\left\{\begin{array}{l}10\mathrm{000,}x\le \mathrm{0,6}\\ 13000x+2\mathrm{200,}\mathrm{0,6}<x\le 25\\ 11000x+52\mathrm{200,}x>25\end{array}\right.$ đi lên từ trái sang phải trên (0,6; + ∞).

Vậy hàm số này đồng biến trên (0,6; + ∞).

B. Bài tập

Bài 6.1 trang 9 Toán 10 Tập 2: Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x?

a) x + y = 1;

b) y = x2;

c) y2 = x;

d) x2 – y2 = 0.

Lời giải:

a) Ta có: x + y = 1 ⇒ y = – x + 1.

Với mỗi giá trị thực của x, ta đều xác định được duy nhất một giá trị thực của y.

Vậy y là hàm số của x.

b) y = x2

Với mỗi giá trị thực của x, ta đều xác định được duy nhất một giá trị thực của y.

Vậy y là hàm số của x.

c) y2 = x

Với x = 1 thì y2 = 1, khi đó y = 1 hoặc y = – 1 nên với một giá trị của x, ta xác định được hai giá trị của y tương ứng, vậy y không phải là hàm số của x.

d) x2 – y2 = 0 ⇔ y2 = x2.

Với x = 1 ⇒ x2 = 12 = 1, do đó y2 = 1 nên y = 1 hoặc y = – 1, do đó với một giá trị của x, ta xác định được hai giá trị của y tương ứng, vậy y không phải là hàm số của x.

Bài 6.2 trang 9 Toán 10 Tập 2: Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.

Lời giải:

Có nhiều ví dụ, chẳng hạn ta có bảng 8 số nguyên tố đầu tiên:

 

Tập xác định là D = {1; 2; 3; 4; 5; 6; 7; 8}.

Tập giá trị là {2; 3; 5; 7; 11; 13; 17; 19}.

Bài 6.3 trang 9 Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:

a) y = 2x3 + 3x + 1;

b) $y=\frac{x-1}{x^2-3x+2}$;

c) $y=\sqrt{x+1}+\sqrt{1-x}$.

Lời giải:

a) Biểu thức 2x3 + 3x + 1 có nghĩa với mọi số thực x.

Vậy tập xác định của hàm số là D = ℝ.

b) Biểu thức $\frac{x-1}{x^2-3x+2}$có nghĩa khi x2 – 3x + 2 ≠ 0

⇔ x2 – x – 2x + 2 ≠ 0

⇔ x(x – 1) – 2(x – 1) ≠ 0

⇔ (x – 1)(x – 2) ≠ 0

⇔ x – 1 ≠ 0 và x – 2 ≠ 0

⇔ x ≠ 1 và x ≠ 2.

Vậy tập xác định của hàm số là D = ℝ\{1; 2}.

c) Biểu thức $\sqrt{x+1}+\sqrt{1-x}$ có nghĩa khi $\left\{\begin{array}{l}x+1\ge 0\\ 1-x\ge 0\end{array}\right.$$\iff \left\{\begin{array}{l}x\ge -1\\ x\le 1\end{array}\right.\iff -1\le x\le 1$

Vậy tập xác định của hàm số là D = [– 1; 1].

Bài 6.4 trang 9 Toán 10 Tập 2: Tìm tập xác định và tập giá trị của mỗi hàm số sau:

a) y = 2x + 3;

b) y = 2x2.

Lời giải:

a) y = 2x + 3

Biểu thức 2x + 3 có nghĩa với mọi số thực x.

Vậy tập xác định của hàm số là D = $ℝ$.

Với mỗi giá trị bất kì của x, ta đều tìm được một giá trị của y tương ứng.

Vậy tập giá trị của hàm số là ℝ.

b) y = 2x2

Biểu thức 2x2 có nghĩa với mọi số thực x.

Vậy tập xác định của hàm số này là D = ℝ.

Ta có: x2 ≥ 0 với mọi x ∈ ℝ.

Do đó 2x2 ≥ 0 với mọi x ∈ ℝ.

Vậy tập giá trị của hàm số trên là [0; + ∞).   

Bài 6.5 trang 9 Toán 10 Tập 2: Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.

a) y = – 2x + 1;

b) $y=-\frac{1}{2}{x}^2$.

Lời giải:

a) y = – 2x + 1

Tập xác định của hàm số này là D = ℝ.

Với x = 0 thì y = 1, với x = 1 thì y = – 1.

Đồ thị hàm số y = – 2x + 1 là đường thẳng đi qua 2 điểm (0; 1) và (1; – 1).

 

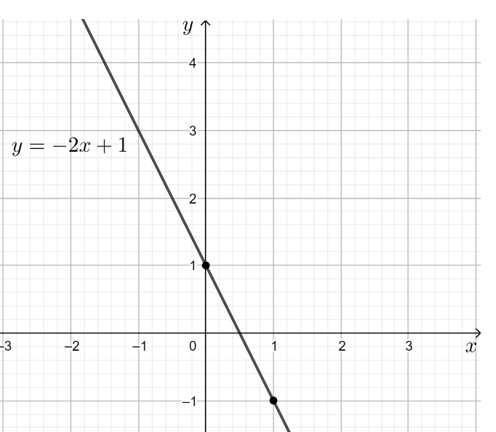
Đồ thị hàm số đi xuống từ trái qua phải trên ℝ nên hàm số nghịch biến trên ℝ.

b) $y=-\frac{1}{2}{x}^2$

Tập xác định của hàm số này là D = ℝ.

Bảng giá trị của x và y tương ứng:

x	0	1	– 1	2	– 2
y	0	$-\frac{1}{2}$	$-\frac{1}{2}$	– 2	– 2

Đồ thị hàm số $y=-\frac{1}{2}{x}^2$ là đường cong đi qua 5 điểm (0; 0), $\left(1;-\frac{1}{2}\right),\left(-1;-\frac{1}{2}\right)$, (2; – 2), (– 2; – 2).

 

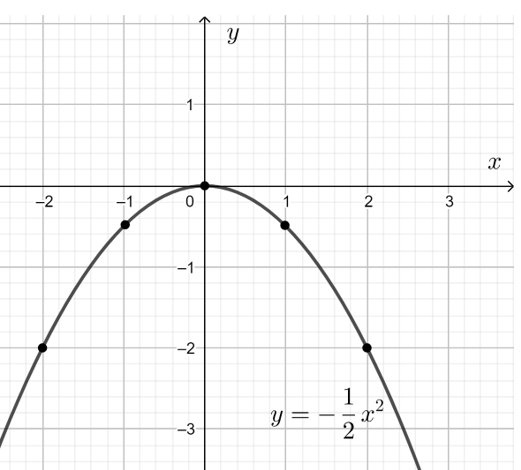
Ta thấy đồ thị hàm số đi lên từ trái sang phải trên (– ∞; 0) và đi xuống từ trái sang phải trên (0; + ∞).

Vậy hàm số đồng biến trên khoảng (– ∞; 0) và nghịch biến trên khoảng (0; + ∞).

Bài 6.6 trang 9 Toán 10 Tập 2: Giá thuê xe ô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe.

a) Viết công thức của hàm số T = T(x).

b) Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này.

Lời giải:

a) Đổi: 1,2 triệu đồng = 1 200 000 đồng; 900 nghìn đồng = 900 000 đồng.

Gọi số ngày khách thuê xe là x (ngày), số tiền khách phải trả tương ứng là T (đồng).

Giá xe cho mỗi ngày trong 2 ngày đầu tiên là 1 200 000 đồng nên khi x ≤ 2 thì số tiền phải trả là: T = 1 200 000x.

Giá tiền khách phải trả khi thuê 2 ngày đầu là: 1 200 000 . 2 = 2 400 000 (đồng).

Khách thuê tiếp sau 2 ngày đầu, giá xe cho mỗi ngày trong các ngày tiếp theo là 900 000 đồng, hay với x > 2 thì số tiền phải trả là: T = 2 400 000 + 900 000(x – 2).

Vậy ta có hàm số $T=\left\{\begin{array}{l}1200000xn{ê}^{\text{'}}ux\le 2\\ 2400000+900000\left(x-2\right)n{ê}^{\text{'}}ux>2.\end{array}\right.$

b)

T(2) = 1 200 000 . 2 = 2 400 000, khách sẽ phải trả 2 400 000 đồng nếu thuê xe 2 ngày;

T(3) = 2 400 000 + 900 000.(3 – 2) = 3 300 000, khách sẽ phải trả 3 300 000 đồng nếu thuê xe 3 ngày;

T(5) = 2 400 000 + 900 000.(5 – 2) = 5 100 000, khách sẽ phải trả 5 100 000 đồng nếu thuê xe 5 ngày.

Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 5

Bài 16 : Hàm số bậc hai

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai

Lý thuyết Hàm số

1. Khái niệm hàm số

Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực ℝ thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D gọi là tập xác định của hàm số.

Tập tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số.

Ví dụ : Viết hàm số mô tả sự phụ thuộc giữa diện tích S và bán kính r của hình tròn. Tìm tập xác định của hàm số đó.

Hướng dẫn giải

Diện tích S của hình tròn phụ thuộc vào bán kính r theo công thức S = π.r², trong đó r là biến số, S = S(r) là hàm số của r.

Vì r là bán kính của hình tròn nên r > 0.

Do đó tập xác định của hàm số S = π.r² là D = (0 ; +∞).

Vậy hàm số mô tả sự phụ thuộc giữa diện tích và bán kính của hình tròn là: S = S(r) = π.r² và tập xác định của hàm số đó là: D = (0 ; +∞).

Chú ý : Khi cho hàm số bằng công thức y = f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

Ví dụ :

a) Tìm tập xác định của hàm y = $\sqrt{x+3}$

b) Tìm tập xác định của hàm y = $\frac{2x+4}{-x-1}$

Hướng dẫn giải

a) Biểu thức $\sqrt{x+3}$ có nghĩa khi x + 3 ≥ 0, tức là x ≥ – 3.

Vậy tập xác định của hàm số y = $\sqrt{x+3}$ là D = [– 3 ; +∞).

b) Biểu thức $\frac{2x+4}{-x-1}$ có nghĩa khi –x – 1 ≠ 0, tức là x ≠ –1.

Vậy tập xác định của hàm số y = $\frac{2x+4}{-x-1}$ là D = ℝ\{–1}.

Nhận xét : Một hàm số có thể cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời.

Ví dụ :

a) Hàm số cho bởi công thức như hàm số y = f(x) = 2x + 7 ;

b) Nhiệt độ T(^°C) tại các thời điểm t (giờ) trong cùng một ngày được cho bởi bảng sau :

Nhiệt độ T(^°C) phụ thuộc vào sự thay đổi của thời gian t (giờ) và mỗi giờ chỉ tương ứng với đúng một giá trị nhiệt độ nên tương ứng đó xác định một hàm số.

Vậy bảng trên biểu thị một hàm số.

c) Cho biểu đồ sau:

Quan sát biểu đồ trên ta thấy ứng với mỗi ngày chỉ có đúng một giá trị lượng mưa nên tương ứng đó xác định một hàm số.

Vậy biểu đồ trên biểu thị một hàm số.

2. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x ; f(x)) trên mặt phẳng tọa độ với mọi x thuộc D.

Ví dụ: Tìm tập xác định và vẽ đồ thị của hàm số y = 2x trên mặt phẳng tọa độ.

Hướng dẫn giải

Vì 2x xác định với mọi x ∈ℝ nên tập xác định của hàm số y = 2x là D = ℝ.

Đồ thị của hàm số y = 2x là một đường thẳng đi qua gốc tọa độ như trong hình sau :

3. Sự đồng biến, nghịch biến của hàm số

- Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a ; b), nếu

∀ x₁, x₂ ∈ (a ; b), x₁ < x₂ ⇒ f(x₁) < f(x₂).

- Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a ; b), nếu

∀ x₁, x₂ ∈ (a ; b), x₁ < x₂ ⇒ f(x₁) > f(x₂).

Chú ý:

- Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải;

- Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.

Ví dụ: Cho hàm số y = –x² có đồ thị hàm số như hình sau:

Hàm số y = –x² đồng biến hay nghịch biến trên mỗi khoảng (–∞; 0) và (0; +∞).

Hướng dẫn giải

Quan sát đồ thị hàm số y = –x² ta thấy trên khoảng (–∞; 0), đồ thị đi lên từ trái sang phải. Do đó hàm số đồng biến trên khoảng (–∞; 0).

Ta thấy trên khoảng (0; +∞), đồ thị đi xuống từ trái sang phải. Do đó hàm số nghịch biến trên khoảng (0; +∞).

Vậy hàm số y = –x² đồng biến trên khoảng (–∞; 0) và nghịch biến trên khoảng (0; +∞).