Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 10 Chương 4: Hệ thức lượng trong tam giác. Vectơ sách Cánh diều. Bài viết gồm 30 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 10.
Trắc nghiệm Toán 10 Chương 4: Hệ thức lượng trong tam giác. Vectơ
Câu 1. Cho hình vuông ABCD. Khẳng định nào sau đây đúng?
A.
B.
C.
D. Hai vectơ cùng hướng.
Đáp án đúng là: C
Vì
Câu 2. Tam giác ABC có . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.
A. ;
B. ;
C. ;
D. ;
Đáp án đúng là: C
Áp dụng định lý hàm số cosin, ta có:
(đơn vị độ dài).
Ta có: (đơn vị diện tích).
Lại có (đơn vị độ dài).
Câu 3. Cho và là các vectơ khác với là vectơ đối của . Khẳng định nào sau đây sai?
A. Hai vectơ cùng phương;
B. Hai vectơ ngược hướng;
C. Hai vectơ cùng độ dài;
D. Hai vectơ chung điểm đầu.
Đáp án đúng là: D
Ta có : . Do đó, và cùng phương, cùng độ dài và ngược hướng nhau.
Câu 4. Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để ?
A. ABCD là hình bình hành.
B. ABCD là hình tứ giác
C. AC = BD
D. AB = CD
Đáp án đúng là : A
Ta có:
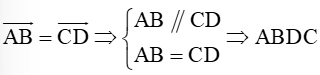
Mặt khác, ABCD là hình bình hành 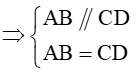
Do đó, điều kiện cần và đủ để là ABCD là hình bình hành.
Câu 5. Cho hình thoi ABCD cạnh bằng 1cm và có . Tính độ dài AC.
A.
B.
C.
D. AC = 2.
Đáp án đúng là: A
Do ABCD là hình thoi, có .
Theo định lí hàm cosin, ta có:
Câu 6. Tam giác ABC có . Số đo góc bằng:
A.
B.
C.
D.
Đáp án đúng là: C
Theo định lí hàm cosin, ta có:.
Do đó, .
Câu 7. Tam giác ABC có . Tính diện tích tam giác ABC.
A. ;
B.;
C. ;
D. .
Đáp án đúng là: C
Ta có: .
Suy ra tam giác ABC cân tại A nên .
Diện tích tam giác ABC là (đơn vị diện tích)
Câu 8. Cho tam giác ABC, có bao nhiêu vectơ khác vectơ - không, có điểm đầu và điểm cuối là các đỉnh A, B, C.
A. 3
B. 6
C. 4
D. 9
Đáp án đúng là: B
Đó là các vectơ:
Câu 9. Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ - không, cùng phương với có điểm đầu và điểm cuối là các đỉnh của lục giác là
A. 4;
B. 6;
C. 7;
D. 9.
Đáp án đúng là: B
Đó là các vectơ: .
Câu 10. Tam giác ABC có và . Tính độ dài cạnh BC.
A.
B.
C.
D.
Đáp án đúng là: B
Theo định lí hàm cosin, ta có:
- .BC + 1 = 0
.
Câu 11. Cho tam giác OAB vuông cân tại O cạnh OA = a. Khẳng định nào sau đây sai:
Đáp án đúng là: C
Dựa vào các đáp án, ta có nhận xét sau:
- Gọi C nằm trên tia đối của tia AO sao cho
Và D nằm trên tia đối của tia BO sao cho
Dựng hình chữ nhật OCED suy ra (quy tắc hình bình hành).
Ta có:
Do đó, A đúng
- B đúng, vì
- D đúng, vì
Vậy chỉ còn đáp án C.
Câu 12. Cho tam giác ABC cân ở A, đường cao AH. Khẳng định nào sau đây sai?
A.
B.
C.
D.
Đáp án đúng là : A
Tam giác ABC cân ở A, đường cao AH. Do đó, H là trung điểm BC (tính chất tam giác cân).
Ta có:
- 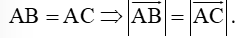
- H là trung điểm 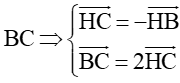
Câu 13. Cho tứ giác ABCD. Trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho và Tính vectơ theo hai vectơ
A.
B.
C.
D.
Đáp án đúng là: C
Ta có : và
Suy ra
Theo bài ra, ta có: và Thật vậy:
Vậy
Câu 14. Cho hình chữ nhật ABCD, hai đường đường chéo AC và BD cắt nhau tại O. Tính hiệu - :
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: D
Áp dụng quy tắc 3 điểm cho A, B, D ta có: - = .
Câu 15. Tam giác ABC có . Gọi D là chân đường phân giác trong góc . Khi đó góc bằng bao nhiêu độ?
A.
B.
C.
D.
Đáp án đúng là: C
Theo định lí hàm cosin, ta có:
Trong có .
Câu 16. Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng ?
A.
B.
C.
D.
Đáp án đúng là: C
Xét các đáp án ta thấy cần phân tích vectơ theo hai vectơ và
Vì ABCD là hình bình hành nên
Và M là trung điểm AB nên
suy ra
Câu 17. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây sai?
A.
B.
C.
D.
Đáp án đúng là: D
Ta có: 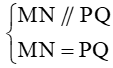
Do đó MNPQ là hình bình hành.
Vì MNPQ là hình bình hành nên
Câu 18. Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:
A. ;
B.
C. ;
D. .
Đáp án đúng là: C
Vì F là trung điểm của AC
Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.
Khi đó:
Vậy diện tích tam giác GFC là:
Câu 19. Cho tam giácABC đều cạnh a.Tính
Đáp án đúng là: A
Gọi H là trung điểm của
Xét tam giác vuông AHC ta có:
Suy ra
Ta lại có
Suy ra :
Câu 20. Cho tam giác ABC có M là trung điểm của BC. Tính theo và
A.
B.
C.
D.
Đáp án đúng là: C
Ta có :
Câu 21. Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
A.
B.
C.
D. 2.
Đáp án đúng là: D
Theo định lí hàm sin, ta có:
Do đó, độ dài OB lớn nhất khi và chỉ khi
.
Khi đó OB = 2.
Câu 22. Cho tam giác ABC, gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho . Gọi K là trung điểm của MN. Khi đó :
A.
B.
C.
D.
Đáp án đúng là: C
Vì K là trung điểm của MN nên ta có :
Ta có : .
Mà M là trung điểm của AB và N là điểm thuộc cạnh AC sao cho NC = 2AN nên ta có :
Do đó,
Câu 23. Cho hai vectơ và thỏa mãn 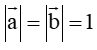
A.
B.
C.
D.
Đáp án đúng là: B
Ta có:
Suy ra
Câu 24. Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng
A.
B.
C.
D.
Đáp án đúng là: C
Xác định được góc là góc ngoài của góc nên (do tam giác ABC là tam giác đều nên góc , do đó, góc ngoài của góc B có số đo là 120o).
Do đó
Câu 25. Cho hình chữ nhật ABCD, hai đường đường chéo AC và BD cắt nhau tại O. Tính hiệu -
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: D
Ta có: 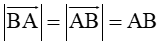
Câu 26. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
A. ;
B. ;
C.
D. .
Đáp án đúng là: C
Xét tam giác ABC đều, có độ dài cạnh bằng a.
Theo định lí sin, ta có: (đơn vị độ dài).
Vậy diện tích cần tính là:
Câu 27. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
A.
B.
C.
D.
Đáp án đúng là: C
- Xác định được góc là góc nên (do tam giác ABC đều)
Do đó A đúng
- Xác định được góc là góc ngoài của góc nên
Do đó B đúng.
- Xác định được góc là góc nên
Ta có: AG nằm trên đường trung tuyến cũng chính là đường cao của tam giác đều ABC, ta tính được đường cao, suy ra: AG = .a.= .
Tương tự, GB = .
Do đó C sai.
- Xác định được góc là góc nên
Do đó D đúng.
Câu 28. Cho tam giác ABC vuông tại A và có AB = c; AC = b. Tính
A.>
B.
C.
D.
Đáp án đúng là: B
Áp dung định lý Py – ta – go ta có:
Cos B =
Lại có: cos B chính là cos
Ta có:
Câu 29. Tam giác ABC có và độ dài đường cao AH = 2. Tính độ dài cạnh AB.
A. AB = 2;
B. ;
C. AB = 2 hoặc ;
D. AB = 2 hoặc .
Đáp án đúng là: C
Nửa chu vi là:
Ta có: .
Suy ra .
Lại có (đơn vị diện tích).
Từ đó ta có:
Câu 30.Cho tam giác ABC có Gọi M là trung điểm cạnh BC Tính
A.
B.
C.
D.
Đáp án đúng là: A
Vì M là trung điểm của BC suy ra
Khi đó
Xem thêm các bài trắc nghiệm Toán 10 Cánh diều hay, chi tiết khác:
Trắc nghiệm Toán 10 Bài 6: Tích vô hướng của hai vectơ
Trắc nghiệm Toán 10 Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây