Với giải Bài 4 trang 30 Toán lớp 10 Cánh diều chi tiết trong Bài tập cuối chương II giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài tập cuối chương II

Bài 4 trang 30 Toán lớp 10: Bác Ngọc thực hiện chế độ ăn kiêng với yêu cầu tối thiểu hằng ngày qua thức uống là 300 ca-lo, 36 đơn vị vitamin A và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca-lo, 12 đơn vị vitamin A và 10 đơn vị vitamin C. Một cốc đổ uống ăn kiêng thứ hai cung cấp 60 ca-lo, 6 đơn vị vitamin A và 30 đơn vị vitamin C.

a) Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ.

b) Chỉ ra hai phương án mà bác Ngọc có thể chọn lựa số lượng cốc cho đồ uống thứ nhất và thứ hai nhằm đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ.

Lời giải:

a) Gọi x, y lần lượt là số lượng cốc cho đồ uống thứ nhất và thứ hai cần tìm.

Lượng calo trong cả 2 đồ uống là: 60x+60y

Lượng vitamin A trong 2 đồ uống là: 12x+6y

Lượng vitamin C trong 2 đồ uống là: 10x+30y

Ta có hệ bất phương trình:

$\{\begin{array}{l}60x+60y\ge 300\\ 12x+6y\ge 36\\ 10x+30y\ge 90\end{array}$

b)

+) Thay cặp số (2;4) vào hệ ta được:

60.2+60.2=360>300

2.12+4.6=48>36

2.10+4.30=140>90

=> (2;4) là một nghiệm của hệ.

+) Thay cặp số (1;5) vào hệ ta được:

1.60+5.60=360>300

1.12+5.6=42>36

1.10+5.30=160>90

=> (1;5) là một nghiệm của hệ.

Vậy hai phương án bác Ngọc có thể chọn là:

Phương án 1: 2 cốc loại 1 và 4 cốc loại 2.

Phương án 2: 1 cốc loại 1 và 5 cốc loại 2.

Bài tập vận dụng:

Bài 1. Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) $\frac{x}{3}+\frac{y}{2}<-1$                          

b) $x-\frac{3y}{2}\le 0$                           

c) $\frac{x+y}{2}\ge \frac{2x-y+1}{3}$ 

Hướng dẫn giải:

a) Dựng đường thẳng $\frac{x}{3}+\frac{y}{2}=-1$.

Thay giá trị (0 ; 0) vào bất phương trình, ta có $\frac{0}{2}+\frac{0}{3}=0<-1$ là mệnh đề sai.

Miền nghiệm là miền không chứa điểm (0 ; 0), không tính đường thẳng biên.

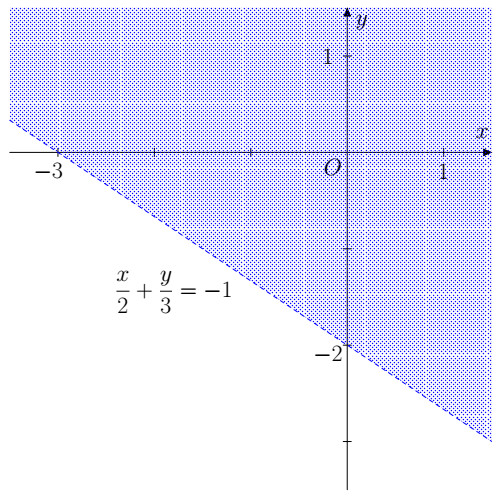
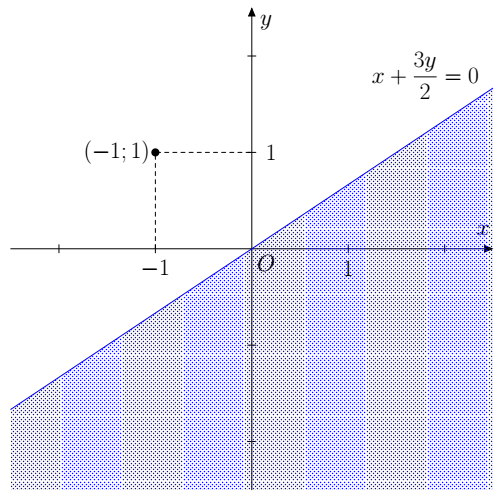
b) Dựng đường thẳng $x-\frac{3y}{2}=0$.

Lấy điểm (–1 ; 1) ta có: $-1-\frac{3.1}{2}=-\frac{5}{2}\le 0$ là mệnh đề đúng.

Miền nghiệm là miền chứa điểm (–1 ; 1) kể cả đường thẳng biên.

c) $\frac{x+y}{2}\ge \frac{2x-y+1}{3}$⇔3.(x + y) $\ge$ 2.(2x – y + 1) ⇔ x – 5y ≤ –2

Dựng đường thẳng x – 5y = –2.

Thay giá trị (0 ; 0) vào bất phương trình, ta có 0 – 0 = 0 ≤ –2 là mệnh đề sai.

Miền nghiệm là miền không chứa điểm (0 ; 0), kể cả đường thẳng biên.

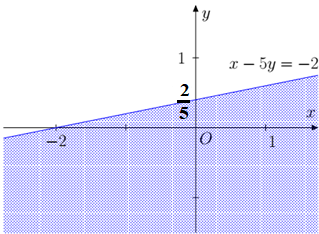
Bài 2. Một gian hàng trưng bày bàn và ghế rộng 60m². Diện tích để kê một chiếc ghế là 0,5m², một chiếc bàn là 1,2m². Gọi x là số ghế và y là số bàn được kê (x ≥ 0, y ≥ 0)

a) Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn ghế.

b) Chỉ ra ba nghiệm của bất phương trình trên.

Hướng dẫn giải:

a) Diện tích kê x chiếc ghế và y chiếc bàn là 0,5x + 1,2y (m²).

Diện tích này không thể lớn hơn 60m² nên ta được bất phương trình cần tìm:

0,5x + 1,2y ≤ 60 hay 5x + 12y ≤ 600.

b) Lấy ví dụ các cặp giá trị (10 ; 10), (30; 15), (24; 40), ta có:

5 . 10 + 12 . 10 = 170 ≤ 600 là mệnh đề đúng.

5 . 30 + 12 . 15 = 330 ≤ 600 là mệnh đề đúng.

5 . 24 + 12 . 40 = 600 ≤ 600 là mệnh đề đúng.

Vậy (10 ; 10), (30; 15), (24; 40) là ba nghiệm của bất phương trình 5x + 12y ≤ 600.

Bài 3. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chừa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn, giá thịt bò là 250 nghìn/kg và thịt lợn là 160 nghìn/kg. Tính xem gia đình cần mua bao nhiêu kg mỗi loại thịt để chi phí là ít nhất.

Hướng dẫn giải:

Giả sử mỗi ngày gia đình này mua x kg thịt bò và y kg thịt lợn.

Điều kiện 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,2.

Lượng protein và lipit trong thức ăn hàng ngày lần lượt là:

P = 800x + 600y ≥ 900 (đơn vị)

L = 200x + 400y ≥ 400 (đơn vị)

Từ đó, ta có hệ bất phương trình: $\left\{\begin{array}{l}0\le x\le 1,6\\ 0\le y\le 1,2\\ 8x+6y\ge 9\\ 2x+4y\ge 4\end{array}\right.$ 

Miền nghiệm của hệ bất phương trình được giới hạn bởi tứ giác ABCD, trong đó:

A(0,225 ; 1,2), B(1,6 ; 1,2), C(1,6 ; 0,2), D(0,6 ; 0,7).

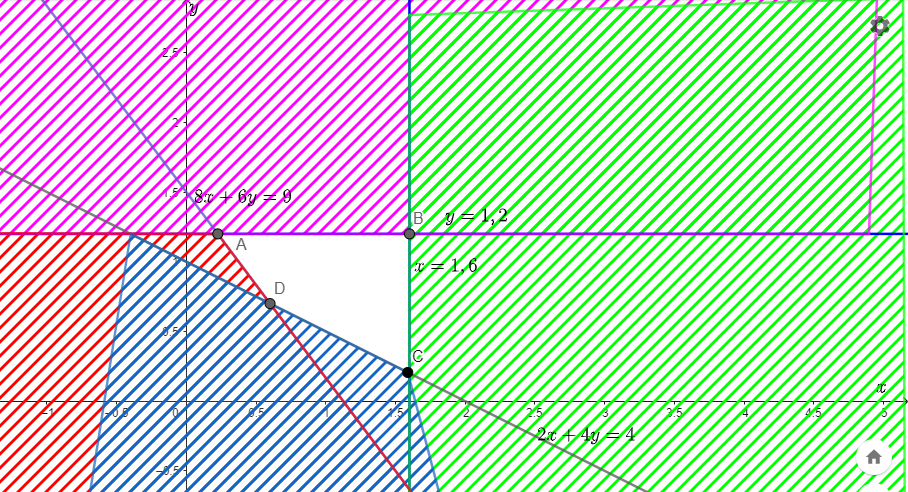
Số tiền mua thức ăn hàng ngày là:

T = 250x + 160y (nghìn đồng)

Xét giá trị của T tại các đỉnh của tứ giác ABCD, ta có:

Tại A(0,225 ; 1,2), với x = 0,225 và y = 1,2 thì T = 250.0,225 + 160.1,2 = 248,25;

Tại B(1,6 ; 1,2), với x = 1,6 và y = 1,2 thì T = 250.1,6 + 160.1,2 = 592;

Tại C(1,6 ; 0,2), với x = 1,6 và y = 0,2 thì T = 250.1,6 + 160.0,2 = 432;

Tại D(0,6 ; 0,7), với x = 0,6 và y = 0,7 thì T = 250.0,6 + 160.0,7 = 262.

Giá trị nhỏ nhất của T là 248,25 đạt được khi (x ; y) = (0,225; 1,2).

Vậy gia đình cần mua 0,025 kg thịt bò và 1,2 kg thịt lợn.

Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1 trang 30 Toán lớp 10: Biểu diễn miền nghiệm của bất phương trình:....

Bài 2 trang 30 Toán lớp 10: Biểu diễn miền nghiệm của hệ bất phương trình:...

Bài 3 trang 30 Toán lớp 10: Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành trong một ngày là $1300$ mg. trong 1 lạng đậu nành có 165 mg canxi, 1 lạng thịt có 15 mg canxi....

Bài 5 trang 30 Toán lớp 10: Một chuỗi nhà hàng ăn nhanh bán đồ ăn từ 10h00 sáng đến 22h00 mỗi ngày....

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai