Với giải Luyện tập vận dụng 1 trang 48 Toán lớp 7 Cánh diều chi tiết trong Bài 4: Làm tròn và ước lượng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 4: Làm tròn và ước lượng
Luyện tập vận dụng 1 trang 48 Toán lớp 7: Quãng đường từ sân vận động Old Trafford ở Greater Manchester đến tháp đồng hồ Big Ben ở London (Vương Quốc Anh) khoảng 200 dặm. (Nguồn: https://www.google.com/maps). Tính độ dài quãng đường đó theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng đơn vị), biết 1 dặm = 1,609344 km.
Lời giải:
Quãng đường từ sân vận động Old Trafford ở Greater Manchester đến tháp đồng hồ Big Ben ở London (Vương Quốc Anh) theo đơn vị ki-lô-mét là khoảng:
200 . 1,609344 = 321,8688 ≈ 322 (km).
Vậy quãng đường đó dài khoảng 322 km.
Lý thuyết Làm tròn số
1.1 Số làm tròn
Ở nhiều tình huống thực tiễn ta cần tìm một số thực khác xấp xỉ với số thực đã cho để thuận tiện hơn trong ghi nhớ, đo đạc, hay tính toán. Số thực tìm được như thế được gọi là số làm tròn của số thực đã cho.
Ví dụ:
Hóa đơn tiền điện của gia đình bạn An tháng 9/2021 là 356 870 đồng. Trên thực tế mẹ của An đã trả tiền mặt cho người thu tiền điện 357 000 đồng.
Vậy số 357 000 là số làm tròn của số 356 870.
1.2 Làm tròn số với độ chính xác cho trước
Ta nói số a được làm tròn đến số b với độ chính xác d nếu khoảng cách giữa điểm a và điểm b trên trục số không vượt quá d.
Ví dụ: Làm tròn số 126 đến hàng chục ta được số 130. Khoảng cách giữa hai điểm 126 và 130 trên trục số là 130 – 126 = 4. Khoảng cách này không vượt quá 5. Khi đó ta nói số 126 được làm tròn đến số 130 với độ chính xác 5.
Nhận xét:
- Khi làm tròn số đến một hàng nào đó thì độ chính xác bằng nửa đơn vị của hàng làm tròn.
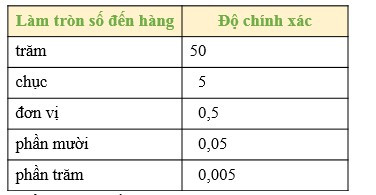
- Để làm tròn số với độ chính xác cho trước, ta có thể sử dụng cách ở bảng sau:
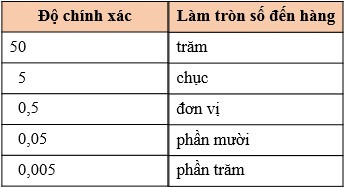
- Để làm tròn một số thập phân âm, ta chỉ cần làm tròn số đối của nó rồi đặt dấu “–” trước kết quả.
Ví dụ:
a) Làm tròn số 3,141592653… đến hàng phần trăm.
b) Làm tròn số 128,25 với độ chính xác 0,05.
c) Làm tròn số – 1,9254 với độ chính xác 0,005.
d) Làm tròn số với độ chính xác 0,5.
Hướng dẫn giải
a) Ta áp dụng quy tắc làm tròn số thập phân hữu hạn. Do chữ số ở hàng phần nghìn là 1 < 5 nên 3,141592653… ≈ 3,14.
Người ta chứng minh được rằng số 3,141592653… làm tròn đến 3,14 cũng với độ chính xác 0,005.
b) Để làm tròn số 128,25 với độ chính xác 0,05 ta sẽ làm tròn đến hàng phần mười. Áp dụng quy tắc làm tròn số ta được 128,25 ≈ 128,3.
c) Để làm tròn số –1,9254 với độ chính xác 0,005 ta sẽ làm tròn đến hàng phần trăm. Áp dụng quy tắc làm tròn số ta được 1,9254 ≈ 1,93. Vì vậy, – 1,9254 ≈ –1,93.
d)
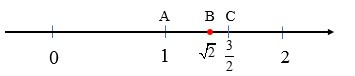
Ta biểu diễn số trên trục số. Khi đó AC = 0,5, điểm B nằm giữa A và C nên AB < AC.
Mà AC = 0,5 nên AB < 0,5, tức là khoảng cách giữa điểm và điểm 1 trên trục số nhỏ hơn 0,5. Vậy với độ chính xác 0,5 thì ≈ 1.
Chú ý: Trong đo đạc và tính toán thực tiễn, ta thường có gắng làm tròn số thực với độ chính xác d nhỏ nhất càng tốt. Trong thực tế, làm tròn số thực là một công việc có nhiều khó khăn. Tuy nhiên, người ta cũng biết một số cách để làm tròn số thực.
Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:
Câu hỏi khởi động trang 48 Toán lớp 7: Một bồn hoa có dạng hình tròn với bán kính là 0,8 m...
Luyện tập vận dụng 2 trang 49 Toán lớp 7: a) Làm tròn số 23 615 với độ chính xác 5
Bài 1 trang 51 Toán lớp 7: Làm tròn số 98 176 244 với độ chính xác 50
Bài 2 trang 51 Toán lớp 7: a) Làm tròn số 4,76908 với độ chính xác 0,5...
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Bài 3: Giá trị tuyệt đối của một số thực
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
