Với giải sách bài tập Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Giải SBT Toán 10 trang 79 Tập 1

Bài 12 trang 79 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 6,5 cm,  AC = 8,5 cm, $\widehat{A}=125°$. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).

a) Độ dài cạnh BC;

b) Số đo các góc B, C;

c) Diện tích tam giác ABC.

Lời giải:

a) Xét tam giác ABC, có:

BC² = AB² + AC² – 2.AB.AC.cosA

⇔ BC² = 6,5² + 8,5² – 2.6,5.8,5.cos125°

⇔ BC² ≈ 177,9

⇔ BC ≈ 13,3.

 Vậy BC ≈ 13,3.

b) Xét tam giác ABC, có:

$$\begin{gathered} \cos B=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC} \\ =\frac{6,5^2+13,3^2-8,5^2}{2.6,5.13,3}\approx 0,8 \end{gathered}$$

⇒ $\widehat{B}\approx 31,8°$

Ta lại có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc)

$$\begin{gathered} \Rightarrow \widehat{C}=180°-\left(\widehat{A}+\widehat{B}\right) \\ \approx 180°-\left(125°+31,8°\right)=23,2° \end{gathered}$$

Vậy $\widehat{B}\approx 31,8°$ và $\widehat{C}\approx 23,2°$.

c) Diện tích tam giác ABC là:

S = $\frac{1}{2}.AB.AC.\sin A$$=\frac{1}{2}.6,5.8,5.\sin 125°\approx 22,6$ (đvdt).

Vậy diện tích tam giác ABC là 22,6 đvdt.

Bài 13 trang 79 SBT Toán 10 Tập 1: Cho tam giác ABC có BC = 50 cm, $\widehat{B}=65°,\widehat{C}=45°$. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).

a) Độ dài cạnh AB, AC;

b) Bán kính đường tròn ngoài tiếp tam giác ABC.

Lời giải:

a) Xét tam giác ABC, có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc)

$$\begin{gathered} \Rightarrow \widehat{A}=180°-\left(\widehat{B}+\widehat{C}\right) \\ =180°-\left(65°+45°\right)=70° \end{gathered}$$

Áp dụng định lí sin trong tam giác ABC, ta được:

$\frac{AB}{\sin C}=\frac{AC}{\sin B}=\frac{BC}{\sin A}$

⇔ $\frac{AB}{\sin 45°}=\frac{AC}{\sin 65°}=\frac{50}{\sin 70°}=2R$

⇒ $\frac{AB}{\sin 45°}=\frac{50}{\sin 70°}$ ⇔ $AB=\frac{50.\sin 45°}{\sin 70°}\approx 37,6$

⇒ $\frac{AC}{\sin 65°}=\frac{50}{\sin 70°}$ ⇔ $AC=\frac{50\sin 65°}{\sin 70°}\approx 48,2$

Vậy AB ≈ 37,6 vậy AC ≈ 48,2.

b) Áp đụng định lí sin trong tam giác ABC, ta được:

$$\begin{gathered} \frac{BC}{\sin A}=2R\iff \frac{50}{\sin 70°}=2R \\ \iff R=\frac{50}{2\sin 70°}\approx 26,6 \end{gathered}$$

Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 26,6.

Bài 14 trang 79 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 5, AC = 8, BC = 9. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).

a) Số đo các góc A, B, C;

b) Diện tích tam giác ABC.

Lời giải:

a) Xét tam giác ABC, có:

Áp đụng hệ quả của định lí cos ta được:

$$\begin{gathered} \cos A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC} \\ =\frac{5^2+8^2-9^2}{\mathrm{2.5.8}}=\frac{1}{10} \\ \Rightarrow \widehat{A}\approx 84,3°; \end{gathered}$$

$$\begin{gathered} \cos B=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC} \\ =\frac{5^2+9^2-8^2}{\mathrm{2.5.9}}=\frac{7}{15} \\ \Rightarrow \widehat{B}\approx 62,2°; \end{gathered}$$

$$\begin{gathered} \cos C=\frac{A{C}^2+B{C}^2-A{B}^2}{2.BC.AC} \\ =\frac{8^2+9^2-5^2}{\mathrm{2.8.9}}=\frac{5}{6} \\ \Rightarrow \widehat{C}\approx 33,5°; \end{gathered}$$

Vậy $\widehat{A}\approx 84,3°,\widehat{B}\approx 62,2°,\widehat{C}\approx 33,5°$.

b) Diện tích tam giác ABC là:

$S=\frac{1}{2}AB.AC.\sin A$$\approx \frac{1}{2}\mathrm{.5.8.}\sin 84,3°\approx 19,9$ (đvdt).

Vậy diện tích tam giác là 19,9 đvdt.

Bài 15 trang 79 SBT Toán 10 Tập 1: Cho tam giác ABC có $\widehat{B}=60°$; BC = 8, AB + AC = 12. Tính độ dài các cạnh AB, AC.

Lời giải:

Đặt AB = x (x > 0)

Ta có AB + AC = 12 ⇒ AC = 12 – AB = 12 – x

Xét tam giác ABC, ta có:

AC² = AB² + BC² – 2.AB.BC.cosB

⇔ (12 – x)² = x² + 8² – 2.x.8.cos60°

⇔ 144 – 24x + x² = x² + 64 – 8x

⇔ – 16x = – 80

⇔ x = 5

⇒ 12 – x = 12 – 5 = 7

Vậy AB = 5cm, AC = 7cm.

Bài 16 trang 79 SBT Toán 10 Tập 1: Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m, chiều dài của hàng rào MP là 230 m. Góc giữa hai hàng rào MN và MP là 110° (Hình 21).

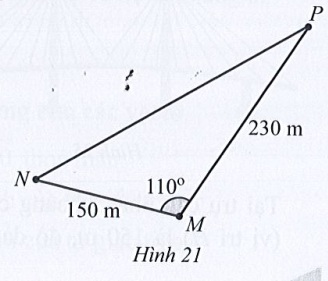
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?

b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười).

Lời giải:

a) Diện tích mảnh đất gia đình An bằng diện tích hình tam giác MNP và bằng:

$$\begin{gathered} S=\frac{1}{2}.MN.MP.\sin M \\ =\frac{1}{2}\mathrm{.150.230.}\sin 110° \\ =16209,7 \left(m^2\right) \end{gathered}$$

Vậy diện tích mảnh đất gia đình An là 16 209,7 m².

b) Xét tam giác MNP, có:

NP² = MN² + MP² – 2.MN.MP.cosM

⇔ NP² = 150² + 230² – 2.150.230.cos110°

⇔ NP² = 150² + 230² – 2.150.230.cos110°

⇔ NP² ≈ 98 999,4

⇔ NP ≈ 314,6

Vậy hàng rào NP dài 314,6 mét.

Giải SBT Toán 10 trang 80 Tập 1

Bài 17 trang 80 SBT Toán 10 Tập 1: Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB = 100m. Hai người tiến hành đo đạc và thu được kết quả $\widehat{CAB}=54°,\widehat{CBA}=74°$(Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?

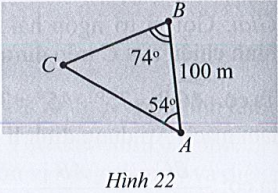
Lời giải:

Xét tam giác ABC, có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc) $$\begin{gathered} \Rightarrow \widehat{C}=180°-\left(\widehat{A}+\widehat{B}\right) \\ =180°-\left(54°+74°\right)=52° \end{gathered}$$.

Áp dụng định lí sin, ta được:

$\frac{BC}{\sin A}=\frac{AB}{\sin C}$

⇔ $\frac{BC}{\sin 54°}=\frac{100}{\sin 52°}$

⇔ $BC=\frac{100.\sin 54°}{\sin 52°}\approx 102,7$.

Vậy con tàu cách đảo 102, 7 m.

Bài 18 trang 80 SBT Toán 10 Tập 1: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: AB = 30 m, $\widehat{CAB}=60°,\widehat{CBA}=50°$ (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

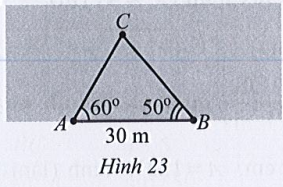
Lời giải:

Xét tam giác ABC, có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc)

$$\begin{gathered} \Rightarrow \widehat{C}=180°-\left(\widehat{A}+\widehat{B}\right) \\ =180°-\left(60°+50°\right)=70° \end{gathered}$$

Áp dụng định lí sin, ta được:

$\frac{AB}{\sin C}=\frac{AC}{\sin B}$

⇔ $\frac{30}{\sin 70°}=\frac{AC}{\sin 50°}$

⇔ $AC=\frac{30.\sin 50°}{\sin 70°}\approx 24,5$

Vậy khoảng cách từ vị trí A đến con tàu C là 24,5 m.

Bài 19 trang 80 SBT Toán 10 Tập 1: Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m,

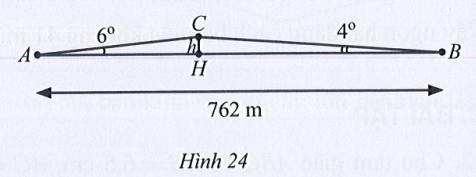
a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng vận tốc trung bình lên dốc là 4km/h và tốc độ khi xuống dốc là 19 km/h.

Lời giải:

a) Đặt AH = x (m) (x > 0)

⇒ BH = AB – AH = 762 – x (m)

Xét tam giác AHC vuông tại H, có:

$\tan A=\frac{CH}{AH}$

⇔ $\tan 6°=\frac{CH}{x}$

⇔ CH = tan6°.x

Xét tam giác BHC vuông tại H, có:

$\tan B=\frac{CH}{BH}$

⇔ $\tan 4°=\frac{CH}{762-x}$

⇔ CH = tan4°.(762 – x)

⇒ tan6°.x = tan4°.(762 – x)

⇔ (tan6° + tan4°).x ≈ 53,3

⇔ x ≈ 304,4

⇒ CH ≈ tan6°.304,4 ≈ 32

Vậy chiều cao của con dốc là 32 m.

b) Xét tam giác AHC vuông tại H, có:

$sinA=\frac{CH}{AC}$

⇔ $sin6°=\frac{32}{AC}$

⇔ AC = $\frac{32}{\sin 6°}\approx 306,1m=0,3061km.$

Xét tam giác BHC vuông tại H, có:

$sinB=\frac{CH}{CB}$

⇔ $\sin 4°=\frac{32}{AB}$

$\iff AB=\frac{32}{\sin 4°}\approx 458,7m$$=0,4587km.$

Thời gian bạn AN đi từ nhà đến trường là: $\frac{0,3061}{4}+\frac{0,4587}{19}\approx 0,1$ (giờ) = 6 phút.

Vậy bạn An đến trường lúc: 6 giờ 6 phút.

Bài 20 trang 80 SBT Toán 10 Tập 1: Quan sát cây cầu văng minh họa ở Hình 25.

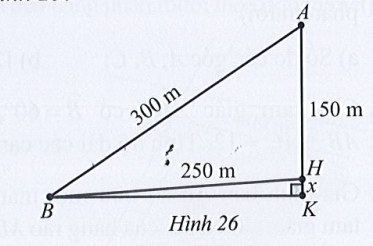
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Lời giải:

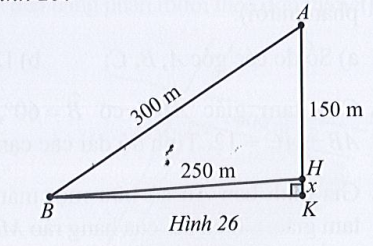
Xét tam giác ABC, có:

$$\begin{gathered} \text{cos}\widehat{AHB}=\frac{A{H}^2+B{H}^2-A{B}^2}{2.AH.BH} \\ =\frac{{150}^2+{250}^2-{300}^2}{\mathrm{2.150.250}}=-\frac{1}{15} \end{gathered}$$

⇒ $\widehat{AHB}\approx 93,8°$

Ta lại có: $\widehat{AHB}+\widehat{BHK}=180°$

$$\begin{gathered} \widehat{BHK}=180°-\widehat{AHB} \\ =180°-93,8°=86,2° \end{gathered}$$

Xét tam giác BHK vuông tại K, có:

$\widehat{HBK}+\widehat{BHK}=90°$ (hai góc phụ nhau)

⇔ $\widehat{HBK}=90°-\widehat{BHK}$

⇔ $\widehat{HBK}\approx 90°-86,2°=3,8°$.

Vậy độ dốc của cầu qua trụ khoảng 3,8°.

Giải SBT Toán 10 trang 81 Tập 1

Bài 21 trang 81 SBT Toán 10 Tập 1: Một người đứng ở vị trí A trên nóc của một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20 m và đo được $\widehat{BAC}=45°$(Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

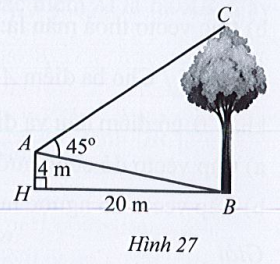
Lời giải:

Xét tám giác vuông AHB, có:

AB² = AH² + HB² (định lí pythagoras)

⇔ AB² = 4² + 20²

⇔ AB² = 416

⇔ AB ≈ 20,4

Ta lại có: $\tan \widehat{HAB}=\frac{HB}{HA}$ ⇔ $\tan \widehat{HAB}=\frac{20}{4}=5$$\Rightarrow \widehat{HAB}\approx 78,7°$

Ta có: AH ⊥ BH và CB ⊥ BH nên AH // CB

⇒ $\widehat{HAB}=\widehat{ABC}\approx 78,7°$ (hai góc so le trong)

Xét tam giác ABC có:

$$\begin{gathered} \widehat{C}=180°-\widehat{BAC}-\widehat{ABC} \\ =180°-45°-78,7°=56,3^o \end{gathered}$$

Áp dụng định lí sin trong tam giác ta được:

$\frac{BC}{\sin A}=\frac{AB}{\sin C}$

⇔ $BC=\frac{AB\sin A}{\sin C}=\frac{20,4.\sin 45°}{\sin 56,3°}\approx 17,3$.

Vậy chiều cao của cây là 17,3 m.

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài 1: Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180°

Bài 3: Khái niệm vectơ

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ

Lý thuyết Giải tam giác. Tính diện tích tam giác

1. Giải tam giác

Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:

– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;

– Biết độ dài ba cạnh;

– Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

Ví dụ: Cho tam giác ABC có AB = 4, BC = 6, AC = $2\sqrt{7}$. Điểm M thuộc đoạn BC sao cho MC = 2MB.

a) Tính cos các góc của tam giác ABC.

b) Tính độ dài cạnh AM.

Hướng dẫn giải:

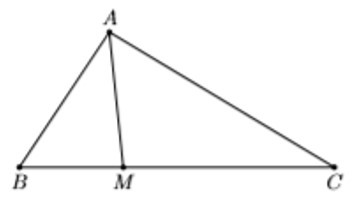
a) Theo định lí cosin trong tam giác ABC ta có:

cosB = $\frac{{\mathrm{AB}}^2+{\mathrm{BC}}^2-{\mathrm{AC}}^2}{2\mathrm{AB}.\mathrm{BC}}$= $\frac{4^2+6^2-{\left(2\sqrt{7}\right)}^2}{\mathrm{2.4.6}}$= $\frac{1}{2}$

⇒ $\widehat{\mathrm{B}}$= 60°.

cosC = $\frac{{\mathrm{AC}}^2+{\mathrm{BC}}^2-{\mathrm{AB}}^2}{2\mathrm{AC}.\mathrm{BC}}$= $\frac{{\left(2\sqrt{7}\right)}^2+6^2-4^2}{2.2\sqrt{7}.6}$= $\frac{2\sqrt{7}}{7}$

cosA = $\frac{{\mathrm{AB}}^2+{\mathrm{AC}}^2-{\mathrm{BC}}^2}{2\mathrm{AB}.\mathrm{AC}}$= $\frac{4^2+{\left(2\sqrt{7}\right)}^2-6^2}{\mathrm{2.4.2}\sqrt{7}}$= $\frac{\sqrt{7}}{14}$

b) Ta có:

MC = 2MB ⇒ $\frac{\mathrm{MB}}{\mathrm{MC}}$= $\frac{1}{2}$⇒ $\frac{\mathrm{MB}}{\mathrm{BC}}$= $\frac{1}{3}$

⇒ MB = $\frac{1}{3}$BC = $\frac{1}{3}$.6 = 2

Áp dụng định lí côsin trong tam giác AMB ta có:

AM² = AB² + BM² – 2AB.BM.cosB = 4² + 2² – 2.4.2. $\frac{1}{2}$= 12

⇒ AM = $\sqrt{12}$= $2\sqrt{3}$

Ví dụ: Cho tam giác ABC có $\widehat{\mathrm{B}}=35°$; $\widehat{\mathrm{C}}=50°$ và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).

Hướng dẫn giải:

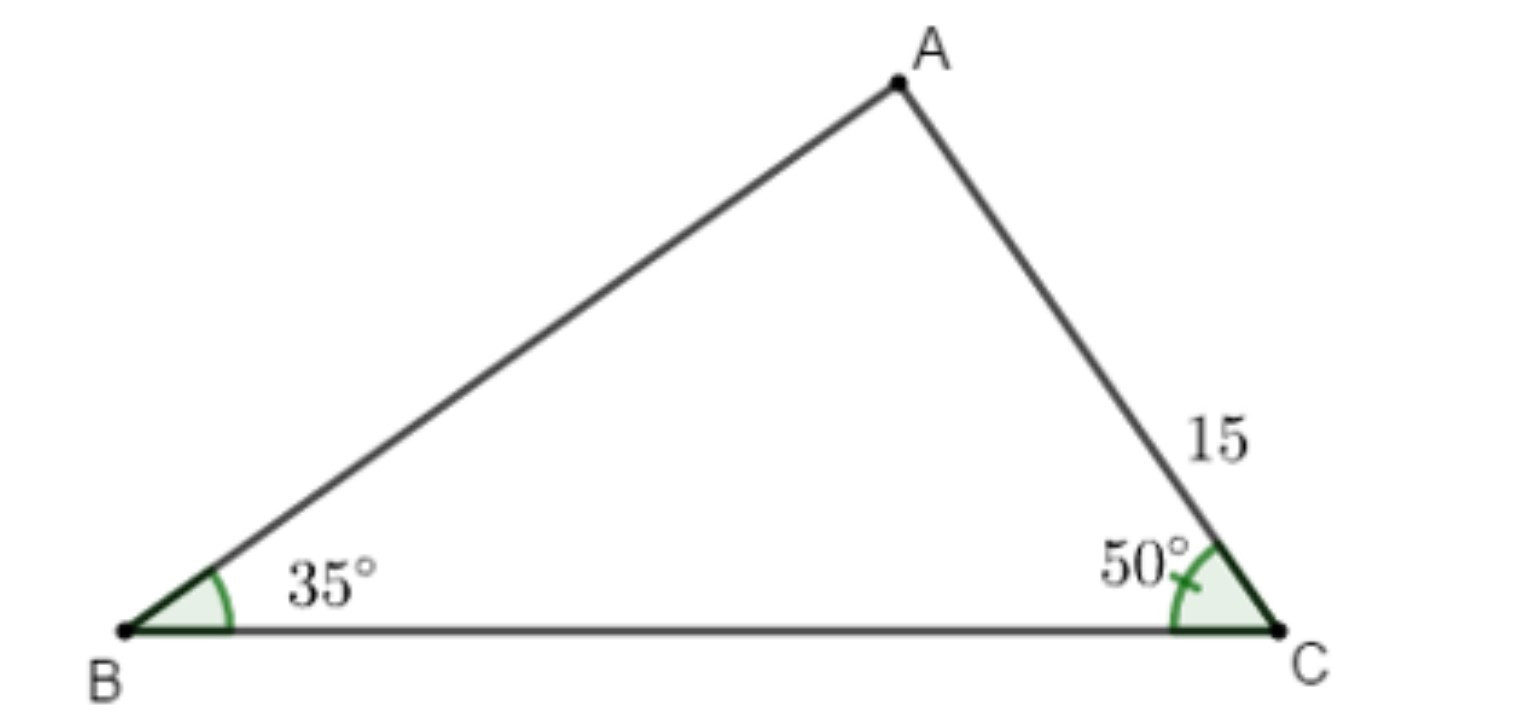
Ta có:

$\widehat{\mathrm{A}}$ + $\widehat{\mathrm{B}}$ + $\widehat{\mathrm{C}}$= 180° (tổng ba góc trong tam giác)

Suy ra:

$\widehat{\mathrm{A}}$ = 180° – $\widehat{\mathrm{B}}$ – $\widehat{\mathrm{C}}$ = 180° – 35° – 50° = 95°

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{\mathrm{BC}}{\mathrm{sinA}}$ = $\frac{\mathrm{AC}}{\mathrm{sinB}}$ = $\frac{\mathrm{AB}}{\mathrm{sinC}}$

Suy ra:

BC = $\frac{\mathrm{AC}.\mathrm{sinA}}{\mathrm{sinB}}$= $\frac{15.\sin 95°}{\sin 35°}$≈ 26,05cm

AB = $\frac{\mathrm{AC}.\mathrm{sinC}}{\mathrm{sinB}}$= $\frac{15.\sin 50°}{\sin 35°}$≈ 20,03cm

Vậy BC = 26,05cm và AB ≈ 20,03 cm.

2. Tính diện tích tam giác

Công thức tính diện tích tam giác:

• Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:

S = $\frac{1}{2}$bc.sinA = $\frac{1}{2}$ca.sin = $\frac{1}{2}$ab.sinC

Ví dụ: Cho tam giác ABC có BC = $4\sqrt{2}$, $\widehat{\mathrm{A}}$= 45°, $\widehat{\mathrm{B}}$= 120°. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Ta có:

$\widehat{\mathrm{A}}$ + $\widehat{\mathrm{B}}$ + $\widehat{\mathrm{C}}$= 180° (tổng ba góc trong tam giác)

Suy ra: $\widehat{\mathrm{C}}$= 180° – $\widehat{\mathrm{A}}$ – $\widehat{\mathrm{B}}$ = 180° – 45° – 120° = 15°

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{\mathrm{BC}}{\mathrm{sinA}}$ = $\frac{\mathrm{AC}}{\mathrm{sinB}}$ = $\frac{\mathrm{AB}}{\mathrm{sinC}}$

Suy ra:

AC = $\frac{\mathrm{BC}.\mathrm{sinB}}{\mathrm{sinA}}$ = $\frac{4\sqrt{2}.\sin 120°}{\sin 45°}$ = $4\sqrt{3}$;

AB = $\frac{\mathrm{AC}.\mathrm{sinC}}{\mathrm{sinB}}$= $\frac{4\sqrt{3}.\sin 15°}{\sin 120°}$ = $2\sqrt{6}-2\sqrt{2}$;

Diện tích tam giác ABC là:

S = $\frac{1}{2}$AC.AB.sinA = $\frac{1}{2}.4\sqrt{3}.(2\sqrt{6}-2\sqrt{2}).\sin 45°$ = $12-4\sqrt{3}$(đơn vị diện tích).

• Công thức Heron:

Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$. Khi đó, diện tích S của tam giác ABC là:

$\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$.

Trong đó p là nửa chu vi tam giác ABC.

Ví dụ: Chứng minh công thức Heron.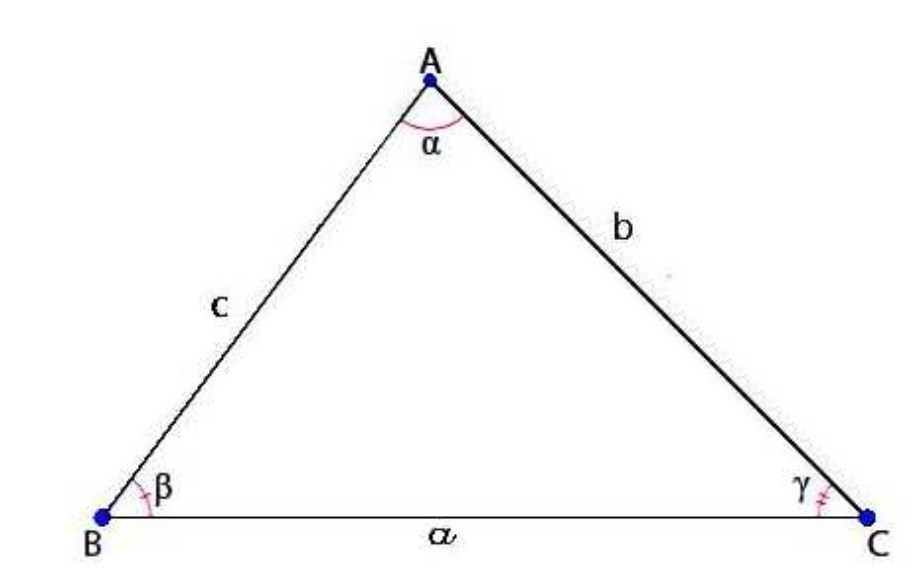

Hướng dẫn giải:

Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh. Theo hệ quả định lý cosin, ta có:

cosC = $\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}$.

Mà:

sin²C + cos²C = 1

⇒ sinC = $\sqrt{1-{\cos }^2\mathrm{C}}$= $\sqrt{1-{\left(\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}\right)}^2}$= $\frac{\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}}{2\mathrm{ab}}$

Ta có công thức tính diện tích tam giác ABC:

S = $\frac{1}{2}$absinC

   = $\frac{1}{2}$ab. $\frac{\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}}{2\mathrm{ab}}$

   = $\frac{1}{4}$$\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}$

   = $\frac{1}{4}\sqrt{(2\mathrm{ab}-({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2\left)\right)(2\mathrm{ab}+({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2\left)\right)}$

   = $\frac{1}{4}\sqrt{({\mathrm{c}}^2-{(\mathrm{a}-\mathrm{b})}^2)({(\mathrm{a}+\mathrm{b})}^2-{\mathrm{c}}^2)}$

   = $\frac{1}{4}\sqrt{(\mathrm{c}-(\mathrm{a}-\mathrm{b}\left)\right)(\mathrm{c}+(\mathrm{a}-\mathrm{b}\left)\right)\left(\right(\mathrm{a}+\mathrm{b})-\mathrm{c})\left(\right(\mathrm{a}+\mathrm{b})+\mathrm{c})}$

   = $\frac{1}{4}\sqrt{(\mathrm{a}+\mathrm{b}+\mathrm{c})(\mathrm{c}-\mathrm{a}+\mathrm{b})(\mathrm{c}+\mathrm{a}-\mathrm{b})(\mathrm{a}+\mathrm{b}-\mathrm{c})}$

   = $\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{a}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{b}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{c})$

   = $\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$

Với $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$.

Suy ra $\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$ (đpcm).

Ví dụ: Cho tam giác ABC có BC = 9, CA = 6, AB = 5. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Nửa chu vi tam giác ABC là:

$\mathrm{p}=\frac{\mathrm{AB}+\mathrm{AC}+\mathrm{BC}}{2}$= $\frac{5+6+9}{2}$= 10

Áp dụng công thức Heron, diện tích tam giác ABC là:

$\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{AB})(\mathrm{p}-\mathrm{AC})(\mathrm{p}-\mathrm{BC})}$= $\sqrt{10(10-5)(10-6)(10-9)}$= $10\sqrt{2}$(đvdt)

3. Áp dụng vào bài toán thực tiễn

Trong thực tiễn, ta có thể áp dụng hệ thức lượng trong tam giác vào các bài toán như tính khoảng cách giữa hai vị trí, tính diện tích,... giúp cho việc tính toán trở nên chính xác và nhanh chóng hơn. Chúng ta có thể xem ví dụ sau:

Ví dụ: Đường dây cao thế nối thẳng từ vị trí A đến vị trí B dài 10 km, từ vị trí A đến vị trí C dài 8 km, góc tạo bởi hai đường dây trên bằng 75°. Tính khoảng cách từ vị trí B đến vị trí C (làm tròn đến chữ số thập phân thứ 2).

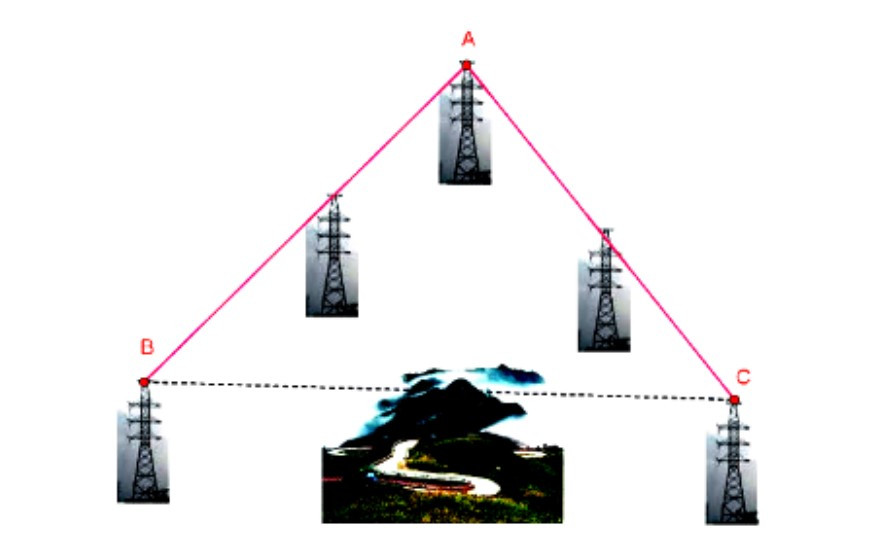
Hướng dẫn giải:

Áp dụng định lí cosin vào tam giác ABC ta có:

BC² = AB² + AC² – 2AB.AC.cosA = 8² + 10² – 2.8.10.cos75° $\approx$ 122,59

BC $\approx$ 11,07

Vậy khoảng cách từ B đến C là khoảng 11,07 km.