Với giải sách bài tập Toán 10 Bài tập cuối chương 6 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài tập cuối chương 6
Giải SBT Toán 10 trang 131 Tập 1
A. TRẮC NGHIỆM
Bài 1 trang 131 SBT Toán 10 Tập 1: Số quy tròn của 45,6534 với độ chính xác d = 0,01 là:
A. 45,65;
B. 45,6;
C. 45,7;
D. 45.
Lời giải:
Đáp án đúng là: C
Xét d = 0,01 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần trăm. Nên suy ra hàng lớn nhất của độ chính xác d = 0,01 là hàng phần trăm nên ta quy tròn số 45,6534 ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần mười.
Xét chữ số ở hàng phần trăm của 45,6534 là 5, nên ta suy ra được số quy tròn của 45,6534 đến hàng phần mười là 45,7.
Bài 2 trang 131 SBT Toán 10 Tập 1: Cho biết Số gần đúng của với độ chính xác 0,0001 là:
A. 1,4422;
B. 1,4421;
C. 1,442;
D. 1,44.
Lời giải:
Đáp án đúng là: A
Xét d = 0,0001 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần chục nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,0001 là hàng phần chục nghìn nên ta quy tròn số ở hàng vừa tìm được, tức là hàng phần chục nghìn.
Xét chữ số ở hàng phần trăm nghìn của là 4, là số bé hơn 5 nên ta suy ra được số gần đúng của với độ chính xác d = 0,0001 là 1,4422.
A. 0,16;
B. 0,15;
C. 0,157;
D. 0,159.
Lời giải:
Đáp án đúng là: A
Xét d = 0,002 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,002 là hàng phần nghìn nên ta quy tròn số a ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần trăm.
Xét chữ số ở hàng phần nghìn của a là 7, là số lớn hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần trăm là 0,16.
A. 32 cm;
B. 32 ± 0,2 cm;
C. 64 ± 0,8 cm;
D. 32 ± 0,8 cm.
Lời giải:
Đáp án đúng là: D
Độ dài cạnh của một hình vuông là 8 ± 0,2 cm thì chu vi của hình vuông đó bằng: p = 4.(8 ± 0,2) = 32 ± 0,8 cm.
Bài 5 trang 131 SBT Toán 10 Tập 1: Trung vị của mẫu số liệu 4; 6; 7; 6; 5; 4; 5 là:
A. 4;
B. 5;
C. 6;
D. 7.
Lời giải:
Đáp án đúng là: B
Ta có: n = 7
Sắp xếp dãy số liệu theo thứ tự không giảm là: 4; 4; 5; 5; 6; 6; 7.
Vì n = 7 là số lẻ nên số trung vị của mẫu số liệu ở trên là: Me = 5.
A. 3;
B. 4;
C. 5;
D. 6.
Lời giải:
Đáp án đúng là: C
Ta có: n = 12
Sắp xếp dãy số liệu theo thứ tự không giảm là:
4; 5; 5; 6; 6; 6; 6; 7; 7; 7; 9; 9
Khi đó, khoảng biến thiên R = 9 – 4 = 5.
Bài 7 trang 131 SBT Toán 10 Tập 1: Tứ phân vị thứ nhất của mẫu số liệu 2; 4; 5; 6; 6; 7; 3; 4 là:
A. 3;
B. 3,5;
C. 4;
D. 4,5.
Lời giải:
Đáp án đúng là: B
Ta có: n = 8
Sắp xếp dãy số liệu theo thứ tự không giảm là: 2; 3; 4; 4; 5; 6; 6; 7
Vì n = 8 là số chẵn nên ta có tứ phân vị thứ hai Q2 = (4 + 5) : 2 = 4,5.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 2; 3; 4; 4.
Vậy Q1 = (3 + 4) : 2 = 3,5.
Bài 8 trang 131 SBT Toán 10 Tập 1: Khoảng tứ phân vị của mẫu số liệu 4; 7; 5; 6; 6; 7; 9; 5; 6 là:
A. 1;
B. 1,5;
C. 2;
D. 2,5.
Lời giải:
Đáp án đúng là: C
Ta có: n = 9
Sắp xếp dãy số liệu theo thứ tự không giảm là: 4; 5; 5; 6; 6; 6; 7; 7; 9
Vì n = 9 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 6.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 4; 5; 5; 6.
Vậy Q1 = (5 + 5) : 2 = 5.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 6; 7; 7; 9.
Vậy Q3 = (7 + 7) : 2 = 7.
Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 7 – 5 = 2.
Bài 9 trang 131 SBT Toán 10 Tập 1: Dãy số liệu 5; 6; 0; 3; 5; 10; 3; 4 có các giá trị ngoại lệ là:
A. 0;
B. 10;
C. 0; 10;
D. ∅.
Lời giải:
Đáp án đúng là: B
Ta có: n = 8
Sắp xếp dãy số liệu theo thứ tự không giảm là: 0; 3; 3; 4; 5; 5; 6; 10
Vì n = 8 là số chẵn nên ta có tứ phân vị thứ hai Q2 = (4 + 5) : 2 = 4,5.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 0; 3; 3; 4.
Vậy Q1 = (3 + 3) : 2 = 3.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 5; 5; 6; 10.
Vậy Q3 = (5 + 6) : 2 = 5,5.
Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 5,5 – 3 = 2,5.
Giá trị ngoại lệ x thỏa mãn
x > Q3 + 1,5∆Q = 5,5 + 1,5.2,5 = 9,25
Hoặc x < Q1 − 1,5∆Q = 3 − 1,5.2,5 = −0,75
Vậy đối chiếu mẫu số liệu suy ra giá trị ngoại lệ là 10.
Bài 10 trang 131 SBT Toán 10 Tập 1: Phương sai của dãy số liệu 4; 5; 0; 3; 3; 5; 6; 10 là:
A. 6,5;
B. 6,75;
C. 7;
D. 7,25.
Lời giải:
Đáp án đúng là: D
Ta có n = 8
Số trung bình của mẫu số liệu là
Khi đó phương sai của dãy số liệu là:
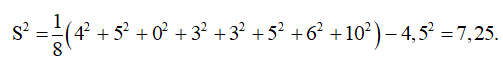
B. TỰ LUẬN
Bài 1 trang 131 SBT Toán 10 Tập 1: Viết số quy tròn của mỗi số sau với độ chính xác d:
a) a = −0,4356217 với d = 0,0001;
Lời giải:
a) Xét d = 0,0001 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần chục nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,0001 là hàng chục nghìn nên ta quy tròn số a ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần nghìn.
Xét chữ số ở hàng phần chục nghìn của a là 6, lớn hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần nghìn là −0,436.
b) Xét d = 0,001 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,001 là hàng phần nghìn nên ta quy tròn số b ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần trăm.
Xét chữ số ở hàng phần nghìn của b là 4, là số bé hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần trăm là 0,20.
Lời giải:
Gọi và lần lượt là bán kính và chu vi của hình tròn.
Ta có = 5 ± 0,2 nên suy ra 4,8 ≤ ≤ 5,2.
Mà 3,141 < π < 3,142 nên suy ra:
2 . 4,8 . 3,141 ≤ 2.. π ≤ 2. 5,2 . 3,142
⇔ 30,1536 ≤ ≤ 32,6768.
Ta có: p = 31,4 là số gần đúng của nên sai số tuyệt đối của số gần đúng p là ∆p = | − 31,4|.
Mà 30,1536 ≤ ≤ 32,6768
⇔ 30,1536 − 31,4 ≤ − 31,4 ≤ 32,6768 − 31,4
⇔ −1,2464 ≤ − 31,4 ≤ 1,2768
⇒ | − 31,4| ≤ 1,2768.
Vậy suy ra sai số tuyệt đối của p là ∆p = | − 31,4| ≤ 1,2768.
Giải SBT Toán 10 trang 132 Tập 1

a) Sử dụng số trung bình và trung vị, hãy so sánh số sách mà mỗi học sinh tổ 1 và tổ 2 quyên góp được cho thư viện trường.
Lời giải:
a) Mỗi tổ có 12 học sinh quyên góp, n = 12.
+) Tổ 1:
Sắp xếp mẫu số liệu theo thứ tự không giảm
1; 6; 6; 6; 6; 7; 7; 9; 9; 9; 9; 10
Trung bình số sách mà tổ 1 quyên góp là
Với n = 12 là số chẵn nên số trung vị của mẫu số liệu của tổ 1 là
Me = (7 + 7) : 2 = 7.
Khi đó tứ phân vị thứ hai là Q2 = 7.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 1; 6; 6; 6; 6; 7.
Vậy Q1 = (6 + 6) : 2 = 6.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 7; 9; 9; 9; 9; 10.
Vậy Q3 = (9 + 9) : 2 = 9.
Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 9 – 6 = 3.
+) Tổ 2:
Sắp xếp mẫu số liệu theo thứ tự không giảm
5; 6; 7; 7; 7; 8; 8; 9; 9; 9; 10; 30
Trung bình số sách mà tổ 2 quyên góp là
Với n = 12 là số chẵn nên số trung vị của mẫu số liệu của tổ 2 là
Me = (8 + 8) : 2 = 8.
Khi đó tứ phân vị thứ hai là Q2 = 8.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 5; 6; 7; 7; 7; 8.
Vậy Q1 = (7 + 7) : 2 = 7.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 8; 9; 9; 9; 10; 30.
Vậy Q3 = (9 + 9) : 2 = 9.
Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 9 – 7 = 2.
Vậy nếu so sánh theo số trung bình và trung vị thì số sách các bạn tổ 2 quyên góp được nhiều hơn các bạn tổ 1.
b)
+) Tổ 1:
Giá trị ngoại lệ x thỏa mãn
x > Q3 + 1,5∆Q = 9 + 1,5.3 = 13,5
Hoặc x < Q1 − 1,5∆Q = 6 − 1,5.3 = 1,5
Vậy đối chiếu mẫu số liệu của tổ 1 suy ra giá trị ngoại lệ là 1.
+) Tổ 2:
Giá trị ngoại lệ x thỏa mãn
x > Q3 + 1,5∆Q = 9 + 1,5.2 = 12
Hoặc x < Q1 − 1,5∆Q = 7 − 1,5.2 = 4
Vậy đối chiếu mẫu số liệu của tổ 2 suy ra giá trị ngoại lệ là 30.
Sau khi bỏ đi các giá trị ngoại lệ này thì tổ 1 có:
Và số trung vị Me = 7 (Do n = 11 là số lẻ).
Tương tự thì tổ 2 có:
Và số trung vị Me = 8 (Do n = 11 là số lẻ).
Vậy sau khi bỏ các giá trị ngoại lệ thì khi so sánh theo số trung bình và trung vị các bạn tổ 2 vẫn quyên góp được nhiều sách hơn các bạn tổ 1.
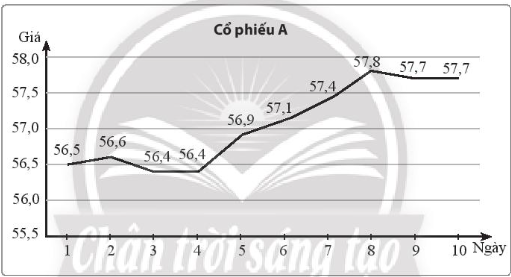
a) Viết mẫu số liệu thống kê giá của mã cổ phiếu A từ biểu đồ trên.
b) Tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu đó.
c) Tính số trung bình, độ lệch chuẩn của mẫu số liệu.
Lời giải:
a) Mẫu số liệu thống kê giá của mã cổ phiếu A từ biểu đồ trên là:
56,5; 56,6; 56,4; 56,4; 56,9; 57,1; 57,4; 57,8; 57,7; 57,7
b) Với n = 10
Sắp xếp mẫu số liệu theo chiều không giảm:
56,4; 56,4; 56,5; 56,6; 56,9; 57,1; 57,4; 57,7; 57,7; 57,8
Khi đó, khoảng biến thiên R = 57,8 – 56,4 = 1,4.
Vì n = 10 là số chẵn nên ta có tứ phân vị thứ hai
Q2 = (56,9 + 57,1) : 2 = 57.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 56,4; 56,4; 56,5; 56,6; 56,9.
Vậy Q1 = 56,5.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 57,1; 57,4; 57,7; 57,7; 57,8.
Vậy Q3 = 57,7.
Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 57,7 – 56,5 = 1,2.
c) Số trung bình của mẫu số liệu là
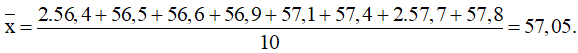
Phương sai:
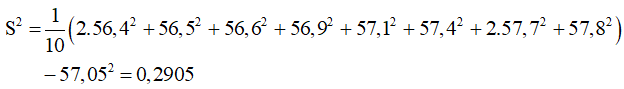
Khi đó độ lệch chuẩn S ≈ 0,54.
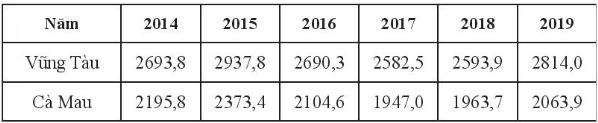
a) Sử dụng số trung bình, hãy so sánh số giờ nắng mỗi năm của Vũng Tàu và Cà Mau trong 6 năm trên.
b) Sử dụng số trung vị, hãy so sánh số giờ nắng mỗi năm của Vũng Tàu và Cà Mau trong 6 năm trên.
Lời giải:
a) Trung bình số giờ nắng mỗi năm tại Vũng Tàu là
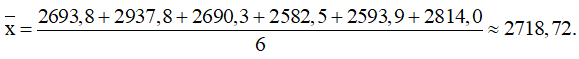
Trung bình số giờ nắng mỗi năm tại Cà Mau là
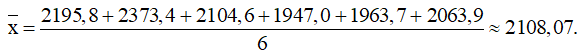
Do đó nếu sử dụng số trung bình thì thời gian nắng mỗi năm ở Vũng Tàu nhiều hơn ở Cà Mau.
b)
+) Sắp xếp mẫu số liệu của Vũng Tàu theo chiều không giảm:
2582,5; 2593,9; 2690,3; 2693,8; 2814,0; 2937,8
Vì n = 6 là số chẵn nên số trung vị của mẫu số liệu trên là
Me = (2690,3 + 2693,8) : 2 = 2692,05.
+) Sắp xếp mẫu số liệu của Cà Mau theo chiều không giảm:
1947,0; 1963,7; 2063,9; 2104,6; 2195,8; 2373,4
Vì n = 6 là số chẵn nên số trung vị của mẫu số liệu trên là
Me = (2063,9 + 2104,6) : 2 = 2084,25.
Do đó nếu sử dụng trung vị thì thời gian nắng mỗi năm ở Vũng Tàu nhiều hơn ở Cà Mau.
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu
Bài 1: Dấu của tam thức bậc hai
Bài 2: Giải bất phương trình bậc hai một ẩn
Bài 3: Phương trình quy về phương trình bậc hai
Lý thuyết Chương 6: Thống kê
1. Số gần đúng
Trong thực tế cuộc sống cũng như trong khoa học kĩ thuật, có nhiều đại lượng mà ta không thể xác định được giá trị chính xác. Mỗi dụng cụ hay phương pháp đo khác nhau có thể sẽ cho ra các kết quả khác nhau. Vì vậy kết quả thu được thường chỉ là những số gần đúng.
2. Sai số tuyệt đối và sai số tương đối
2.1. Sai số tuyệt đối
Nếu a là số gần đúng của số đúng thì được gọi là sai số tuyệt đối của số gần đúng a.
* Độ chính xác:
Trên thực tế ta thường không biết số đúng nên không thể tính được chính xác ∆a. Khi đó, ta thường tìm cách khống chế sai số tuyệt đối ∆a không vượt quá mức d > 0 cho trước:
hay a – d ≤ ≤ a + d.
Khi đó, ta nói a là số gần đúng của số đúng với độ chính xác d.
Quy ước viết gọn: .
2.2. Sai số tương đối
Sai số tương đối của số gần đúng a, kí hiệu là δa, là tỉ số giữa sai số tuyệt đối ∆a và |a|, tức là .
Nếu thì ∆a ≤ d. Do đó . Nếu δa hay càng nhỏ thì chất lượng của phép đo đạc hay tính toán càng cao.
Chú ý: Người ta thường viết sai số tương đối dưới dạng phần trăm.
3. Số quy tròn
3.1. Quy tắc làm tròn số
Quy tắc làm tròn số đến một hàng nào đó (gọi là hàng quy tròn):
+ Nếu chữ số sau hàng quy tròn nhỏ hơn 5 thì ta thay nó và các chữ số bên phải nó bởi chữ số 0.
+ Nếu chữ số sau hàng quy tròn lớn hơn hoặc bằng 5 thì ta cũng làm như trên nhưng cộng thêm 1 đơn vị vào chữ số hàng quy tròn.
Chú ý:
+ Khi thay số đúng bởi số quy tròn đến một hàng nào đó thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Ta có thể nói độ chính xác của số quy tròn bằng nửa đơn vị của hàng quy tròn.
+ Khi quy tròn số đúng đến một hàng nào đó thì ta nói số gần đúng a nhận được là chính xác đến hàng đó. Ví dụ số gần đúng của π chính xác đến hàng phần trăm là 3,14.
3.2. Xác định số quy tròn của số gần đúng với độ chính xác cho trước
Các bước xác định số quy tròn của số gần đúng a với độ chính xác d cho trước:
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.
Bước 2: Quy tròn số a ở hàng gấp 10 lần hàng tìm được ở Bước 1.
3.3. Xác định số gần đúng của một số với độ chính xác cho trước
Để tìm số gần đúng a của số đúng với độ chính xác d, ta thực hiện các bước sau:
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.
Bước 2: Quy tròn đến hàng tìm được ở trên.
4. Bảng số liệu
Dựa vào các thông tin đã biết và sử dụng mối liên hệ toán học giữa các số liệu, ta có thể phát hiện ra được số liệu không chính xác trong một số trường hợp.
5. Biểu đồ
Ta có thể biểu diễn số liệu thống kê dưới dạng biểu đồ.
Một số dạng biểu đồ thường gặp: biểu đồ cột, biểu đồ cột kép, biểu đồ quạt, biểu đồ tranh,…
Quan sát các biểu đồ ta có thể đưa ra các nhận xét về số liệu thống kê.
6. Số trung bình
6.1. Công thức tính số trung bình
• Giả sử ta có một mẫu số liệu là x1, x2, …, xn.
Số trung bình (hay số trung bình cộng) của mẫu số liệu này, kí hiệu là , được tính bởi công thức
.
• Giả sử mẫu số liệu được cho dưới dạng bảng tần số
|
Giá trị |
x1 |
x2 |
… |
xk |
|
Tần số |
n1 |
n2 |
… |
nk |
Khi đó, công thức tính số trung bình trở thành
.
Trong đó n = n1 + n2 + … + nk. Ta gọi n là cỡ mẫu.
Chú ý: Nếu kí hiệu là tần số tương đối (hay còn gọi là tần suất) của xk trong mẫu số liệu thì số trung bình còn có thể biểu diễn là: .
6.2.Ý nghĩa của số trung bình
Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đo xu thế trung tâm của mẫu đó.
7. Trung vị và tứ phân vị
7.1. Trung vị
7.1.1 Định nghĩa và cách tính số trung vị
Khi các số liệu trong mẫu số liệu chênh lệch nhau quá lớn, ta dùng một đặc trưng khác của mẫu số liệu, gọi là trung vị để so sánh các mẫu số liệu với nhau.
Trung vị được định nghĩa như sau:
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
x1 ≤ x2 ≤ … ≤ xn.
Trung vị của mẫu, kí hiệu là Me, là giá trị ở chính giữa dãy x1, x2, …, xn. Cụ thể:
- Nếu n = 2k + 1, (tức n là số tự nhiên lẻ), thì trung vị của mẫu Me = xk + 1.
- Nếu n = 2k, (tức n là số tự nhiên chẵn), thì trung vị của mẫu Me = .
7.1.2 Ý nghĩa của số trung vị
Trung vị được dùng để đo xu thế trung tâm của mẫu số liệu. Trung vị là giá trị nằm ở chính giữa của mẫu số liệu theo nghĩa: luôn có ít nhất 50% số liệu trong mẫu lớn hơn hoặc bằng trung vị và ít nhất 50% số liệu trong mẫu nhỏ hơn hoặc bằng trung vị. Khi trong mẫu xuất hiện thêm một giá trị rất lớn hoặc rất nhỏ thì số trung bình sẽ bị thay đổi đáng kể nhưng trung vị thì ít thay đổi.
7.2. Tứ phân vị
• Trung vị chia mẫu thành hai phần. Trong thực tế người ta cũng quan tâm đến trung vị của mỗi phần đó. Ba trung vị này được gọi là tứ phân vị của mẫu.
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
x1 ≤ x2 ≤ … ≤ xn.
Tứ phân vị của một mẫu số liệu gồm ba giá trị, gọi là tứ phân vị thứ nhất, thứ hai và thứ ba (lần lượt kí hiệu là Q1, Q2, Q3). Ba giá trị này chia tập hợp dữ liệu đã sắp xếp thành bốn phần đều nhau. Cụ thể:
- Giá trị tứ phân vị thứ hai, Q2, chính là số trung vị của mẫu.
- Giá trị tứ phân vị thứ nhất, Q1, là trung vị của nửa số liệu đã sắp xếp bên trái Q2 (không bao gồm Q2 nếu n lẻ).
- Giá trị tứ phân vị thứ ba, Q3, là trung vị của nửa số liệu đã sắp xếp bên phải Q2 (không bao gồm Q2 nếu n lẻ).
• Ý nghĩa của tứ phân vị
Các điểm tứ phân vị Q1, Q2, Q3 chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần chia khoảng 25% tổng số liệu đã thu thập được.
Tứ phân vị thứ nhất Q1 còn được gọi là tứ phân vị dưới và đại diện cho nửa mẫu số liệu phía dưới. Tứ phân vị thứ ba Q3, còn được gọi là tứ phân vị trên và đại diện cho nửa mẫu số liệu ở phía trên.

8. Mốt
Cho mẫu số liệu dưới dạng bảng tần số. Giá trị có tần số lớn nhất được gọi là mốt của mẫu số liệu và kí hiệu là Mo.
Ý nghĩa của mốt: Mốt đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.
Chú ý: Một mẫu số liệu có thể có rất nhiều mốt. Khi tất cả các giá trị trong mẫu số liệu có tần số xuất hiện bằng nhau thì mẫu số liệu đó không có mốt.
9. Khoảng biến thiên và khoảng tứ phân vị
9.1. Khoảng biến thiên và khoảng tứ phân vị
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
x1 ≤ x2 ≤ … ≤ xn.
• Khoảng biến thiên của một mẫu số liệu, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó, tức là:
R = xn – x1.
• Khoảng tứ phân vị, kí hiệu là ∆Q, là hiệu giữa Q3 và Q1, tức là:
∆Q = Q3 – Q1.
9.2. Ý nghĩa của khoảng biến thiên và khoảng tứ phân vị
Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu.
Khoảng tứ phân vị đặc trưng cho độ phân tán của một nửa các số liệu, có giá trị thuộc đoạn từ Q1 đến Q3 trong mẫu.
Khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu.
9.3. Giá trị ngoại lệ
Khoảng tứ phân vị được dùng để xác định các giá trị ngoại lệ trong mẫu, đó là các giá trị quá nhỏ hay quá lớn so với đa số các giá trị của mẫu. Cụ thể, phần tử x trong mẫu là giá trị ngoại lệ nếu x > Q3 + 1,5∆Q hoặc x < Q1 – 1,5∆Q.
Sự xuất hiện của các giá trị ngoại lệ làm cho số trung bình và phạm vi của mẫu thay đổi lớn. Do đó, khi mẫu có giá trị ngoại lệ, người ta thường sử dụng trung vị và khoảng tứ phân vị để đo mức độ tập trung và mức độ phân tán của đa số các phần tử trong mẫu số liệu.
10. Phương sai và độ lệch chuẩn
10.1. Công thức tính phương sai và độ lệch chuẩn
* Giả sử ta có một mẫu số liệu là x1, x2, …, xn.
• Phương sai của mẫu số liệu này, kí hiệu là S2, được tính bởi công thức:
trong đó là số trung bình của mẫu số liệu.
• Căn bậc hai của phương sai được gọi là độ lệch chuẩn, kí hiệu là S.
Chú ý: Có thể biến đổi công thức tính phương sai ở trên thành:
.
Trong thống kê, người ta cũng quan tâm đến phương sai hiệu chỉnh, kí hiệu là , được tính bởi công thức:
.
* Giả sử mẫu số liệu được cho dưới dạng bảng tần số:
|
Giá trị |
x1 |
x2 |
… |
xk |
|
Tần số |
n1 |
n2 |
… |
nk |
Khi đó, công thức tính phương sai trở thành:
trong đó n = n1 + n2 + … + nk.
Có thể biến đổi công thức tính phương sai trên thành
.
10.2. Ý nghĩa của phương sai và độ lệch chuẩn
Phương sai là trung bình cộng của các bình phương độ lệch từ mỗi giá trị của mẫu số liệu đến số trung bình.
Phương sai và độ lệch chuẩn được dùng để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình. Phương sai và độ lệch chuẩn càng lớn thì các giá trị của mẫu càng cách xa nhau (có độ phân tán lớn).