Với giải Bài 56 trang 63 SBT Toán lớp 10 Cánh diều chi tiết trong Bài ôn tập chương 3 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải sách bài tập Toán lớp 10 Bài ôn tập chương 3

Bài 56 trang 63 SBT Toán 10 Tập 1: Hai địa điểm A và B cách nhau bởi một con sông (coi hai bờ sông song song). Người ta muốn xây một chiếc cầu bắc vuông góc với bờ sông để có thể đi từ A đến B. Với các số liệu (tính theo đơn vị ki – lô – mét) cho trên Hình 28, tìm x(km) để xác định vị trí đặt chân cầu sao cho khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A.

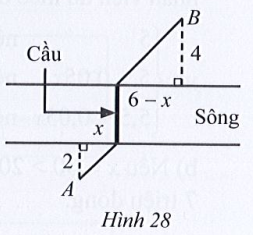
Lời giải

Đặt tọa độ các điểm như hình vẽ:

Ta có AD = x nên x > 0

Xét tam giác BHC vuông tại H, có:

BC² = BH² + CH² (định lí py – ta – go)

BC² = 4² + (6 – x)²

BC² = 16 + 36 – 12x + x²

BC² = x² – 12x + 52

BC = $\sqrt{x^2-12x+52}$

Xét tam giác AKD vuông tại K, có:

AD² = AK² + KD² (định lí py – ta – go)

AD² = 2² + x²

AD² = x² + 4

AD = $\sqrt{x^2+4}$

Để vị trí đặt chân cầu sao cho khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A ta có BC = 2AD

Hay $\sqrt{x^2-12x+52}=2\sqrt{x^2+4}$

Điều kiện x² + 4 ≥ 0 luôn đúng với mọi x.

⇔ x² – 12x + 52 = 4(x² + 4)

⇔ x² – 12x + 52 = 4x² + 16

⇔ 3x² + 12x –  36 = 0

⇔ x = 2 (thỏa mãn) hoặc x = – 6 (không thỏa mãn)

Vậy x = 2 thỏa mãn yêu cầu bài toán.

Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 45 trang 61 SBT Toán 10 Tập 1: Trong các hàm số sau, hàm số nào không là hàm số bậc hai?...

Bài 46 trang 61 SBT Toán 10 Tập 1: Tập nghiệm của bất phương trình – 5x² + 6x + 11 ≤ 0 là:...

Bài 47 trang 62 SBT Toán 10 Tập 1: Cho hàm số f(x) = $\left\{\begin{array}{l}1khix<0\\ 2khix>0\end{array}\right.$...

Bài 48 trang 62 SBT Toán 10 Tập 1: Cho hàm số y = f(x) có đồ thị ở Hình 24...

Bài 49 trang 62 SBT Toán 10 Tập 1: Một người vay 100 triệu đồng tại một ngân hàng để mua nhà với lãi suất r%/năm trong thời hạn 2 năm. Hỏi số tiền người này phải trả cho ngân hàng là bao nhiêu triệu đồng sau hai năm?...

Bài 50 trang 62 SBT Toán 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:...

Bài 51 trang 62 SBT Toán 10 Tập 1: Giải các bất phương trình bậc hai sau:...

Bài 52 trang 62 SBT Toán 10 Tập 1: Giải các phương trình sau:...

Bài 53 trang 62 SBT Toán 10 Tập 1: Hình 25 cho biết bảng giá cước của một hãng taxi (đã bao gồm thuế VAT):...

Bài 54 trang 63 SBT Toán 10 Tập 1: Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao h (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức h(x) = $\frac{1}{9000}{x}^2-\frac{7}{15}x+500$, trong đó x(feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo...

Bài 55 trang 63 SBT Toán 10 Tập 1: Bác Nam dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 6cm x 11cm, độ rộng viền xung quanh là x cm (Hình 27). Diện tích của viền khung ảnh không vượt quá 38 cm². Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu xăng – ti – mét?...

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Bài ôn tập chương 3

Bài 1: Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180°

Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 3: Khái niệm vectơ