Với giải sách bài tập Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Giải SBT Toán 10 trang 59 Tập 1

Bài 36 trang 59 SBT Toán 10 Tập 1: Trong các phát biểu sau, phát biểu nào đúng?

A. Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}$là tập nghiệm của phương trình f(x) = g(x).

B. Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}$là tập nghiệm của phương trình [f(x)]² = [g(x)]².

C. Mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình $\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}$

D. Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}$ là tập nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).

Lời giải

Đáp án đúng là D

Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}$ là tập nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).

Giải SBT Toán 10 trang 60 Tập 1

Bài 37 trang 60 SBT Toán 10 Tập 1: Trong các phát biểu sau, phát biểu nào đúng?

A. Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=g\left(x\right)$là tập nghiệm của phương trình f(x) = [g(x)]².

B. Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=g\left(x\right)$ là tập nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình g(x) ≥ 0.

C. Mọi nghiệm của phương trình f(x) = [g(x)]² đều là nghiệm của phương trình $\sqrt{f\left(x\right)}=g\left(x\right)$.

D. Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=g\left(x\right)$ là tập nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình f(x) ≥ 0.

Lời giải

Đáp án đúng là B.

Tập nghiệm của phương trình $\sqrt{f\left(x\right)}=g\left(x\right)$ là tập nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình g(x) ≥ 0.

Bài 38 trang 60 SBT Toán 10 Tập 1: Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = g(x) thỏa mãn một trong hai bất phương trình f(x) ≥ 0 hoặc g(x) ≥ 0 mà không cần kiểm tra thỏa mãn đồng thời cả hai bất phương trình đó để kết luận nghiệm của phương trình $\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}$.

Lời giải

Xét phương trình $\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}$ (*)

Điều kiện tồn tại căn thức là: f(x) ≥ 0 hoặc g(x) ≥ 0

Bình phương hai vế của phương trình (*) ta được: f(x) = g(x).

Do đó ta chỉ cần hoặc f(x) ≥ 0 hoặc g(x) ≥ 0 là đủ.

Bài 39 trang 60 SBT Toán 10 Tập 1: Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình g(x) ≥ 0 mà không cần kiểm tra thỏa mãn bất phương trình f(x) ≥ 0 để kết luận nghiệm của phương trình $\sqrt{f\left(x\right)}=g\left(x\right)$.

Lời giải

Xét $\sqrt{f\left(x\right)}=g\left(x\right)$ (**)

Điều kiện của phương trình gồm:

+) Điều kiện tồn tại của căn thức là f(x) ≥ 0

+) Vì $\sqrt{f\left(x\right)}$ ≥ 0 nên g(x) ≥ 0.

Bình phương 2 vế của phương trình (**) là: f(x) = [g(x)]² ≥ 0

Do đó trong hai điều kiện ta chỉ cần g(x) ≥ 0.

Bài 40 trang 60 SBT Toán 10 Tập 1: Giải các phương trình sau:

a) $\sqrt{-4x+4}=\sqrt{-x^2+1}$;

b) $\sqrt{3x^2-6x+1}=\sqrt{x^2-3}$;

c) $\sqrt{2x-1}=3x-4$;

d) $\sqrt{-2x^2+x+7}=x-3$.

Lời giải

a) $\sqrt{-4x+4}=\sqrt{-x^2+1}$ (1)

Điều kiện – 4x + 4 ≥ 0 ⇔ x ≤ 1

(1) ⇔ – 4x + 4 = – x² + 1

⇔ x² – 4x + 3 = 0

⇔ x = 3 (không thỏa mãn) và x = 1 (thỏa mãn)

Vậy nghiệm của phương trình là x = 1.

b) $\sqrt{3x^2-6x+1}=\sqrt{x^2-3}$

Điều kiện x² – 3 ≥ 0 ⇔ $\left[\begin{array}{l}x\le -\sqrt{3}\\ x\ge \sqrt{3}\end{array}\right.$

(1) ⇔ 3x² – 6x + 1 = x² – 3

⇔ 2x² – 6x + 4 = 0

⇔ x = 2 (thỏa mãn) và x = 1 (không thỏa mãn)

Vậy nghiệm của phương trình là x = 2.

c) $\sqrt{2x-1}=3x-4$

Điều kiện 3x – 4 ≥ 0 ⇔ x  ≥ $\frac{4}{3}$ 

(1) ⇔ 2x – 1 = 9x² – 24x + 16

⇔ 9x² – 26x + 17 = 0

⇔ x = 1 (không thỏa mãn) và x = $\frac{17}{9}$(thỏa mãn)

Vậy nghiệm của phương trình là x = $\frac{17}{9}$.

d) $\sqrt{-2x^2+x+7}=x-3$

Điều kiện x – 3 ≥ 0 ⇔ x  ≥ 3

(1) ⇔ – 2x² + x + 7 = x – 3

⇔ – 2x² + 10 = 0

⇔ x² = 5

⇔ x = $\sqrt{5}$(không thỏa mãn) và x = $-\sqrt{5}$(không thỏa mãn)

Vậy nghiệm của phương trình là x ∈ $\varnothing$.

Bài 41 trang 60 SBT Toán 10 Tập 1: Giải các phương trình sau:

a) $\sqrt{7-2x}+x=2$;

b) $\sqrt{-2x^2+7x+1}+3x=7$.

Lời giải

a) $\sqrt{7-2x}+x=2$

⇔ $\sqrt{7-2x}=2-x$

Điều kiện 2 – x ≥ 0 ⇔ x ≤ 2

⇔ 7 – 2x = 4 – 4x + x²

⇔ x² – 2x – 3 = 0

⇔ x = – 1 (thỏa mãn) hoặc x = 3 (không thỏa mãn)

Vậy phương trình đã cho có nghiệm x = – 1.

b) $\sqrt{-2x^2+7x+1}+3x=7$.

⇔ $\sqrt{-2x^2+7x+1}=7-3x$

Điều kiện 7 – 3x ≥  0 ⇔ x ≤ $\frac{7}{3}$

⇔ – 2x² + 7x + 1 = 49 – 42x + 9x²

⇔ 11x² – 49x + 48 = 0

⇔ x = 3 (không thỏa mãn) hoặc x = $\frac{16}{11}$ (thỏa mãn)

Vậy phương trình đã cho có nghiệm x = $\frac{16}{11}$.

Bài 42 trang 60 SBT Toán 10 Tập 1: Để leo lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m. Ban đầu bác Dũng đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên của bức tường (Hình 21a). Sau đó, bác Dũng dịch chuyển chân thang vào gần bức tường thêm 1m thì bác Dũng nhận thấy thang tạo với mặt đất một góc 45° (Hình 21b). Bức tường cao bao nhiêu mét?

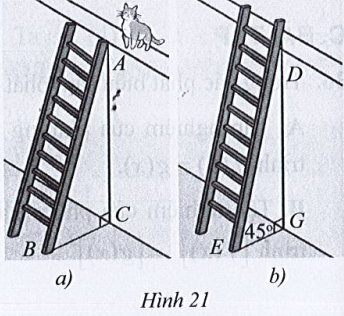
Lời giải

+) Hình 21a):

Đặt AC = x (m). Khi đó AB = x + 2

Xét tam giác ABC vuông tại C, có AC = x, AB = x + 2

Áp dụng định lí py – ta – go ta được:

AB² = AC² + BC²

⇔ (x + 2)² = x² + BC²

⇔ BC² = (x  + 2)² – x²

⇔ BC² = 4x + 4

⇔ BC = $\sqrt{4x+4}$

AC là chiều cao của bức tường nên AC = DG = x.

⇒ DG = BC – 1 = $\sqrt{4x+4}$ - 1

Xét tam giác DGE vuông tại G, có:

tanE = $\frac{DG}{GE}$

⇔ tan45°  $=\frac{x}{\sqrt{4x+4}-1}$

⇔ 1  $=\frac{x}{\sqrt{4x+4}-1}$

⇔ $\sqrt{4x+4}$ – 1 = x

⇔ $\sqrt{4x+4}$ = x + 1 (điều kiện x ≥ – 1)

⇔ x² + 2x + 1 = 4x + 4

⇔ x² – 2x – 3 = 0

⇔ x = 3 (thỏa mãn) và x = – 1 (không thỏa mãn)

Vậy bức tường cao 3 m.

Giải SBT Toán 10 trang 61 Tập 1

Bài 43 trang 61 SBT Toán 10 Tập 1: Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300m và gặp người đi bộ tại địa điểm cách B một khoảng BH = 1 400m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).

a) Tính khoảng cách CB.

b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc.

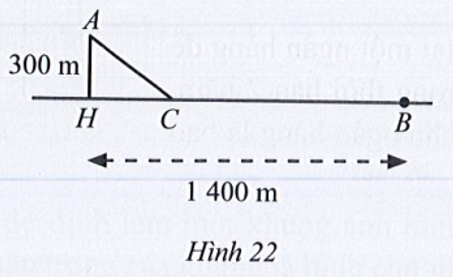
Lời giải

a) Đặt CH = x (x ≥ 0). Khi đó BC = 1 400 – x.

Xét tam giác AHC vuông tại H, có:

AH² + HC² = AC²

⇔ AC² = 300² + x²

⇔ AC = $\sqrt{x^2+90000}$

Thời gian thuyền đi từ A đến C là: $\frac{\sqrt{x^2+90000}}{3}$ (giờ)

Thời gian người đi bộ đi từ B đến C là $\frac{1400-x}{6}$ (giờ)

Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C nên ta có:

$\frac{\sqrt{x^2+90000}}{3}=\frac{1400-x}{6}$

⇔ $2\sqrt{x^2+90000}=1400-x$ (điều kiện x ≤ 1 400)

⇔ 4(x² + 90 000) = 1 960 000 – 2 800x + x²

⇔ 3x² + 2 800x – 1 600 000 = 0

⇔ x = 400 (TMĐK) hoặc x = $-\frac{4000}{3}$ (không TMĐK)

⇒ CB = 1 400 – x = 1 400 – 400 = 1 000 (m).

Vậy khoảng cách CB = 1 000 m.

b) Đổi 1 000 m = 1km.

Thời gian hai nguời xuất phát cho tới khi gặp nhau là: $\frac{1}{6}$(giờ)

Vậy từ khi xuất phát hai người mất $\frac{1}{6}$ giờ cho đến khi gặp nhau.

Bài 44 trang 61 SBT Toán 10 Tập 1: Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140 m.

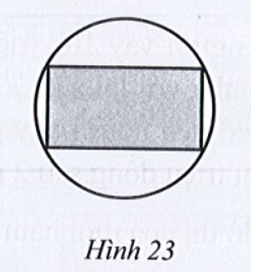
Lời giải

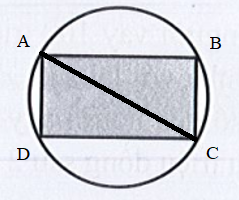
Đặt tọa độ các đỉnh của hình chữ nhật là ABCD.

Vì ABCD nội tiếp hình tròn nên AC là đường kính. Do đó AC = 50 m.

Gọi chiều dài của hình chữ nhật là x (m) (x > 0).

Khi đó AB = DC = x(m)

Xét tam giác ABC vuông tại B, có:

AC² = AB² + BC² (định lý py – ta – go)

⇔ 50² = x² + BC²

⇔ BC² = 2 500 – x²

⇔ BC = $\sqrt{2500-x^2}$

Tổng quãng đường đi xung quanh vườn chính là chu vi hình chữ nhật và bằng 140m, nên ta có: 2(x + $\sqrt{2500-x^2}$) = 140

⇔ $\sqrt{2500-x^2}$ = 70 – x (điều kiện x ≤ 70)

⇔ 2 500 – x² = 4 900 – 140x + x²

⇔ 2x² – 140x  + 2 400 = 0

⇔ x = 40 (TM) hoặc x = 30 (TM)

Nếu một cạnh bằng 40m thì cạnh còn lại là 30m, nếu một cạnh bằng 30m thì cạnh còn lại là 40m.

Vậy kích thước của hình chữ nhật là 40m và 30m.