Với lời giải SBT Toán 10 trang 56 Tập 1 chi tiết trong Bài 2: Hàm số bậc hai sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 2: Hàm số bậc hai
Bài 7 trang 56 SBT Toán 10 Tập 1: Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu Nhật Tân là
y = f(x) = (đơn vị đo: mét).
a) Hãy tính chiều dài đoạn dây dọi sử dụng nếu khoảng cách từ chân của trụ cầu đến quả nặng là 30 cm.
b) Hãy tính khoảng cách từ chân trụ cầu đến quả nặng nếu biết chiều dài đoạn dây dọi sử dụng là 15 m.
Lời giải:
Từ Bài 4 phần Bài tập mẫu, ta có đồ thị hàm số y = f(x) = như hình sau:
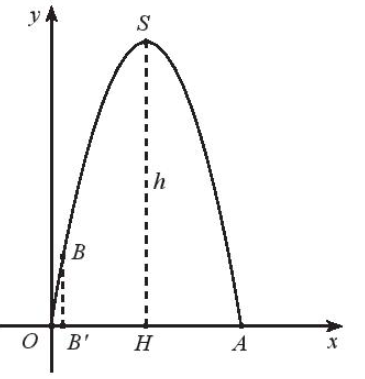
Ta xét điểm B trên hình.
a) Đổi 30 cm = 0,3 m.
Chiều dài l của đoạn dây dọi sử dụng là tung độ của điểm B trên parabol có xB = 0,3.
Nên ta có: l = BB’ = f(0,3) = (m).
Vậy chiều dài dây dọi khoảng 2,8 m.
b) Khoảng cách từ chân trụ đến quả nặng là hoành độ điểm B trên parabol với yB = 15.
Ta có: = 15.
⇔ – 187xB2 + 8041xB – 12840 = 0
Suy ra x1 ≈ 41,34 và x2 ≈ 1,66.
Vậy khoảng cách từ chân trụ cầu bên trái đến quả nặng là khoảng 1,66 m, khoảng cách từ chân trụ cầu bên phải đến quả nặng là khoảng 41,34 m.
Theo đề bài, ta chọn kết quả 1,66 m.
Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Giải SBT Toán 10 trang 54 Tập 1
Giải SBT Toán 10 trang 55 Tập 1
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của một góc từ 0 đến 180
Bài 2: Định lí côsin và định lí sin
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
