Giải SBT Toán 10 trang 50 Tập 2 Kết nối tri thức

Nguyễn Mạnh Tài Ngày: 21-11-2022 Lớp 10

415

Với lời giải SBT Toán 10 trang 50 Tập 2 chi tiết trong Bài tập cuối chương 7 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 7

Bài 7.56 trang 50 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai điểm A(–1; 0) và B(3; 1).

a) Viết phương trình đường tròn tâm A và đi qua B.

b) Viết phương trình tổng quát của đường thẳng AB.

c) Viết phương trình đường tròn tâm O và tiếp xúc với đường thẳng AB.

Lời giải:

Đường tròn tâm A đi qua B có bán kính R = AB = $\sqrt{{(3 + 1)}^{2} + {(1 - 0)}^{2}} = \sqrt{17}$ .

Vậy phương trình đường tròn tâm A đi qua B là:

(x + 1)² + (y – 0)² = ( )²

⇔ (x + 1)² + y² = 17.

Ta có $\vec{A B} = (4; 1)$ là một vectơ chỉ phương của đường thẳng AB. Do đó $\vec{n} = (- 1; 4)$ là một vectơ pháp tuyến của AB.

Phương trình đường thẳng AB là:

–1(x + 1) + 4(y – 0) = 0

⇔ –x – 1 + 4y = 0

⇔ x – 4y + 1 = 0.

Đường tròn tâm O và tiếp xúc với đường thẳng AB có bán kính là

$R = d (O, A B) = \frac{|0 - 4.0 + 1|}{\sqrt{1^{2} + {(- 4)}^{2}}} = \frac{1}{\sqrt{17}}$

Vậy phương trình đường tròn tâm O tiếp xúc với AB là

${(x - 0)}^{2} + {(y - 0)}^{2} = {(\frac{1}{\sqrt{17}})}^{2} \Leftrightarrow x^{2} + y^{2} = \frac{1}{17}$ .

Bài 7.57 trang 50 SBT Toán 10 Tập 2: Cho đường tròn (C) có phương trình x² + y² – 4x + 6y – 12 = 0.

a) Tìm toạ độ tâm I và bán kính R của (C).

b) Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.

Lời giải:

Xét phương trình đường tròn (C) , ta có:

I (a; b) với a = – 4 : (–2) = 2, b = 6 : (–2) = –3, do đó, I (2; –3)

$R = \sqrt{2^{2} + {(- 3)}^{2} - (- 12)} = 5$ .

Thay toạ độ điểm M vào phương trình của đường tròn (C) ta có

5² + 1² – 4.5 + 6.1 – 12 = 0 (luôn đúng)

nên điểm M thuộc đường tròn (C).

Tiếp tuyến d của (C) tại điểm M là đường thẳng đi qua M và vuông góc với IM nên có một vectơ pháp tuyến là $\vec{I M} = (3; 4)$ .

Vậy phương trình của tiếp tuyến d là:

3(x – 5) + 4(y – 1) = 0

⇔ 3x + 4y – 19 = 0.

Bài 7.58 trang 50 SBT Toán 10 Tập 2: Các phương trình dưới đây là phương trình chính tắc của đường nào? Khi đó hãy tìm các tiêu điểm, tiêu cự, đường chuẩn (nếu là đường parabol).

a) y²= 10x.

b) x² – y² = 1.

c) $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ .

Lời giải:

y² = 10x là phương trình chính tắc của parabol.

Ta có y² = 10x = 2px ⇒ p = 5 $\Rightarrow \frac{p}{2} = \frac{5}{2}$ .

Parabol trên có tiêu điểm là $F (\frac{5}{2}; 0)$ , phương trình đường chuẩn là $x + \frac{5}{2} = 0$ .

x² – y² = 1 là phương trình chính tắc của hypebol với a = b = 1 nên $c = \sqrt{a^{2} + b^{2}} = \sqrt{2}$

Tiêu điểm là $F_{1} (- \sqrt{2}; 0), F_{2} (\sqrt{2}; 0)$ tiêu cự là $2 c = 2 \sqrt{2}$ .

$\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ là phương trình chính tắc của elip với a² = 25, b² = 16, $c = \sqrt{a^{2} - b^{2}} = 3$

Tiêu điểm là F₁(–3; 0), F₂(3; 0), tiêu cự F₁F₂ = 2c = 2.3 = 6.

Bài 7.59 trang 50 SBT Toán 10 Tập 2: Cho elip (E) có phương trình là $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ . Tìm toạ độ các điểm M thuộc (E), biết rằng M nhìn hai tiêu điểm của (E) dưới một góc vuông.

Lời giải:

Elip $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ có a² = 25, b² = 9, c = $\sqrt{a^{2} - b^{2}} = \sqrt{25 - 9} = 4$ nên hai tiêu điểm là F₁(–4; 0), F₂(4; 0).

Do M nhìn hai tiêu điểm dưới một góc vuông nên M nằm trên đường tròn (C) tâm O đường kính F₁F₂ = 2.4 = 8 nên bán kính là R = 4.

Phương trình đường tròn (C) là:

x² + y² = 4² hay x² + y² = 16.

Khi đó toạ độ của M là nghiệm của hệ phương trình

$\{\begin{matrix} x^{2} + y^{2} = 16 \\ \frac{x^{2}}{25} + \frac{y^{2}}{9} = 1 \end{matrix} \Leftrightarrow \{\begin{matrix} y^{2} = 16 - x^{2} \\ \frac{x^{2}}{25} + \frac{16 - x^{2}}{9} = 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} y^{2} = 16 - x^{2} \\ 9 x^{2} + 400 - 25 x^{2} = 225 \end{matrix} \Leftrightarrow \{\begin{matrix} y^{2} = 16 - x^{2} \\ 16 x^{2} = 175 \end{matrix} \Leftrightarrow \{\begin{matrix} y^{2} = 16 - \frac{175}{16} \\ x^{2} = \frac{175}{16} \end{matrix}$

$\Leftrightarrow \{\begin{cases} x = \pm \frac{5 \sqrt{7}}{4} \\ y = \pm \frac{9}{4} \end{cases}$ .

Vậy ta tìm được bốn điểm M thoả mãn là $M (\pm \frac{5 \sqrt{7}}{4}; \pm \frac{9}{4})$ .

Bài 7.60 trang 50 SBT Toán 10 Tập 2: Lập phương trình chính tắc của parabol (P) biết rằng, (P) đi qua điểm A(2; 4). Khi đó hãy tìm điểm M thuộc (P) và cách tiêu điểm của (P) một khoảng bằng 5.

Lời giải:

Phương trình chính tắc của (P) có dạng y²= 2px.

Do (P) đi qua điểm A(2; 4) nên ta có: 4² = 2p.2 ⇔ p = 4 .

Vậy phương trình chính tắc của (P) là: y² = 8x với tiêu điểm F(2; 0).

Ta còn viết phương trình (P) dưới dạng: $x = \frac{y^{2}}{8}$ .

Ta có:

Do điểm M thuộc (P) nên toạ độ của điểm M có dạng $M (\frac{t^{2}}{8}; t)$

Từ giả thiết MF = 5 ta suy ra:

MF² = 25

$\begin{array}{l} \Leftrightarrow {(\frac{t^{2}}{8} - 2)}^{2} + t^{2} = 25 \\ \Leftrightarrow \frac{t^{4}}{64} - \frac{t^{2}}{2} + 4 + t^{2} = 25 \\ \Leftrightarrow \frac{t^{4}}{64} + \frac{t^{2}}{2} - 21 = 0 (*) \end{array}$

Đặt t² = X (X ≥ 0) ta có:

(*) ⇔ $\frac{X^{2}}{64} + \frac{X}{2} - 21 = 0 \Leftrightarrow [\begin{array}{l} X = 24 (T M) \\ X = - 56 (L) \end{array}$

Với X = 24 ⇔ $t = \pm 2 \sqrt{6}$

Vậy có hai điểm M thoả mãn là $M (3; \pm 2 \sqrt{6})$ .

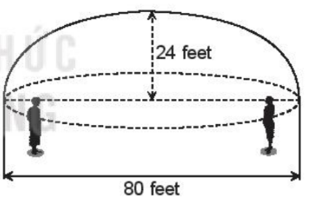
Bài 7.61 trang 50 SBT Toán 10 Tập 2: Hình vẽ bên minh hoạ một phòng thì thầm (whispering gallery) với mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet. Một âm thanh được phát ra từ một tiêu điểm của phòng thì thầm có thể được nghe thấy tại tiêu điểm còn lại. Hỏi hai người nói thầm qua lại với nhau thì sẽ cách trung tâm của phòng bao nhiêu mét ? Theo đơn vị đo lường quốc tế, 1 feet = 0,3048 m.

Sách bài tập Toán 10 Bài tập cuối chương 7 - Kết nối tri thức (ảnh 1)

Lời giải:

Theo đề bài, mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet nên mặt cắt của phòng thì thầm là một nửa elip có a = 40 feet, b = 24 feet nên $c = \sqrt{a^{2} - b^{2}} = \sqrt{40^{2} - 24^{2}} = 32$ feet