Với giải bài 57 trang 92 Toán lớp 8 chi tiết trong Ôn tập chương 3 Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Ôn tập chương 3 Hình học

Bài 57 trang 92 Toán 8 Tập 2: Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.

Lời giải:

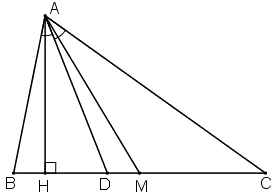
D luôn nằm giữa H và M.

- Ta chứng minh: D luôn nằm giữa H và M.

Vì AD là đường phân giác của tam giác ABC nên:

$\frac{AB}{AC}=\frac{DB}{DC}$

Mà AB < AC nên DB < DC

Suy ra: DB + DC <  DC + DC

Hay BC < 2DC

Suy ra: $DC>\frac{BC}{2}$

Mà M là trung điểm của BC nên

 $MC=\frac{BC}{2}$

Suy ra: DC > MC nên M nằm giữa D và C   (1).

Vì tam giác CAH vuông tại H nên:

 $\widehat{CA\text{}H}={90}^0-\widehat{C}$

Tổng ba góc của 1 tam giác bằng 180⁰ nên:

$$\begin{gathered} \widehat{A}+\widehat{B}+\widehat{C}={180}^0 \\ \Rightarrow {90}^0=\frac{1}{2}.\left(\widehat{A}+\widehat{B}+\widehat{C}\right) \end{gathered}$$

Suy ra:

$$\begin{gathered} \widehat{CAH}=\frac{1}{2}\left(\widehat{A}+\widehat{B}+\widehat{C}\right)-\widehat{C} \\ =\frac{1}{2}\left(\widehat{A}+\widehat{B}-\widehat{C}\right) \end{gathered}$$

Vì AB < AC nên 

$\widehat{C}<\widehat{\text{}B}\Rightarrow \widehat{B}-\widehat{C}>0^0$

(trong 1 tam giác đối diện với cạnh lớn hơn thì góc đó lớn hơn).

Do đó: $\widehat{CAH}>\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{2}\widehat{A}\iff \widehat{CAH}>\widehat{CAD}$

Suy ra: tia AD nằm giữa hai tia AH và AC.

Suy ra: D nằm giữa H và C    (2).

Từ (1) và (2) suy ra: D nằm giữa H và M.

Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

Câu hỏi 1 trang 89 Toán 8 Tập 2: Phát biểu và viết tỉ lệ thức biểu thị hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thằng A'B' và C'D'...

Câu hỏi 2 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - let trong tam giác...

Câu hỏi 3 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - let đảo...

Câu hỏi 4 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Ta - let...

Câu hỏi 5 trang 89 Toán 8 Tập 2: Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận)...

Câu hỏi 6 trang 89 Toán 8 Tập 2: Phát biểu định nghĩa hai tam giác đồng dạng...

Câu hỏi 7 trang 89 Toán 8 Tập 2: Phát biểu định lí về đường thẳng song song với một cạnh của tam giác và cắt hai cạnh (hoặc phần kéo dài của hai cạnh) còn lại...

Câu hỏi 8 trang 89 Toán 8 Tập 2: Phát biểu định lí về ba trường hợp đồng dạng của hai tam giác...

Câu hỏi 9 trang 89 Toán 8 Tập 2: Phát biểu định lí về trường hợp đồng dạng đặc biệt của hai tam giác vuông (trường hợp cạnh huyền và một cạnh góc vuông)...

Bài 56 trang 92 Toán 8 Tập 2: Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau:...

Bài 58 trang 92 Toán 8 Tập 2: Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h.66)...

Bài 59 trang 92 Toán 8 Tập 2: Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD...

Bài 60 trang 92 Toán 8 Tập 2: Cho tam giác vuông ABC, $\widehat{A}$= 90^o, $\widehat{C}$ = 30^o và đường phân giác BD (D thuộc cạnh AC)...

Bài 61 trang 92 Toán 8 Tập 2: Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường chéo BD = 10cm...