Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Ôn tập chương 3 Hình học hay, chi tiết giúp học sinh dễ dàng làm bài tập Ôn tập chương 3 Hình học lớp 8.

Giải bài tập Toán lớp 8 Ôn tập chương 3 Hình học

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 89 Toán 8 Tập 2: Phát biểu và viết tỉ lệ thức biểu thị hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thằng A'B' và C'D'.

Trả lời:

Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức:

$\frac{AB}{CD}=\frac{A\text{'}B\text{'}}{C\text{'}D}$ hoặc $\frac{AB}{A\text{'}B\text{'}}=\frac{CD}{C\text{'}D\text{'}}$

Câu hỏi 2 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - let trong tam giác.

Trả lời:

Định lí Talet trong tam giác:

Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

Câu hỏi 3 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - let đảo.

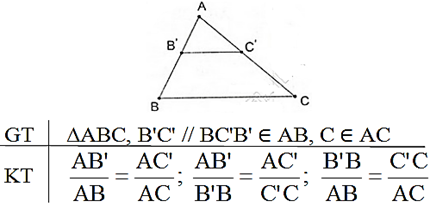
Trả lời:

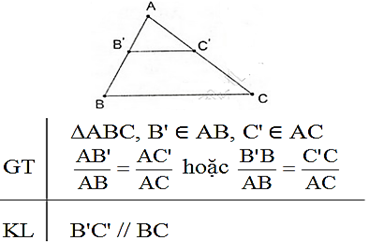
Định lí Talet đảo:

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Câu hỏi 4 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Ta - let.

Trả lời:

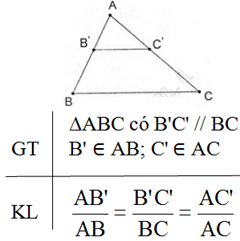
Hệ quả của định lí Talet:

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.

Câu hỏi 5 trang 89 Toán 8 Tập 2: Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận).

Trả lời:

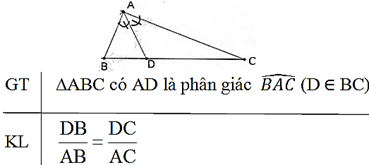
Định lý:

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.

Câu hỏi 6 trang 89 Toán 8 Tập 2: Phát biểu định nghĩa hai tam giác đồng dạng.

Trả lời:

Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:

$\begin{array}{l}\widehat{A\text{'}}=\widehat{A};\widehat{B\text{'}}=\widehat{B};\widehat{C\text{'}}=\widehat{C}\\ \frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}C\text{'}}{BC}=\frac{C\text{'}A\text{'}}{CA}\end{array}$

Câu hỏi 7 trang 89 Toán 8 Tập 2: Phát biểu định lí về đường thẳng song song với một cạnh của tam giác và cắt hai cạnh (hoặc phần kéo dài của hai cạnh) còn lại.

Trả lời:

Định lí:

Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Câu hỏi 8 trang 89 Toán 8 Tập 2: Phát biểu định lí về ba trường hợp đồng dạng của hai tam giác.

Trả lời:

- Trường hợp 1 (c.c.c):

Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

- Trường hợp 2 (c.g.c):

Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.

- Trường hợp 3 (g.g):

Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

Câu hỏi 9 trang 89 Toán 8 Tập 2: Phát biểu định lí về trường hợp đồng dạng đặc biệt của hai tam giác vuông (trường hợp cạnh huyền và một cạnh góc vuông).

Trả lời:

Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

Bài tập (trang 92)

Bài 56 trang 92 Toán 8 Tập 2: Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau:

a) AB = 5cm, CD = 15cm;

b) AB = 45dm; CD = 150cm;

c) AB = 5CD.

Lời giải:

a) $\frac{AB}{CD}=\frac{5}{15}=\frac{1}{3}$.

b) Đổi 45dm = 450 cm

Ta có: $\frac{AB}{CD}=\frac{450}{150}=3$.

c) Vì AB = 5CD nên $\frac{AB}{CD}=\frac{5CD}{CD}=5$.

Bài 57 trang 92 Toán 8 Tập 2: Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.

Lời giải:

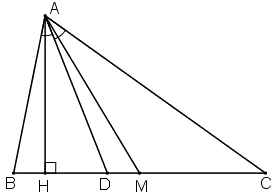
D luôn nằm giữa H và M.

- Ta chứng minh: D luôn nằm giữa H và M.

Vì AD là đường phân giác của tam giác ABC nên:

$\frac{AB}{AC}=\frac{DB}{DC}$

Mà AB < AC nên DB < DC

Suy ra: DB + DC <  DC + DC

Hay BC < 2DC

Suy ra: $DC>\frac{BC}{2}$

Mà M là trung điểm của BC nên

 $MC=\frac{BC}{2}$

Suy ra: DC > MC nên M nằm giữa D và C   (1).

Vì tam giác CAH vuông tại H nên:

 $\widehat{CA\text{}H}={90}^0-\widehat{C}$

Tổng ba góc của 1 tam giác bằng 180⁰ nên:

$$\begin{gathered} \widehat{A}+\widehat{B}+\widehat{C}={180}^0 \\ \Rightarrow {90}^0=\frac{1}{2}.\left(\widehat{A}+\widehat{B}+\widehat{C}\right) \end{gathered}$$

Suy ra:

$$\begin{gathered} \widehat{CAH}=\frac{1}{2}\left(\widehat{A}+\widehat{B}+\widehat{C}\right)-\widehat{C} \\ =\frac{1}{2}\left(\widehat{A}+\widehat{B}-\widehat{C}\right) \end{gathered}$$

Vì AB < AC nên 

$\widehat{C}<\widehat{\text{}B}\Rightarrow \widehat{B}-\widehat{C}>0^0$

(trong 1 tam giác đối diện với cạnh lớn hơn thì góc đó lớn hơn).

Do đó: $\widehat{CAH}>\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{2}\widehat{A}\iff \widehat{CAH}>\widehat{CAD}$

Suy ra: tia AD nằm giữa hai tia AH và AC.

Suy ra: D nằm giữa H và C    (2).

Từ (1) và (2) suy ra: D nằm giữa H và M.

Bài 58 trang 92 Toán 8 Tập 2: Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h.66).

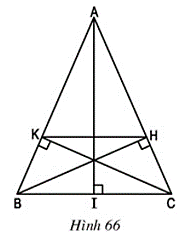
a) Chứng minh BK = CH.

b) Chứng minh KH // BC.

c) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.

Hướng dẫn câu c):

- Vẽ thêm đường cao AI, xét hai tam giác đồng dạng IAC và HBC rồi tính CH.

- Tiếp theo, xét hai tam giác đồng dạng AKH và ABC rồi tính HK.

Lời giải:

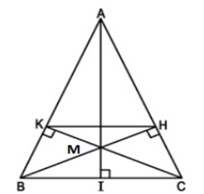
a) Xét tam giác BKC và tam giác CHB có:

BC chung

$\widehat{ABC}=\widehat{ACB}$(vì tam giác ABC cân tại A)

$\widehat{BKC}=\widehat{BHC}={90}^0$

Do đó, ∆BKC = ∆CHB (cạnh huyền – góc nhọn).

Suy ra: BK = CH.

b) Ta có: Tam giác ABC cân tại A nên AB = AC

Theo ý a ta có BK = CH

Suy ra: AK = AH (do AB = AC tam giác cân)

Do đó: $\frac{AK}{AB}=\frac{AH}{AC}$

Suy ra: KH // BC (định lí Ta- let đảo).

c) Ta có: đường cao BH cắt đường cao CK tại M nên M là trực tâm tam giác ABC

Suy ra: AM vuông góc BC tại I.

Ta có: ∆AIC $~$ ∆ BHC ( vì $\widehat{AIC}=\widehat{BHC}={90}^0;\widehat{C}chung)$

$$\begin{gathered} \Rightarrow \frac{IC}{HC}=\frac{AC}{BC} \\ \Rightarrow \frac{\frac{a}{2}}{HC}=\frac{b}{a} \\ \Rightarrow HC=\frac{a^2}{2b} \\ \Rightarrow AH=AC-HC \\ =b-\frac{a^2}{2b} \\ =\frac{2b^2-a^2}{2b} \end{gathered}$$

Mà HK // BC nên

$$\begin{gathered} \frac{HK}{BC}=\frac{AH}{AC} \\ \Rightarrow HK=\frac{BC.AH}{AC} \end{gathered}$$

Suy ra:

$$\begin{gathered} HK=\frac{a}{b}.\left(\frac{2b^2-a^2}{2b}\right) \\ =\frac{2a{b}^2-a^3}{2b^2} \end{gathered}$$

Bài 59 trang 92 Toán 8 Tập 2: Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.

Lời giải:

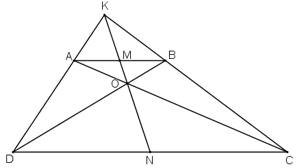
Gọi KO cắt AB, CD lần lượt tại M, N.

Xét ΔKDN có AM // DN (A ∈ KD, M ∈ KN)

⇒ $\frac{AM}{DN}=\frac{KM}{KN}$  (Hệ quả định lý Ta - let)  (1)

Xét ΔKCN có BM // CN (M ∈ KN, B ∈ KC)

⇒  $\frac{MB}{NC}=\frac{KM}{KN}$  (Hệ quả định lý Ta - let)  (2)

Từ (1); (2) suy ra:

 $$\begin{gathered} \frac{AM}{DN}=\frac{MB}{NC} \\ \Rightarrow \frac{AM}{BM}=\frac{DN}{CN}\left(3\right) \end{gathered}$$

Xét ΔOCN có AM // NC (A ∈ OC, M ∈ ON)

⇒  $\frac{AM}{CN}=\frac{OM}{ON}$ (Hệ quả định lý Ta - let)

Xét ΔODN có MB // ND (M ∈ ON, B ∈ OD)

⇒ $\frac{MB}{ND}=\frac{OM}{ON}$  (Hệ quả định lý Ta - let)

Suy ra:

 $$\begin{gathered} \frac{AM}{CN}=\frac{BM}{ND} \\ \Rightarrow \frac{AM}{BM}=\frac{CN}{DN}\left(\text{}4\right) \end{gathered}$$

Từ (3) và (4) suy ra

$\frac{DN}{CN}=\frac{CN}{DN}$

⇒ CN = DN

⇒ AM = MB

Vậy M, N là trung điểm AB, CD.

Bài 60 trang 92 Toán 8 Tập 2: Cho tam giác vuông ABC, $\widehat{A}$= 90^o, $\widehat{C}$ = 30^o và đường phân giác BD (D thuộc cạnh AC).

a) Tính tỉ số $\frac{AD}{CD}$.

b) Cho biết độ dài AB = 12,5cm. Hãy tính chu vi và diện tích của tam giác ABC.

Lời giải:

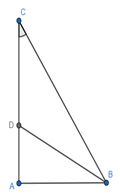
a)

+ Xét Δ ABC vuông tại A, có $\widehat{C}={30}^0$

$\Rightarrow AB=\frac{1}{2}BC$

(Trong một tam giác vuông, cạnh đối diện với góc 30^o bằng một nửa cạnh huyền)

+ Xét ΔABC có BD là phân giác của $\widehat{B}$

$\Rightarrow \frac{AD}{DC}=\frac{AB}{BC}$(tính chất đường phân giác) 

Mà $AB=\frac{1}{2}BC$ nên $\frac{AB}{BC}=\frac{1}{2}$.

Suy ra: $\frac{AD}{DC}=\frac{1}{2}$.

b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm

Áp dụng định lí Py- ta- go vào tam giác ABC ta có:

AB² + AC² = BC² nên AC² = BC² - AB²

$$\begin{gathered} \Rightarrow AC=\sqrt{B{C}^2-A{B}^2} \\ =\sqrt{{25}^2-12,5^2} \\ =12,5\sqrt{3}\approx 21,65cm \end{gathered}$$

+ Chu vi tam giác ABC là:

P = AB + BC + CA

 $$\begin{gathered} =12,5+\text{\hspace{0.17em}}25+12,5.\sqrt{3} \\ =37,5+\text{\hspace{0.17em}\hspace{0.17em}}12,5.\sqrt{3} \end{gathered}$$

+ Diện tích tam giác ABC là:

$$\begin{gathered} S=\frac{1}{2}.AB.AC \\ =\frac{1}{2}.12,5.12,5.\sqrt{3} \\ \approx 135,32c{m}^2 \end{gathered}$$

Bài 61 trang 92 Toán 8 Tập 2: Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường chéo BD = 10cm.

a) Nêu cách vẽ tứ giác ABCD có kích thước đã cho ở trên.

b) Các tam giác ABD và BDC có đồng dạng với nhau không? Vì sao?

c) Chứng minh rằng AB // CD.

Lời giải:

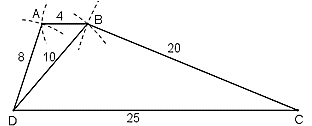
a) Cách vẽ:

- Vẽ ΔBDC:

+ Vẽ DC = 25cm

+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.

Nối DB và BC.

- Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.

Nối DA và BA.

Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.

b) Ta có:

$\begin{array}{l}\frac{AB}{BD}=\frac{4}{10}=\frac{2}{5};\\ \frac{BD}{DC}=\frac{10}{25}=\frac{2}{5}\text{;}\\ \frac{AD}{BC}=\frac{8}{20}=\frac{2}{5}\\ \Rightarrow \frac{AB}{BD}=\frac{BD}{DC}=\frac{AD}{BC}\end{array}$

Suy ra:  ∆ABD $~$ ∆BDC  (c.c.c)

c) Vì ∆ABD $~$ ∆BDC nên $\widehat{ABD}=\widehat{BDC}$ (hai góc tương ứng)

Mà 2 góc này ở vị trí so le trong nên AB // DC

Dó đó: ABCD là hình thang.