Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu hay, chi tiết giúp học sinh dễ dàng làm bài tập Hình cầu. Diện tích mặt cầu và thể tích hình cầu lớp 9.

Giải bài tập Toán lớp 9 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 121 SGK Toán lớp 9 Tập 2: Cắt một hình trụ hoặc một hình cầu bởi mặt phẳng vuông góc với trục, ta được hình gì ? Hãy điền vào bảng (chỉ với các từ “có”, “không”) (h.104).

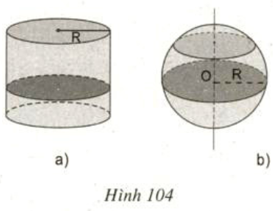
Lời giải:

Bài tập (trang 124; 125)

Bài 30 trang 124 SGK Toán lớp 9 Tập 2: Nếu thể tích của một hình cầu là $113\frac{1}{7}c{m}^3$ thì trong các kết quả sau đây, kết quả nào là bán kính của nó, lấy  $\pi \approx \frac{22}{7}$?

(A) 2cm;              

(B) 3cm;              

(C) 5cm;              

(D) 6cm;

(E) Một kết quả khác.

Lời giải:

 Ta có công thức tính thể tích của hình cầu:

$V=\frac{4}{3}\pi R^3\Rightarrow R^3=\frac{3V}{4\pi }$

Mà theo đề bài ta có:

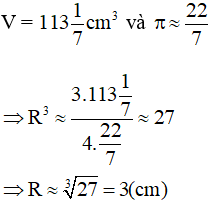
Vậy ta chọn đáp án (B)

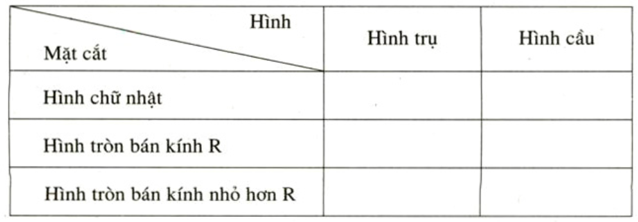
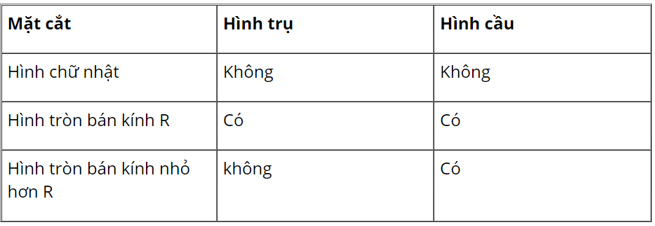
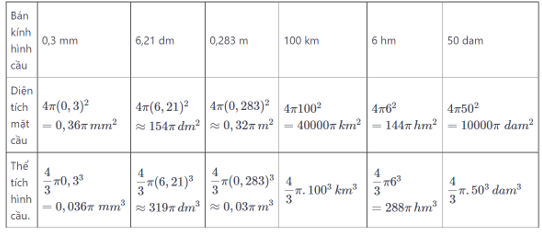
Bài 31 trang 124 SGK Toán lớp 9 Tập 2:Hãy điền vào ô trống ở bảng sau:

Lời giải:

Áp dụng các công thức:

Cho hình cầu có bán kính là R

Ta có:

Diện tích mặt cầu: $S=4\pi R^2=\pi d^2$

Thể tích hình cầu: $V=\frac{4}{3}\pi R^3=\frac{1}{6}\pi d^3$

Bài 32 trang 125 SGK Toán lớp 9 Tập 2:Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị :cm). Người ta khoét rỗng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).

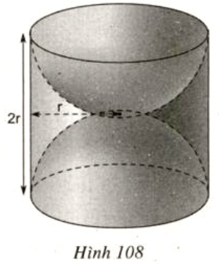
Lời giải:

Diện tích bề mặt khối gỗ bao gồm diện tích xung quanh của hình trụ và diện tích 2 nửa hình cầu.

Diện tích xung quanh của hình trụ là:

 $S_{xq}=2\pi rh=2\pi r.2r$$=4\pi r^2\left(c{m}^2\right)$

Diện tích một mặt cầu là: $S=4\pi r^2$

Diện tích bề mặt của khối gỗ là:

 $$\begin{gathered} S_{xq}+2\frac{S}{2}=S_{xq}+S \\ =4\pi r^2+4\pi r^2=8\pi r^2\left(c{m}^2\right) \end{gathered}$$

Bài 33 trang 125 SGK Toán lớp 9 Tập 2: Dụng cụ thể thao. Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đến chữ số thập phân thứ hai):

Lời giải:

Áp dụng các công thức:

Cho hình cầu có bán kính là R

Ta có:

Đường kính: d = 2R

Độ dài đường tròn lớn: $C=2\pi R=\pi d$

Diện tích mặt cầu: $S=4\pi R^2=\pi d^2$

Thể tích hình cầu: $V=\frac{4}{3}\pi R^3=\frac{1}{6}\pi d^3$

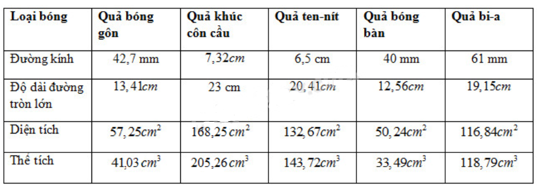
Bài 34 trang 125 SGK Toán lớp 9 Tập 2: Khinh khí cầu của nhà Mông - gôn - fi - ê (Montgolfier).

Ngày 4 - 6 - 1783, anh em nhà Mông-gôn-fi-ê (người Pháp) phát minh ra khinh khí cầu dùng không khí nóng. Coi khinh khí cầu này là hình cầu có đường kính 11m. Hãy tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải:

Diện tích của khinh khí cầu hình cầu có đường kính 11m là:

$$\begin{gathered} S=4\pi r^2=\pi d^2=\pi {11}^2 \\ \approx 379,94\left(m^2\right) \end{gathered}$$

Luyện tập trang 126

Bài 35 trang 126 SGK Toán lớp 9 Tập 2: Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (h.110). Hãy tính thể tích của bồn chứa theo các kích thước cho trên hình vẽ.

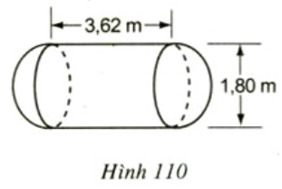
Lời giải:

Thể tích cần tính gồm một hình trụ và một hình cầu

Bán kính đáy của hình trụ là: r =  $\frac{1,8}{2}=0,9$ (m)

Chiều cao của hình trụ là: h = 3,62m

Bài 36 trang 126 SGK Toán lớp 9 Tập 2: Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm).

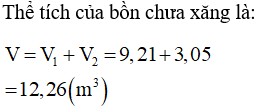
a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi và bằng 2a.

b) Với điều kiện ở a), hãy tính diện tích bề mặt và thể tích của chi tiết máy theo x và a.

Lời giải:

a)

Đặt AO = O’A’ = a

Ta có: AA’ = AO + OO’ + O’A’

 $\Rightarrow$2a = x + h + x

$\Rightarrow$ h + 2x = 2a

b)

Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính là x, chiều cao là h và diện tích mặt cầu có bán kính là x.

Diện tích xung quanh của hình trụ là: $S_t=2\pi xh$

Diện tích mặt cầu: $S_c=4\pi x^2$

Diện tích bề mặt của chi tiết máy là:

$$\begin{gathered} S=S_t+S_c \\ =2\pi xh+4\pi x^2=2\pi x(h+2x) \end{gathered}$$

Mà: h + 2x = 2a  (chứng minh phần a)

$\Rightarrow S=4\pi ax$

Thể tích cần tìm gồm thể tích hình trụ và thể tích một hình cầu.

Thể tích hình trụ là:

$V_t=\pi x^{2}h$

Thể tích hình cầu là:

$V_c=\frac{4}{3}\pi x^3$

Thể tích của chi tiết máy là:

$V=V_t+V_c=\pi x^{2}h+\frac{4}{3}\pi x^3$

Mà: h + 2x = 2a  (chứng minh phần a)

Bài 37 trang 126 SGK Toán lớp 9 Tập 2: Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.

a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.

b) Chứng minh $AM.BN=R^2$.

c) Tính tỉ số $\frac{S_{MON}}{S_{APB}}$ khi $AM=\frac{R}{2}$.

d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.

Lời giải:

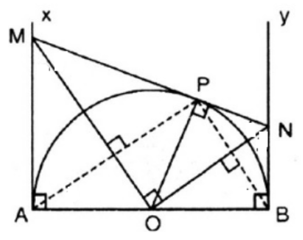
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).

Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.

Vậy tam giác MON vuông tại O.

Góc APB là góc nội tiếp chắn nửa đường tròn nên $\widehat{APB}={90}^o$

Do AM là tiếp tuyến với (O) tại A nên $\widehat{MAO}={90}^o$

Do MN là tiếp tuyến với (O) tại P nên $\widehat{MPO}={90}^o$

Tứ giác AOPM có:

$$\begin{gathered} \widehat{MAO}+\widehat{MPO}={90}^o+{90}^o \\ ={180}^o \end{gathered}$$

Do đó, tứ giác AOPM nội tiếp đường tròn

$\Rightarrow \widehat{POM}=\widehat{PAO}$ (do là hai góc nội tiếp chắn cung OP)

Xét tam giác MON và tam giác APB  có:

$\widehat{MON}=\widehat{APB}={90}^o$ (chứng minh trên)

$\widehat{POM}=\widehat{PAO}$ (chứng minh trên)

Do đó, tam giác MON đồng dạng với tam giác APB (góc – góc)

b) Tam giác MON vuông tại O có đường cao OP

Áp dụng hệ thức lượng trong tam giác ta có: $O{P}^2=MP.NP$ (1)

Theo tính chất hai tiếp tuyến MN và AM cắt nhau ta có:

MA = MP (2)

Theo tính chất hai tiếp tuyến MN và BN cắt nhau ta có:

NP = NB (3)

Theo (1), (2) và (3) ta có: $O{P}^2=MA.NB\Rightarrow R^2=MA.NB$ (đcpcm)

c) Theo phần a, tam giác MON và tam giác APB đồng dạng với nhau

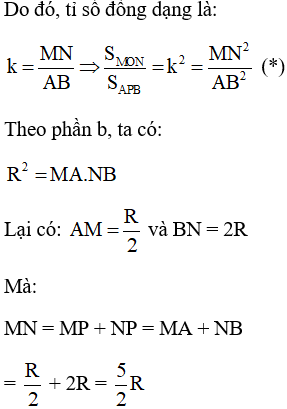
Nên:

$M{N}^2={\left(\frac{5}{2}R\right)}^2=\frac{25R^2}{4}$  và AB = 2R

Thay vào (*) ta có: $\frac{S_{MON}}{S_{APB}}=\frac{M{N}^2}{A{B}^2}=\frac{\frac{25R^2}{4}}{{\left(2R\right)}^2}=\frac{25}{16}$

d) Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R nên thể tích khối cầu tạo ra là: $V=\frac{4}{3}\pi R^3$.