Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 4 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 4 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu. Mời các bạn đón xem:
Bài tập Toán 9 Chương 4 Bài 3:Hình cầu. Diện tích mặt cầu và thể tích hình cầu
A. Bài tập Hình cầu. Diện tích mặt cầu và thể tích hình cầu
I. Bài tập trắc nghiệm
Câu 1: Cho hình cầu có đường kính d = 6cm. Diện tích mặt cầu là:
A. 36π (cm2)
B. 9π (cm2)
C. 12π (cm2)
D. 36π (cm2)
Chọn đáp án A.
Câu 2: Cho mặt cầu có thể tích V = 288π (cm3). Tính đường kính mặt cầu:
A. 6cm
B. 12cm
C. 8cm
D. 16cm
Chọn đáp án B.
Câu 3: Cho mặt cầu có số đo diện tích bằng số đo thể tích. Tính bán kính mặt cầu:
A. 3
B. 6
C. 9
D. 12
Lời giải:
Từ giả thiết ta có:
Chọn đáp án A.
Câu 4: Cho hình cầu có bán kính 3cm. Một hình nón cũng có bán kính đáy bằng 3cm và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón:
A. 3
B. 6√3
C. 72
D. 6√2
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
Chọn đáp án D.
Câu 5: Cho hình cầu có diện tích mặt cầu là 64π (cm2). Tính thể tích khối cầu?
Ta có:
Chọn đáp án A.
Câu 6: Cho hình cầu có thể tích là: 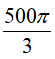
A. 50π (cm2)
B. 100π (cm2)
C. 25π (cm2)
D. 75π (cm2)
Ta có:
Chọn đáp án B.
Câu 7: Cho hình nón có bán kính đáy là 4cm và chiều cao 6cm. Thể tích của một hình cầu bằng thể tích hình nón. Tính bán kính hình cầu?
Lời giải:
Chọn đáp án C.
Câu 8: Cho một hình trụ có bán kính đường tròn đáy là 3cm và chiều cao h = 4cm. Một hình cầu có diện tích bằng diện tích xung quang của hình trụ. Tính bán kính của hình cầu?
A. R = 3cm
B. R = 2cm
C. R = √3 cm
D. R = √6 cm
Chọn đáp án D.
Câu 9: Cho hình trụ có bán kính đáy là 4cm . Một hình cầu có diện tích mặt cầu bằng diện tích hai đáy của hình trụ.Tính bán kính hình cầu?
A. R = 3cm
B. R = 4cm
C. R = 2√2 cm
D. R = 3√2 cm
Chọn đáp án C.
Câu 10: Một hình cầu có thể tích là 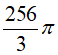
A. 32π
B. 16π
C. 48π
D. 64π
Chọn đáp án D.
Câu 11: Cho một hình cầu nội tiếp trong hình trụ. Biết rằng đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên h = 2R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ
Đáp án cần chọn là: A
Câu 12: Cho một hình cầu nội tiếp trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy bà bán kính đáy hình trụ bằng bán kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ
Từ đề bài suy ra chiều cao của hình trụ là h = 3R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ
Đáp án cần chọn là: B
Câu 13: Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình lập phương
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu R = 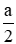
Khi đó ta có diện tích mặt cầu
Diện tích toàn phần của hình lập phương Stp = 6a2
Tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình lập phương là
Đáp án cần chọn là: C
Câu 14: Cho một hình cầu và một hình lập phương ngoại tiếp nó.Nếu diện tích toàn phần của hình lập phương là 24cm2 thì diện tích mặt cầu là:
A. 4π
B. 4
C. 2π
D. 2
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu R = 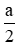
Diện tích toàn phần của hình lập phương Stp = 6a2 = 24 ⇔ a = 2cm
Khi đó ta có diện tích mặt cầu S = 4πR2 = 4π.12 = 4π (cm2)
Đáp án cần chọn là: A
Câu 15: Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a. Tính diện tích mặt cầu được tạo thành khi quay nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC
Vì tam giác ABC vuông tại A nên có đường tròn ngoại tiếp là đường tròn đường kính BC
Bán kính đường tròn ngoại tiếp tam giác là
Theo định lý Pytago ta có BC2 = AB2 + AC2 = 2a2
Khi quay nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC ta được hình cầu có bán kính 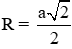
Đáp án cần chọn là: A
II. Bài tập tự luận có lời giải
Câu 1: Một hình cầu có số đo diện tích mặt cầu (tính bằng ) đúng bằng số đo thể tích của nó (tính bằng ). Tính bán kính của hình cầu đó.
Lời giải:
Câu 2: Tính bán kính của một mặt cầu, biết rằng mặt cầu đó có số đo đại số diện tích bằng số đo thể tích
Lời giải:
Theo bài ra ta có: 4/3.π.R3 = 4πR3 ⇔ R/3 = 1 ⇔ R = 3 (đơn vị độ đài)
Vậy bán kính mặt cầu là 3
III. Bài tập vân dụng
Câu 1: Khi bán kính của một mặt cầu tăng lên 3/2 lần thì diện tích và thể tích thay đổi như thế nào?
Câu 2: Giả sử trái cam có hình tương tự như mặt cầu, bạn Lan cắt trái cam làm đôi và tiến hành đo đường kính của nửa trái cam vừa cắt, bạn đo được bán kính tính cả vỏ cam là 2,5cm, biết vỏ cam dày 3mm. Hãy tính thể tích thực của quả cam đó.
B. Lý thuyết Hình cầu. Diện tích mặt cầu và thể tích hình cầu
1. Hình cầu
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.
- Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.
- Điểm O được gọi tâm, R là bán kính của hình cầu hay mặt cầu đó.
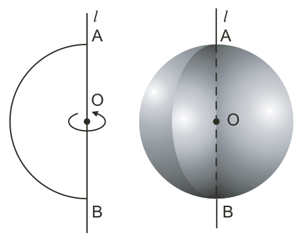
2. Cắt hình cầu bởi một mặt phẳng
Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn.
Ví dụ 1. Mặt phẳng (P) cắt hình cầu tâm O, bán kính R ta được hình tròn như hình vẽ.
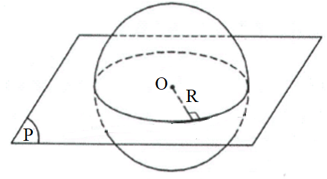
Khi cắt mặt cầu bán kính R bởi một mặt phẳng ta được một đường tròn:
- Đường tròn đó có bán kính R nếu mặt phẳng đi qua tâm (gọi là đường tròn lớn).
- Đường tròn đó có bán kính bé hơn R nếu mặt phẳng không đi qua tâm.
Ví dụ 2. Khi cắt mặt cầu tâm O bán kính R bởi một mặt phẳng ta được:
- Đường tròn tâm O bán kính R: mặt phẳng đi qua tâm.
- Đường tròn tâm O’ bán kính R’: mặt phẳng không đi qua tâm.
Ta có hình vẽ:
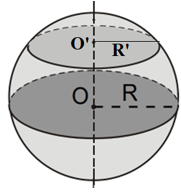
3. Diện tích và thể tích của hình cầu

Ví dụ 3. Một hình cầu có thể tích bằng 972π cm3. Tính diện tích của mặt cầu đó.
Lời giải:
Bán kính của mặt cầu đó là:
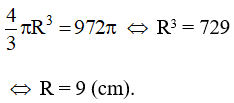
Diện tích của mặt cầu đó là:
S = 4πR2 = 4π . 92 = 324π (cm2)
Vậy diện tích của mặt cầu đó là 324π cm2.