Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 5: Phương trình chứa ẩn ở mẫu hay, chi tiết giúp học sinh dễ dàng làm bài tập Phương trình chứa ẩn ở mẫu lớp 8.

Giải bài tập Toán lớp 8 Bài 5: Phương trình chứa ẩn ở mẫu

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 19 Toán 8 Tập 2: Giá trị x = 1 có phải là nghiệm của phương trình hay không ? Vì sao?

Lời giải

Giá trị x = 1 không phải là nghiệm của phương trình.

Vì tại x = 1 thì $\frac{1}{x-1}$  có mẫu bằng 0,vô lí.

Câu hỏi 2 trang 20 Toán 8 Tập 2: Tìm điều kiện xác định của mỗi phương trình sau:

$a)\frac{x}{x-1}=\frac{x+\text{\hspace{0.17em}\hspace{0.17em}}4}{x+1}$;

$b)\frac{3}{x-2}=\frac{2x-1}{x-2}-x$.

Lời giải

a) Phương trình $\frac{x}{x-1}=\frac{x+\text{\hspace{0.17em}\hspace{0.17em}}4}{x+1}$  xác định:

$\left\{\begin{array}{c}x-1\ne 0\\ x+\text{\hspace{0.17em}}1\ne 0\end{array}\right.\iff \left\{\begin{array}{c}x\ne 1\\ x\ne -1\end{array}\right.$

Vậy ĐKXĐ của phương trình là x ≠ ±1.

b) Phương trình  $\frac{3}{x-2}=\frac{2x-1}{x-2}-x$xác định khi:

x – 2 ≠ 0 khi x ≠ 2

Vậy ĐKXĐ của phương trình là x ≠ 2.

Câu hỏi 3 trang 22 Toán 8 Tập 2: Giải các phương trình trong câu hỏi 2

Lời giải

$a)\frac{x}{x-1}=\frac{x+\text{\hspace{0.17em}\hspace{0.17em}}4}{x+1}$;

Điều kiện xác định: $x\ne \pm 1$

$$\begin{gathered} \frac{x}{x-1}=\frac{x+\text{\hspace{0.17em}\hspace{0.17em}}4}{x+1} \\ \iff \frac{x(x+\text{}1)}{(x-1)(x+1)}=\frac{(x-1)(x+\text{}4)}{(x+1)(x-1)} \end{gathered}$$

Suy ra x(x + 1) = (x - 1)(x + 4)

Ta có:

x(x + 1) = (x - 1)(x + 4)

⇔ x² + x = x² + 4x - x – 4

$$\begin{gathered} \iff x^2+x-x^2-4x+x+4=0 \\ \iff \left(x^2-x^2\right)+\left(x-4x+x\right)+4=0 \\ \iff -2x+4=0 \end{gathered}$$

⇔ 2x = 4

⇔ x = 2 (thỏa mãn ĐKXĐ)

Vậy tập nghiệm của phương trình là : S = {2}

b) Điều kiện xác định : x ≠ 2 .

$$\begin{gathered} \frac{3}{x-2}=\frac{2x-1}{x-2}-x \\ \iff \frac{3}{x-2}=\frac{2x-1}{x-2}-\frac{x(x-2)}{x-2} \end{gathered}$$

Suy ra 3 = 2x - 1 - x(x - 2)

⇔ 3 = 2x – 1 - (x² - 2x)

⇔ 3 = 2x - 1 - x² + 2x

⇔ 3 = 4x - 1 - x²

⇔ x² – 4x + 4 = 0

⇔ (x - 2)² = 0

⇔ x - 2= 0

⇔ x = 2 ( không thỏa mãn ĐKXĐ)

Vậy tập nghiệm của phương trình là : S = ∅

Bài tập (trang 22; 23)

Bài 27 trang 22 Toán 8 Tập 2: Giải các phương trình:

a) $\frac{2x-5}{x+5}=3$;

b) $\frac{x^2-6}{x}=x+\text{\hspace{0.17em}}\frac{3}{2}$;

c) $\frac{(x^2+\text{}2x)-(3x+\text{\hspace{0.17em}}6)}{x-3}=0$;

d) $\frac{5}{3x+\text{\hspace{0.17em}}2}=2x-1$.

Lời giải:

a) Điều kiện xác định: x ≠ -5.

$$\begin{gathered} \frac{2x-5}{x+5}=3 \\ \iff \frac{2x-5}{x+5}=\frac{3(x+\text{\hspace{0.17em}}5)}{x+5} \end{gathered}$$

Suy ra: 2x – 5 = 3(x + 5)

⇔ 2x – 5 = 3x + 15

⇔ 2x – 3x = 15 + 5                                 

⇔ -x = 20 nên x = -20 (thỏa mãn điều kiện xác định).

Vậy phương trình có tập nghiệm S = {-20}.

b) Điều kiện xác định: x ≠ 0.

$$\begin{gathered} \frac{x^2-6}{x}=x+\text{\hspace{0.17em}}\frac{3}{2} \\ \iff \frac{2(x^2-6)}{2x}=\text{\hspace{0.17em}}\frac{2x^2+\text{\hspace{0.17em}}3x}{2x} \end{gathered}$$

Suy ra: 2(x² – 6) = 2x² + 3x

⇔ 2x² – 12 – 2x² – 3x = 0

⇔ - 12 - 3x = 0

⇔ -3x = 12

⇔ x = -4 (thỏa mãn điều kiện xác định)

Vậy phương trình có tập nghiệm S = {-4}.

c) Điều kiện xác định: x ≠ 3.

$\frac{(x^2+\text{}2x)-(3x+\text{\hspace{0.17em}}6)}{x-3}=0$;

Suy ra: (x² + 2x) – (3x + 6) = 0

⇔ x(x + 2) – 3(x + 2) = 0

⇔ (x – 3)(x + 2) = 0

⇔ x – 3 = 0 hoặc x + 2 = 0

+ Nếu x – 3 = 0 ⇔ x = 3 (Không thỏa mãn đkxđ)

+ Nếu  x + 2 = 0 ⇔ x = -2 (Thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-2}.

d) Điều kiện xác định: $x\ne -\frac{2}{3}$ 

$\frac{5}{3x+\text{\hspace{0.17em}}2}=2x-1$.

$\iff \frac{5}{3x+\text{\hspace{0.17em}}2}=\frac{(2x-1).(3x+2)}{3x+2}$

Suy ra: 5 = (2x – 1)(3x + 2) hay (2x – 1)(3x + 2) = 5

⇔ 2x.3x + 2x.2 – 1.3x – 1.2 = 5

⇔ 6x² + 4x – 3x – 2 – 5 = 0

⇔ 6x² + x – 7 = 0.

⇔ 6x² – 6x + 7x – 7 = 0 (Tách để phân tích vế trái thành nhân tử)

⇔ 6x(x – 1) + 7(x – 1) = 0

⇔ (6x + 7)(x – 1) = 0

⇔ 6x + 7 = 0 hoặc x – 1 = 0

+Nếu 6x + 7 = 0 ⇔ 6x = - 7 ⇔ $x=\frac{-7}{6}$  (thỏa mãn đkxđ)

+Nếu x – 1 = 0 ⇔ x = 1 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm $S=\left\{-\frac{7}{6};1\right\}$ .

Bài 28 trang 22 Toán 8 Tập 2: Giải các phương trình:

a) $\frac{2x-1}{x-1}\text{\hspace{0.17em}\hspace{0.17em}}+1=\frac{1}{x-1}$ ;

b) $\frac{5x}{2x+\text{}2}+1=\frac{-6}{x+\text{\hspace{0.17em}}1}$;

c) $x+\frac{1}{x}=x^2+\frac{1}{x^2}$;

d) $\frac{x+\text{\hspace{0.17em}}3}{x+\text{\hspace{0.17em}\hspace{0.17em}}1}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{x-2}{x}=2$.

Lời giải:

a) Điều kiện xác định: x ≠ 1.

$$\begin{gathered} \frac{2x-1}{x-1}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}1=\frac{1}{x-1} \\ \iff \frac{2x-1+1(x-1)\text{}}{x-1}\text{\hspace{0.17em}\hspace{0.17em}}=\frac{1}{x-1} \end{gathered}$$

Suy ra: 2x – 1 + x – 1 = 1

⇔ 3x – 2 = 1

⇔ 3x = 3

⇔ x = 1 (không thỏa mãn điều kiện xác định).

Vậy phương trình vô nghiệm.

b) Điều kiện xác định: x ≠ -1.

$$\begin{gathered} \frac{5x}{2x+2}+1=\frac{-6}{x+\text{\hspace{0.17em}}1} \\ \iff \frac{5x}{2\left(x+1\right)}+\frac{2\left(x+1\right)}{2\left(x+1\right)}=\frac{\left(-6\right).2}{2\left(x+1\right)} \\ \iff \frac{5x+\text{\hspace{0.17em}\hspace{0.17em}}2(x+1)}{2(x+1)}=\frac{-6.2}{2(x+\text{\hspace{0.17em}}1)} \end{gathered}$$

Suy ra: 5x + 2(x + 1) = -12

⇔ 5x + 2x + 2 = -12

⇔ 7x + 2 = -12

⇔ 7x = -14

⇔ x = -2 (thỏa mãn đkxđ)

Vậy phương trình có tập nghiệm S = {-2}

c) Điều kiện xác định: x ≠ 0.

$x+\frac{1}{x}=x^2+\frac{1}{x^2}$  ;

$\iff \frac{x^3+\text{\hspace{0.17em}}x}{x^2}=\frac{x^4+\text{\hspace{0.17em}\hspace{0.17em}}1}{x^2}$

Suy ra: x³ + x = x⁴ + 1

⇔ x⁴ + 1 – x – x³ = 0

⇔ (x⁴ – x³) + (1 – x) = 0

⇔ x³(x – 1) – (x – 1) = 0

⇔ (x³ – 1)(x – 1) = 0

⇔ (x – 1)(x² + x + 1)(x – 1) = 0

⇔ (x – 1)². (x² + x + 1) = 0

⇔ x – 1 = 0

(vì $x^2+x+1=x^2\text{}+x+\frac{1}{4}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{3}{4}$$\hspace{0.17em}={\left(x+\frac{1}{2}\right)}^2+\text{\hspace{0.17em}\hspace{0.17em}}\frac{3}{4}>0\forall x$ ).

⇔ x = 1 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {1}.

d) Điều kiện xác định: x ≠ 0 và x ≠ -1.

$$\begin{gathered} \frac{x+\text{\hspace{0.17em}}3}{x+\text{\hspace{0.17em}\hspace{0.17em}}1}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{x-2}{x}=2 \\ \iff \frac{(x+\text{\hspace{0.17em}}3).x}{(x+\text{\hspace{0.17em}\hspace{0.17em}}1).x}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{(x-2)(x+1)}{x(x+\text{}1)}=\frac{2x(x+1)}{x(x+1)} \end{gathered}$$

Suy ra: (x + 3)x + (x - 2)(x + 1) = 2.x(x + 1)

⇔ x(x + 3) + (x + 1)(x – 2) – 2x(x + 1) = 0

⇔ x² + 3x + x² – 2x + x – 2 – (2x² + 2x) = 0

⇔ x² + 3x + x² – 2x + x – 2 – 2x² - 2x = 0

⇔ (x² + x² – 2x²) + (3x + x – 2x – 2x) – 2 = 0

⇔ 0x – 2 = 0

⇔ 0x = 2 vô lí

Vậy phương trình vô nghiệm.

Bài 29 trang 22-23 Toán 8 Tập 2: Bạn Sơn giải phương trình

$\frac{x^2-5x}{x-5}=5$ (1) như sau:

(1)⇔ x² – 5x = 5(x – 5)

⇔ x² – 5x = 5x – 25

⇔ x² – 10x + 25 =0

⇔ (x - 5)² = 0

⇔ x = 5

Bạn Hà cho rằng Sơn giải sai vì đã nhân hai vế với biểu thức x – 5 có chứa ẩn. Hà giải bằng cách rút gọn vế trái như sau:

$\left(1\right)\iff \frac{x(x-5)}{x-5}=5\iff x=5$

Hãy cho biết ý kiến của em về hai lời giải trên.

Lời giải:

+) Cách làm của bạn Sơn sai vì chưa đặt điều kiện xác định cho phương trình đã nhân cả hai vế với ( x- 5).

+) Cách làm của bạn Hà sai vì chưa đặt điều kiện xác định cho phương trình đã rút gọn cả hai vế cho biểu thức (x- 5) phụ thuộc biến x.

+) Cách giải đúng

Điều kiện xác định: x ≠ 5

Ta có: $\frac{x^2-5x}{x-5}=5$

$\iff \frac{x^2-5x}{x-5}=\frac{5(x-5)}{x-5}$

Suy ra: x² – 5x = 5( x - 5)

⇔ x( x - 5) – 5(x – 5) = 0

⇔ ( x - 5).( x - 5) =0

⇔ (x - 5)² = 0

⇔ x – 5= 0

⇔ x = 5 ( không thỏa mãn ĐKXĐ).

Vậy phương trình đã cho vô nghiệm.

Bài 30 trang 23 Toán 8 Tập 2: Giải các phương trình:

a) $\frac{1}{x-2}+3=\frac{x-3}{2-x}$;

b) $2x-\frac{2x^2}{x+\text{\hspace{0.17em}}3}=\frac{4x}{x+\text{\hspace{0.17em}}3}+\text{\hspace{0.17em}}\frac{2}{7}$;

c) $\frac{x+\text{\hspace{0.17em}}1}{x-1}-\frac{x-1}{x+\text{\hspace{0.17em}}1}=\frac{4}{x^2-1}$;

d) $\frac{3x-2}{x+\text{\hspace{0.17em}}7}=\frac{6x+1}{2x-3}$.

Lời giải:

a) Điều kiện xác định: x ≠ 2.

$\frac{1}{x-2}+3=\frac{x-3}{2-x}$

$\iff \frac{1+3(x-2)}{x-2}=\frac{-(x-3)}{x-2}$

Suy ra: 1 + 3(x – 2) = -(x – 3)

⇔ 1 + 3x – 6 = -x + 3

⇔ 3x + x = 3 + 6 – 1

⇔ 4x = 8

⇔ x = 2 (không thỏa mãn đkxđ).

Vậy phương trình vô nghiệm.

b) Điều kiện xác định: x ≠ -3.

$$\begin{gathered} 2x-\frac{2x^2}{x+\text{\hspace{0.17em}}3}=\frac{4x}{x+\text{\hspace{0.17em}}3}+\text{\hspace{0.17em}}\frac{2}{7} \\ \iff \frac{7.2x(x+3)-7.2x^2}{7(x+\text{\hspace{0.17em}}3)}=\frac{7.4x}{7.(x+\text{\hspace{0.17em}}3)}+\text{\hspace{0.17em}}\frac{2(x+3)}{7(x+3)} \end{gathered}$$

Suy ra: 14x(x + 3) – 14x² = 28x + 2(x + 3)

⇔ 14x² + 42x – 14x² = 28x + 2x + 6

⇔ 42x – 28x – 2x = 6

⇔ 12x = 6

⇔ x =  $\frac{1}{2}$(thỏa mãn điều kiện)

Vậy phương trình có tập nghiệm S = $\left\{\frac{1}{2}\right\}$.

c) Điều kiện xác định: x ≠ ±1.

  $\frac{x+\text{\hspace{0.17em}}1}{x-1}-\frac{x-1}{x+1}=\frac{4}{x^2-1}$;

$\iff \frac{(x+\text{\hspace{0.17em}}1)(x+1)}{(x-1)(x+1)}-\frac{(x-1)(x-1)}{(x+\text{\hspace{0.17em}}1)(x-1)}=\frac{4}{(x+1)(x-1)}$

Suy ra: x² + 2x + 1 – (x² – 2x + 1) = 4

⇔ x² + 2x + 1 – x² + 2x – 1 = 4

⇔ 4x = 4

⇔ x = 1 (không thỏa mãn đkxđ)

Vậy phương trình vô nghiệm.

d) Điều kiện xác định: x ≠ -7; x ≠ $\frac{3}{2}$.

$$\begin{gathered} \frac{3x-2}{x+\text{\hspace{0.17em}}7}=\frac{6x+1}{2x-3} \\ \iff \frac{(3x-2)(2x-3)}{(x+\text{\hspace{0.17em}}7)(2x-3)}=\frac{(6x+1)(x+7)}{(2x-3)(x+7)} \end{gathered}$$

Suy ra: (3x – 2)(2x – 3) = (6x + 1)(x + 7)

⇔ 6x² – 9x – 4x + 6 = 6x² + 42x + x + 7

⇔ - 4x - 9x - 42x - x = 7 - 6

⇔ - 56x = 1

⇔ x =  $\frac{-1}{56}$(thỏa mãn đkxđ)

Vậy phương trình có tập nghiệm S = $\left\{\frac{-1}{56}\right\}$ .

Bài 31 trang 23 Toán 8 Tập 2: Giải các phương trình:

Lời giải:

a) + Tìm điều kiện xác định :

x² + x + 1 = $\left(x^2+x+\frac{1}{4}\right) +\frac{3}{4}$

$\hspace{0.17em}={\left(x+\text{\hspace{0.17em}}\frac{1}{2}\right)}^2+\frac{3}{4}>0$  với mọi x ∈ R.

Do đó x² + x + 1 ≠ 0 với mọi x ∈ .

x³ – 1 ≠ 0 ⇔ (x – 1)(x² + x + 1) ≠ 0 ⇔ x – 1 ≠ 0 ⇔ x ≠ 1.

Vậy điều kiện xác định của phương trình là x ≠ 1.

+ Giải phương trình:

⇒ x² + x + 1 – 3x² = 2x(x – 1)

⇔ -2x² + x + 1 = 2x² – 2x

⇔ -4x² + 3x + 1 = 0

⇔ -4x² + 4x - x + 1 = 0

⇔ -4x(x – 1) – ( x – 1) = 0

⇔ (-4x - 1)(x – 1) = 0

⇔ - 4x - 1 = 0 hoặc x – 1 = 0

+) Nếu - 4x - 1 = 0 ⇔ - 4x = 1 ⇔ x = $\frac{-1}{4}$ (thỏa mãn đkxđ)

+) Nếu x – 1 = 0 ⇔ x = 1 (không thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = $\left\{\frac{-1}{4}\right\}$.

b) Điều kiện xác định: x ≠ 1; x ≠ 2; x ≠ 3.

⇒ 3(x – 3) + 2(x – 2) = x – 1

⇔ 3x – 9 + 2x – 4 = x – 1

⇔ 3x + 2x – x = 9 + 4 – 1

⇔ 4x = 12

⇔ x = 3 (không thỏa mãn điều kiện xác định)

Vậy phương trình vô nghiệm.

c)

+) Ta có: 8 + x³ = (2 + x).( 4 - 2x+ x² )

Mà 4 - 2x + x² = (1 – 2x + x² ) + 3 = (1- x)² + 3 > 0 với mọi x.

Do đó: 8 + x³ ≠ 0 ⇔ 2 + x ≠ 0 ⇔ x ≠ -2

+) Điều kiện xác định: x ≠ -2.

⇔ (2 + x). (4 – 2x + x²) + 4 – 2x + x² = 12

⇔ 8 + x³ + 4 – 2x + x² – 12 = 0

⇔ x³ + x² – 2x = 0

⇔ x(x² + x – 2) =0

Do đó, x = 0 hoặc x² + x – 2 = 0.

Giải phương trình x² + x – 2 = 0.

⇔ x² – 1 + x – 1 = 0.

⇔ (x + 1)(x - 1) + 1(x - 1) = 0

⇔(x - 1)(x + 1 + 1) = 0

⇔(x - 1)(x + 2) = 0

⇔ x – 1 = 0 hoặc x + 2 = 0

Nếu x – 1 = 0 thì x = 1.

Nếu x + 2 = 0 thì x = -2.

Kết hợp với điều kiện, vậy tập nghiệm của phương trình là S = {0; 1}.

d) Điều kiện xác định: x ≠ ±3; x ≠ $\frac{-7}{2}$ .

⇒ 13(x + 3) + (x – 3)(x + 3) = 6(2x + 7)

⇔ 13x + 39 + x² – 9 = 12x + 42

⇔ x² + x – 12 = 0

⇔ x² + 4x – 3x – 12 = 0

⇔ x(x + 4) – 3(x + 4) = 0

⇔ (x – 3)(x + 4) = 0

⇔ x – 3 = 0 hoặc x + 4 = 0

Nếu x – 3 = 0 ⇔ x = 3 (không thỏa mãn đkxđ)

Nếu x + 4 = 0 ⇔ x = -4 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-4}.

Bài 32 trang 23 Toán 8 Tập 2: Giải các phương trình:

a) $\frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2=\left(\frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2\right)(x^2+\text{\hspace{0.17em}}1)$;

b) ${\left(x+\text{\hspace{0.17em}\hspace{0.17em}}1+\text{\hspace{0.17em}}\frac{1}{x}\right)}^2={\left(x-1-\frac{1}{x}\right)}^2$.

Lời giải:

a) ĐKXĐ: $x\ne 0$

$$\begin{gathered} \frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2=\left(\frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2\right)(x^2+\text{\hspace{0.17em}}1) \\ \iff \frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2-\left(\frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2\right)(x^2+\text{\hspace{0.17em}}1)=0 \\ \iff \left(\frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2\right)(1-x^2-\text{\hspace{0.17em}}1)=0 \\ \iff \left(\frac{1}{x}\text{\hspace{0.17em}\hspace{0.17em}}+2\right)(-x^2)=0 \\ \iff \left[\begin{array}{c}\frac{1}{x}\text{\hspace{0.17em}}+2=0\\ -x^2=0\end{array}\right. \\ \iff \left[\begin{array}{c}\frac{1}{x}=-2\\ x^2=0\end{array}\right. \\ \iff \left[\begin{array}{c}x=\frac{-1}{2}\\ x=0\end{array}\right. \end{gathered}$$

Kết hợp điều kiện, vậy phương trình có nghiệm duy nhất $x=\frac{-1}{2}$.

b) ${\left(x+\text{\hspace{0.17em}\hspace{0.17em}}1+\text{\hspace{0.17em}}\frac{1}{x}\right)}^2={\left(x-1-\frac{1}{x}\right)}^2$

ĐKXĐ: $x\ne 0$.

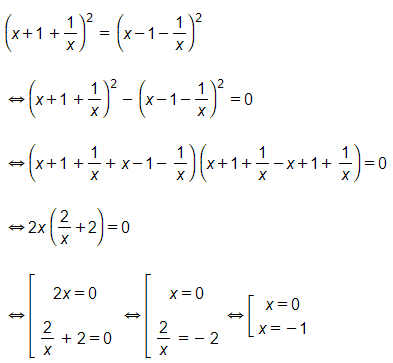
Kết hợp điều kiện, nghiệm của phương trình là x = -1.

Bài 33 trang 23 Toán 8 Tập 2: Tìm các giá trị của a sao cho mỗi biểu thức sau có giá trị bằng 2:

a) $\frac{3a-1}{3a+\text{\hspace{0.17em}}1}+\frac{a-3}{a+3}$ ;

b) $\frac{10}{3}-\frac{3a-1}{4a+\text{\hspace{0.17em}\hspace{0.17em}}12}-\frac{7a+\text{\hspace{0.17em}}2}{6a+18}$.

Lời giải:

a) Biểu thức có giá trị bằng 2 thì:

$\frac{3a-1}{3a+\text{\hspace{0.17em}}1}+\frac{a-3}{a+3}=2$

ĐKXĐ: $a\ne -3;a\ne \frac{-1}{3}$.

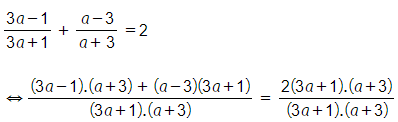
Suy ra: (3a – 1).(a + 3) + (a – 3)(3a + 1) = 2(3a + 1). (a + 3)

$\iff$3a² + 9a – a – 3 + 3a² + a – 9a – 3 = 2(3a² + 9a + a + 3)

$\iff$6a² – 6 = 6a² + 18a + 2a + 6

$\iff$6a² – 6 - 6a² - 18a - 2a – 6  = 0

$\iff$-20a – 12 = 0

 $\iff$-20a = 12

$\iff a=\frac{-3}{5}$( thỏa mãn điều kiện)

Vậy với $a=\frac{-3}{5}$ thì biểu thức đã cho có giá trị 2.

b) Để biểu thức có giá trị bằng 2 thì $\frac{10}{3}-\frac{3a-1}{4a+\text{\hspace{0.17em}\hspace{0.17em}}12}-\frac{7a+\text{\hspace{0.17em}}2}{6a+18}=2$

ĐKXĐ: $a\ne -3$

Ta có:

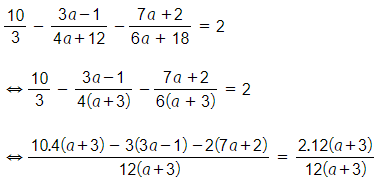
Suy ra: 10.4(a + 3) – 3(3a – 1) – 2.(7a + 2) = 2.12(a + 3)

$\iff$40a + 120 – 9a + 3 – 14a – 4 = 24a + 72

$\iff$17a + 119 = 24a + 72

$\iff$17a – 24a = 72 - 119

$\iff$-7a = - 47

$\iff a=\frac{47}{7}$ (thỏa mãn điều kiện)

Vậy với $\iff a=\frac{47}{7}$thì biểu thức đã cho có giá trị bằng 2.